高等數學課程思政教學改革的探索與實踐

褚蕾蕾

（西安交通大學數學與統計學院，陜西 西安 710049）

0 引言

2020年6月1日，教育部頒發了《高等學校課程思政建設指導綱要》[1]，提出了課程思政建設是全面提高人才培養質量的重要任務。高數教學實施“課程思政”是一種新的教學改革指向，也是借助高數課程進行思政教育的實踐活動，其目標是以“立德樹人”為高等數學課程教學的根本任務。“育人為本、德育為先”，將社會主義核心價值觀作為課程教學指向，在高等數學課程思政案例中融入政治認同、國家意識、文化自信和公民人格的思政元素，并在高數課堂場景中將案例引入教學實踐，以建立滲透德智體美勞知識的教學體系，培養學生正確的世界觀、人生觀、價值觀。實現知識傳授、方法啟迪、價值引領與情感關懷的統一，將“三全育人”落實到高等數學的教學課程中。這就要求將課程思政融入課堂教學建設的全過程，要讓課程思政內容進人才培養方案、進教學大綱、進教案課件、進課堂、進考試，貫穿于教學的各環節，逐步提高課程思政內涵融入課堂教學的水平。教師是高數“課程思政”教學改革的主體，要以課程思政案例設計為抓手，恰當處理高等數學、思政課程、數學文化的關系，選用、設計教學案例，通過案例實現課程功能。

近年來，有學者對高數教學中滲透課程思政元素進行討論，如吳慧卓[2]，俞能福[3]等。本文在分析高等數學課程存在豐富思政元素的基礎上，提出了課程思政融入教學的一種設計方案，并給出教學實踐的調查。

1 高等數學課程中存在豐富的思政元素

在高等數學課程教學中，挖掘其思政元素，有如下六大方面可作為思政案例設計的參考。

1.1 微積分課程教學是我國建設工業強國的國家意識的體現

1671—1684年，牛頓和萊布尼茨分別從運動學與幾何學中直觀的無窮小量出發建立了微積分。隨后，1764—1782年，英國的詹姆斯·瓦特在格拉斯哥大學發明并改進了蒸汽機。人類從此進入了工業化時代，微積分學伴隨工業化的發展而發展。到20世紀50年代，微積分也是我國工業化的一個重要的數學基礎，全國理工科專業均開設高等數學的相關課程，體現了我國工業化的國家意識和對我國發展戰略的認同。今天，它仍然服務于我國的現代化建設，并增添了新的廣度和深度，這是開設與學習該課程的目的。

1.2 高等數學的本質是認識論問題

首先微積分的研究對象是實數域上連續函數的分析性質，是人們認識物質世界中一些具體事物的抽象，這種抽象概念是人的大腦心智活動，而不是既獨立于客觀世界又獨立于人類思想而存的一個實在，所以，討論微積分中的概念、理論和方法是一個認識論問題。其二，微積分學的發展是一個由經驗認識上升到理論知識的過程，有一個由觀察、歸納、算法到理論分析的過程，其過程不是從公理出發經邏輯推理而得，也就是說微積分是應用數學而不是純數學，盡管公理化方法在描述數學中有重要的應用。其三，既然這是一個應用型的認識論問題，它的源泉就只能是實際問題、實踐問題。其四，檢驗微積分真理性的唯一標準是實踐，作為一門數學理論，對它的真理性檢驗包括邏輯驗證、理論檢驗和應用驗證等三個方面。實踐是數學認識的源泉與數學真理性的檢驗標準。

1.3 微積分的基本特征是對立的統一

例如有許多重要的對立概念，如極限的存在性與不存在性，函數的連續性與不連續性，可微與不可微，可積與不可積，二重極限的可交換與不可交換等，其中最基本的是有窮與無窮的對立，在無窮的概念中有潛無窮與實無窮的觀點。無理數的發現、無窮小量的提出和實無窮集合論的提出，引起了數學的三次危機，也使其在對立中得以發展，有的還產生新的數學分支。

1.4 數學的無窮觀與無窮小量的存在性

在現代科學的描述中，人類所認識的宇宙是普朗克尺度（大約10-35米，10-44秒）上的有限宇宙，而現代數學又描繪了一個與有限物質宇宙完全不同的、無窮的數學世界。極少的數學家采取有窮主義的立場，而大多數則認為自然數是可以構造出來的，且可以一直作下去，這就是潛無窮的觀點。— 語言采用潛無窮的觀點避開無窮小量的術語建立了精確的極限表述。完備實數系建立在集合論的基礎上，是采用實無窮的觀點。這就產生了直覺主義學派與形式主義學派的分野。直到1960年前后，魯賓遜建立非標準實數域才解決了無窮小量的存在性問題，使其在哲學本體論的爭論上解決了貝克萊的詰難。高等數學滲透了數學哲學的基本問題。

1.5 數學的文化藝術特征

1872年由德國數學家維爾斯特拉斯構造的處處連續卻處處不可微函數，是分析中的重要反例，也是高等數學并不特別關注的“病態”函數。但是，這些反例卻成了分形幾何思想的源泉，后者提供了數學計算機藝術的分形圖形。它們反映出與數學和諧美的另一個奇異性的美感。前者如歐幾里得規矩美的和諧，后者如曼德勃羅特分形美的熱情奔放。分形就是從奇異中誕生的新穎，這是提升學生文化素養的優良素材。

1.6 數學家的創新精神和優秀品格

在數學的發展歷史中，有許多數學家表現出可貴的創新精神、科學素養與優秀的品格，他們積極進取、鍥而不舍的治學精神，獨立思考、富于創見的治學態度，值得我們學習。他們崇高的家國情懷和使命擔當，鼓舞和激勵著學生們奮勇前行。

2 高數課程思政的實踐探索

2.1 高數課程思政的案例設計

在高等數學思政案例設計中應秉承如下原則。首先要服務于高數課程思政的總任務，體現“品行養成、知識傳授、能力培養、思維創新”四位一體的人才培養理念。其二挖掘高數課程的思政元素，使高等數學與思想政治理論課同向同行。其三要注重高等數學“工具性、知識性、科學性、思想性、素養性、文化性”的基本要求，體現高等數學基本的思想方法。其四要選取學生易懂、教師熟悉、便于教學的案例，要有知識性、文化性，不生冷硬拗，有大眾化的知識拓展空間，能引起較為廣泛的興趣或深入的討論，同時設計案例的書寫要規范，以體現對案例的理解邏輯。

在案例設計中采用的模板，含案例名稱、主題、情景（結合章節、學情分析、教學安排、教學方法）、案例描述（基本描述、問題提出、知識拓展、元素融合）、思政元素及案例反思，后者是教師備課的注記。

2.2 高數課程思政的教學設計

設計六個高數思政案例，可制作為課件，穿插講授共四個課時，簡要介紹如下。

案例1：微積分的產生與思維模式。案例情景：緒論。思政元素：微積分產生于人類的社會實踐活動，創新地發明了一種無窮小分析的思維模式。實踐是認識的源泉，也是檢驗真理的標準。

案例2：割圓術與微積分的應用模式。案例情景：逼近的概念。思政元素：認識的過程是由感性認識上升到理性認識；《九章算術》反映了中華文化對數學研究模式的選擇，這種模型化、算法化的方法，也是高等數學解決實際問題的模式。

案例3：無窮小量的存在性與數學的無窮觀。案例情景：無窮小量的概念。思政元素：通過無窮小量存在性問題的解決，認識到對立統一規律是事物的普遍規律。在人的成長過程中不要懼怕矛盾，要敢于斗爭，善于斗爭，要有正確的方法去解決矛盾。

案例4：導數計算與數學機械化。案例情景：導數的符號計算。思政元素：通過我國數學家吳文俊在中國古代數學機械化與代數化思想的影響下提出“吳方法”，建立初等幾何證明機械化完整體系的實例，增強學生的科學精神與文化自信。

案例5：維爾斯特拉斯函數與數學的分形藝術美。案例情景：可微函數與連續函數的關系。思政元素：數學的藝術美源于數學實踐，其形式美依賴于人類生產力的水平；學習科學家的品格與人文精神。

案例6：定積分概念的導入、微元法與數學的認識論方法。案例情景：定積分的概念和微元法。思政元素：通過定積分概念導入中的“分、均、合、精”方法，以及微元法的應用，強調實踐對數學方法論的重要性。說明在數學方法上存在演繹、歸納和類比等方法。歸納法也是人工智能的一種方法，歸納與直覺是一種創新性思維。

2.3 高數課程一個思政案例的簡要設計

下面給出課程思政案例四“導數計算與數學機械化”的簡要設計。通過導數計算的導引，引入數學證明機械化的工具──符號計算軟件。機器證明又稱自動推理，其基本思想是用一個固定的算法程式去解決一類問題，屬于人工智能的領域。初等幾何的機械化證明是數學證明機械化的重要例子。1976年底我國數學家吳文俊在中國古代數學機械化與代數化思想的影響下，提出了現稱為“吳方法”的奠基性論文[4]，隨后又建立了一套求解代數方程組的理論與方法，是求解代數方程組精確解最完整的方法之一，并實現于當前流行的符號計算軟件包中。1983年，吳方法被介紹到世界上，并于1997年獲得Herbrand自動推理杰出成就獎[5]。吳文俊曾獲得2000年首屆國家最高科技獎、1956年首屆國家自然科學一等獎，體現了崇高的家國情懷和使命擔當。

下面，簡述吳文俊一個建立初等幾何證明機械化的實例。其要點簡述如下。

例1用機械化方法證明“平行四邊形的兩條對角線互相平分”。

Step1將問題表示為代數式。設平行四邊形ABCD在平面上的位置如圖1所示。其對角線 AC與BD相交于Q。設各點坐標為：

圖1

A(0，0)，B(p，0)，C(u，v)，D(x，y)，Q(z，w).

將所設條件用坐標的代數等式來表示。條件DC//AB表示為

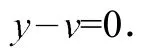
條件AD//BC表示為

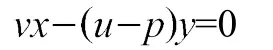
條件點Q在AC上表示為

條件點Q在BD上表示為

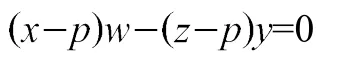
Step2將z、w作為未知量，求解上兩式組成的代數方程組，得

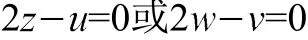
即證明結論|AQ|＝|QC|。由此可得

即結論|BQ|＝|QD|成立，完成該命題的證明。

吳方法給兩千多年的公理化演繹體系帶來了強烈沖擊，到20世紀80年代，吳文俊不僅建立了數學機械化證明的基礎，而且擴張成廣泛的數學機械化綱領，解決了一系列理論及實際問題。吳文俊積極進取、鍥而不舍的治學精神,獨立思考,富于創見的治學態度，是數學工作者的楷模，是中國數學界的一面旗幟。

2.4 對初步實施高數課程思政的評估

高等數學是大學數學課程及許多專業課程的基礎，我校每年有二十多個班同時進行周期一年的教學，面寬量大，內容繁重，是課程思政的一個重要戰場。

在今年電類大班的高數教學中初步引入思政案例，調查顯示在學生普遍感到課業壓力大的情況下，要創新課堂教學模式，關注學生思想動態。學生對課程中增加思政內容是抱有積極態度的，認可品德教育融入高數課程的必要性。將課程思政融入高等數學課，寓價值觀引導于知識傳授和能力培養之中，起到了幫助學生塑造正確的世界觀、人生觀和價值觀的作用，提高了學生正確認識問題、分析問題和解決問題的能力。在潛移默化中堅定了學生的理想信念，培養了學生探索未知、追求真理、勇攀科學高峰的責任感和使命感，激發了學生的民族文化自信，科技報國的家國情懷和使命擔當。從開展課程思政以來，明顯看到班上學習風氣的改變，擦黑板不用老師催促，上課遲到和打瞌睡的少了，課間打游戲的沒有了，學生之間談論的多數是與學業相關的問題。在和學生的談話中，感受到滿滿的正能量，并沒有因為課程思政占用了一部分教學時間而影響教學質量。師生互動增多，學生的作業質量和答疑狀況比之前都有明顯改善，學習成績也提高了，所以課程思政對高數課程的教學發揮了良好的促進作用。

3 結語

本文在高等數學教學改革中，通過思政元素挖掘、案例設計、課程設計、課件制作等過程進行高數課程思政建設，既是將課程思政融入高數教學的教學，體現“品行養成、知識傳授、能力培養、思維創新”四位一體的人才培養理念，又是教師進行課程思政建設的實踐性活動，有利于促進教師專業的發展。