客貨共線鐵路彈性支承塊式無砟軌道結構極限狀態設計法研究

陳 瀟

(中鐵第四勘察設計院集團有限公司,武漢 430063)

基于可靠度理論的極限狀態設計法已經成為國際工程結構設計的主流方法[1-2]。我國鐵路工程設計方法正在從容許應力法向極限狀態法轉換[3-5]，鐵路軌道自2011年起開展了系列研究課題和試設計工作[6-7]，于2018年正式發布Q/CR 9130—2018《鐵路軌道設計規范(極限狀態法)》[8]。然而，前期研究工作主要針對高速鐵路典型無砟軌道結構型式，如CRTSⅠ、Ⅱ、Ⅲ型板式及雙塊式無砟軌道[9-10]，缺乏對客貨共線鐵路彈性支承塊式無砟軌道極限狀態設計法的充分研究[11]。客貨共線鐵路等級、運營條件及軌道類型與“轉軌”研究對象不同，急需對客貨共線彈性支承塊式無砟軌道極限狀態設計方法進行研究。

以設計速度160 km/h客貨共線鐵路為對象，結合彈性支承塊式無砟軌道結構特點，分析彈性支承塊式無砟軌道結構計算模型和加載方式，提出彈性支承塊式無砟軌道極限狀態設計表達式及分項系數，并結合衢寧鐵路彈性支承塊式無砟軌道結構進行道床板極限狀態法試設計。

1 計算模型與加載方式

以客貨共線Ⅰ級鐵路、設計速度160 km/h、運營貨車軸重25 t為對象，隧道內彈性支承塊式無砟軌道由鋼軌、預埋鐵座式彈性可調扣件、預制混凝支承塊、支承塊下彈性墊板、橡膠套靴及道床板等組成，軌道結構高度為600 mm，如圖1所示。

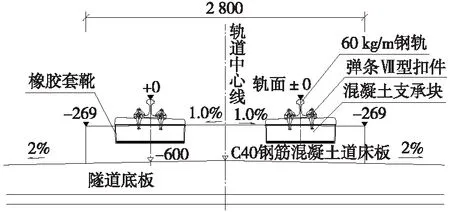
圖1 隧道內彈性支承塊式無砟軌道結構斷面示意(單位：mm)

彈性支承塊式無砟軌道結構區別于高速鐵路CRTSⅠ、Ⅱ、Ⅲ型板式及雙塊式無砟軌道的特點主要是低剛度和可修復性[12-13]。彈性支承塊式無砟軌道結構垂直彈性由軌下和塊下雙層彈性橡膠墊板提供；橡膠套靴則提供了軌道的縱、橫向彈性變形，使這種無砟軌道在承載、動力傳遞和振動能量吸收方面接近堅實均勻基礎上的碎石道床軌道。由于套靴的隔離作用，支承塊可從道床結構中取出，使運營中損傷的彈性支承塊系統具有可修復性。

Q/CR 930—2018《鐵路軌道設計規范(極限狀態法)》條文說明中規定：“列車豎向荷載引起的主體結構中的彎矩或應力，一般按‘彈性地基梁-板理論’進行計算”，對非板式軌道的模型和加載方式未明確。下文對模型是否考慮支承塊、橡膠套靴、墊板，以及加載方式進行分析。

1.1 計算模型

鋼軌采用60 kg/m、U75V無螺栓孔新鋼軌；扣件類型采用彈條Ⅶ型扣件，根據TJ/GW 152—2016《客貨共線鐵路隧道內彈性支承塊式無砟軌道用部件暫行技術條件》中規定，軌下墊板的靜剛度為100～120 kN/mm，動靜剛度比考慮為2.0；支承塊為C50混凝土結構；橡膠套靴剛度為200～300 kN/mm，塊下墊板剛度為60～90 kN/mm，動靜剛度比考慮為1.8；道床板分塊澆筑，板長為6.58 m，寬為2.8 m，采用C40混凝土現場澆筑。列車豎向荷載標準值Pk=2Pj，Pj為靜輪重，取設計靜軸重的一半，則Pk=250 kN。

分別建立不考慮和考慮支承塊結構模型，如圖2、圖3所示。

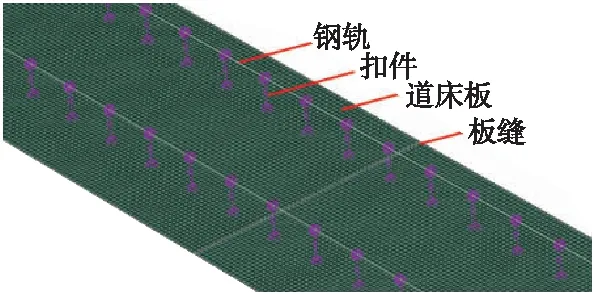
圖2 不考慮支承塊結構模型

圖3 考慮支承塊結構模型

加載方式采用單軸雙輪加載[14]，兩種計算模型的道床板彎矩結果如表1所示。

表1 道床板彎矩最大值 kN·m/m

由表1可知，不考慮支承塊模型計算所得的彎矩值明顯大于考慮支承塊模型的彎矩值：縱向最大正、負彎矩值分別增大2.68倍和1.01倍；橫向最大正、負彎矩值分別增大1.82倍和0.93倍；正彎矩增大更為明顯。

可見，支承塊結構(含橡膠套靴和塊下墊板)對列車荷載作用下道床板彎矩值影響較大，從而影響道床板的理論計算配筋結果，因此，建議在客貨共線鐵路軌道彈性支承塊式無砟軌道結構設計時，計算模型考慮支承塊、塊下墊板、橡膠套靴。

1.2 加載方式

加載方式考慮單軸雙輪、雙軸四輪(兩輪對間距2.5 m)、三軸六輪(輪對間距為2.5 m、2 m)3種加載方式，如圖4所示。根據列車荷載的作用位置，選取板中、板邊、板縫3種工況對模型進行計算，以便得到最不利加載位置的計算結果。

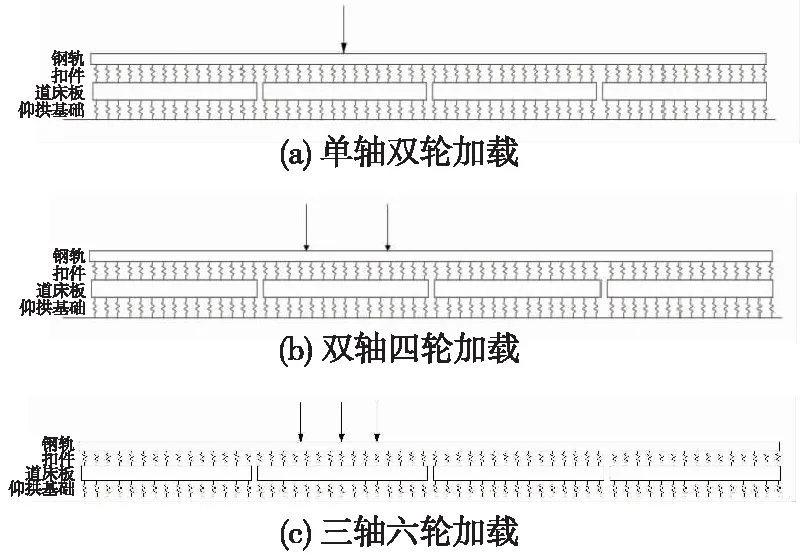
圖4 加載方式

根據計算結果，單軸雙輪、雙軸四輪和三軸六輪3種方式的最不利加載位置分別為板中、板邊和板縫，道床板彎矩結果見表2。

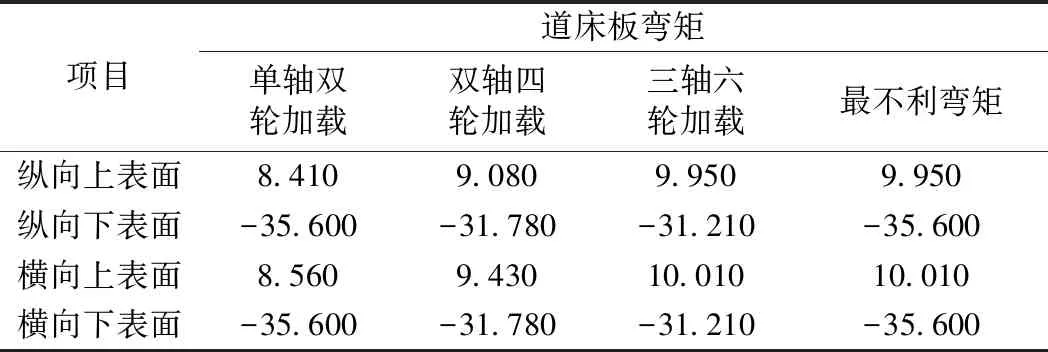
表2 不同加載方式道床板彎矩計算結果 kN·m/m

由表2可以看出，對于道床板板底正彎矩，隨著加載輪對增加，板底正彎矩有下降趨勢，列車荷載采用單軸雙輪加載且作用在板中時，板底正彎矩最大；對于道床板板頂負彎矩，隨著加載輪對增加，板頂負彎矩有上升降趨勢，列車荷載采用三軸六輪加載且作用在板縫時，板頂負彎矩最大。

2 極限狀態設計表達式及分項系數

2.1 功能函數

隧道內彈性支承塊式無砟軌道為單元結構，承載能力極限狀態為道床板正截面抗彎承載力滿足要求，正常使用極限狀態為最大道床板裂縫寬度滿足要求。

洞口小于200 m隧道內無砟軌道主要考慮列車荷載、溫度作用，洞口大于200 m隧道內無砟軌道僅考慮列車荷載。

道床板承載能力功能函數為

G(X)=MR-Md-Mt

(1)

式中，MR為道床板承載力的隨機變量；Md為道床板列車荷載作用效應的隨機變量；Mt為道床板溫度梯度作用效應的隨機變量。

正常使用功能函數為

G(X)=wlim-w

(2)

式中，wlim為道床板裂縫寬度限值；w為道床板計算裂縫寬度。

2.2 隨機變量概率模型及統計參數

(1)列車荷載效應

無砟軌道在列車荷載作用下的效應，按有限元計算確定。考慮列車輪載、扣件剛度、塊下墊板剛度、線下基礎剛度、道床板彈性模量為基本隨機變量(表3)，通過點估計有限元法[15]，采用立方正態分布來描述隨機參數下彈性支承塊式無砟軌道結構25 t軸重列車荷載效應統計特征，列車荷載作用下，道床板彎矩的前四階統計矩[16]如表4所示。

表3 基本隨機變量概率分布及統計特征參數

表4 列車荷載效應統計參數

(2)溫度梯度作用效應

根據前期轉軌研究對無砟軌道溫度梯度的觀測數據，其設計基準期的最大值分布為極值Ⅰ型分布，正溫度梯度變異系數為0.158，負溫度梯度變異系數為0.275。根據Q/CR 9130—2018《鐵路軌道設計規范(極限狀態法)》，最大正溫度梯度為90 ℃/m，最大負溫度梯度為45 ℃/m，板厚350 mm的修正系數為0.89，可求得最大正溫度梯度作用效應標準值90.92 kN·m/m，最大負溫度梯度作用效應標準值45.46 kN·m/m。

(3)抗力參數

結構抗力的概率分布及統計參數一般應根據其幾何參數制作出實體模型，并通過試驗確定。對于承載能力極限狀態的強度檢算，抗力也可以用彎矩來表示。對于純彎構件，最大可承受彎矩與鋼筋抗拉強度成正比，因而，最大可承受彎矩的變異系數可取為與鋼筋抗拉強度相同。根據鐵科院《鐵路工程結構極限狀態法設計關鍵抗力參數動態采集與分析》中的研究成果，HPB300、HRB400的力學性能統計分布建議值見表5。

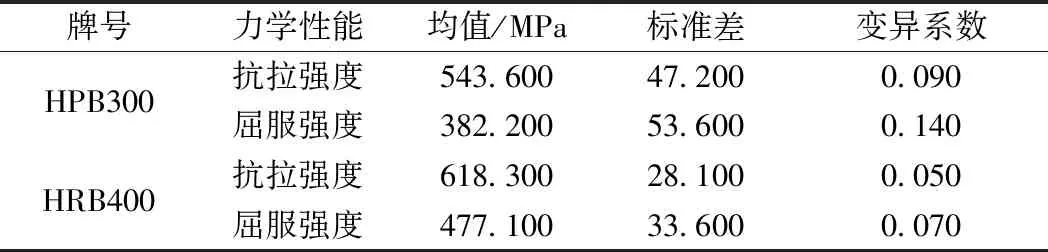
表5 鋼筋力學性能統計參數取值

2.3 道床板極限狀態法分項系數計算

以距隧道洞口小于200 m范圍彈性支承塊式無砟軌道道床板的極限狀態法設計為例，荷載效應考慮溫度梯度效應和列車作用效應。

(1)承載能力極限狀態法

客貨共線鐵路軌道彈性支承塊式無砟軌道道床板承載力極限狀態法設計表達式為

γdMdk+γtMtk≤φRMR

(3)

式中，γd，γt分別為列車荷載效應分項系數、溫度梯度作用效應分項系數；φR為道床板截面抵抗彎矩分項系數。對安全等級為二級的道床板進行極限狀態設計時，其承載能力極限狀態下的目標可靠指標為βT=3.7。

以道床板縱向正截面為例，采用極限狀態法進行設計并配置鋼筋，作用組合為列車荷載正彎矩效應+正溫度梯度作用效應。采用一次二階矩法[17]確定設計表達式中分項系數，計算求得的道床板分項系數設計表達式為

0.953MR≥1.161Mdk+0.47Mtk

(4)

(2)正常使用極限狀態

對道床板進行正常使用極限狀態(裂縫寬度不超過限值)設計時，功能函數為

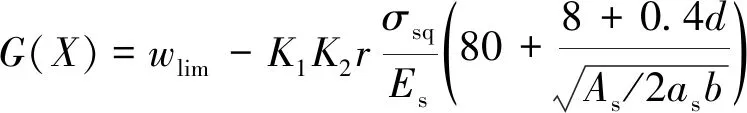
(5)

其中

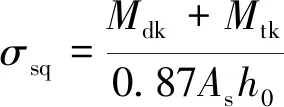
(6)

上式不能反映抵抗彎矩和作用彎矩效應的直接關系，但由于采用極限狀態法設計截面配筋時，保持道床板尺寸、混凝土等級及鋼筋種類不變，式中除受拉鋼筋面積與直徑以外的其他參數均已知(保護層厚度為35 mm，h0、as可根據截面高度與鋼筋直徑計算)，因此，將正常使用極限狀態方程等價于

G′(X)=f(As,d)-Mdk-Mtk≥0

(7)

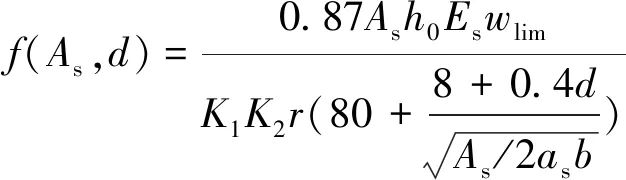
(8)

極限狀態法設計表達式為

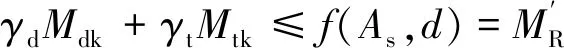
(9)

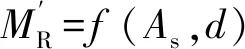
以道床板板底橫向裂縫寬度不超過限值的設計為例，采用極限狀態法進行設計并配置鋼筋，作用組合為常用列車荷載正彎矩效應+常用正溫度梯度作用效應。采用一次二階矩法確定設計表達式中分項系數，計算求得的道床板分項系數設計表達式及等效抵抗彎矩值為

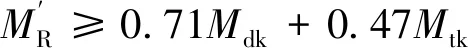
(10)

(3)道床板設計分項系數取值建議

由于規范設計表達式形式對結構抗力(即道床板承載力)不取分項系數，僅對作用效應取分項系數，因此，將上述分項系數表達式中MR的系數轉化為1，僅作用效應取分項系數。分別對道床板縱橫向上、下層分析極限狀態法設計分項系數，列于表6。

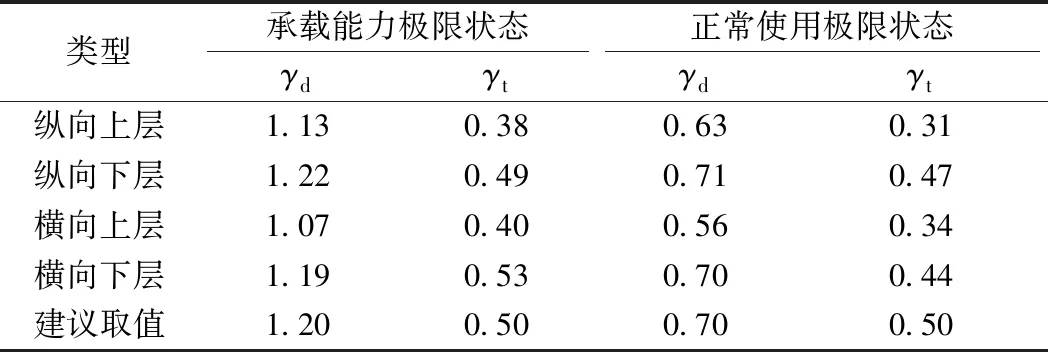
表6 道床板極限狀態法設計分項系數

3 極限狀態法試設計

以衢寧鐵路隧道內彈性支承塊式無砟軌道結構為對象，軌道結構如圖1所示，采用極限狀態法和容許應力法分別對其道床板進行配筋計算，道床板混凝土強度等級為C40，為分塊結構，寬2 800 mm，厚351 mm，采用HRB400級鋼筋。

隧道內彈性支承塊式無砟軌道為單元結構，承載能力極限狀態設計時，道床板按受彎構件進行正截面受彎承載力設計[19-20]；正常使用極限狀態設計時，道床板按受彎構件計算最大裂縫寬度。

3.1 距洞口小于200 m隧道地段

洞口小于200 m的隧道內無砟軌道主要考慮列車荷載、溫度作用，承載能力和正常使用極限狀態設計作用分項系數根據本文建議取值。道床板配筋計算結果如表7所示。

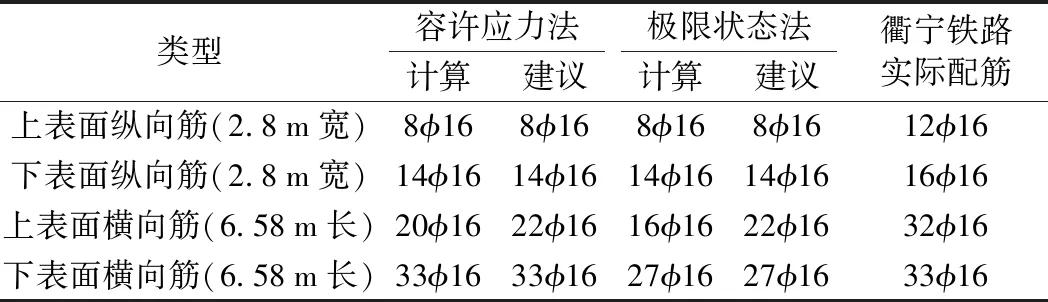
表7 計算配筋與衢寧鐵路配筋對比(距洞口小于200 m)

(1)理論計算配筋比較

對于隧道地段(距離洞口小于200 m)的彈性支承塊式無砟軌道道床板，極限狀態法計算的縱向配筋結果與容許應力法計算配筋一致；橫向上表面和下表面配筋分別減少4φ16 mm和6φ16 mm，減少20%和18%。

(2)建議配筋量比較

距洞口小于200 m隧道地段的彈性支承塊式無砟軌道道床板，考慮最小配筋率后，極限狀態法計算的縱向配筋結果與容許應力法計算配筋一致；橫向上表面和下表面配筋分別減少2φ16 mm和6φ16 mm，減少10%和18%。

采用極限狀態法建議的配筋與衢寧鐵路縱橫向鋼筋均減少，縱向鋼筋上下層分別減小4根、2根，橫向鋼筋上層減小10根、下層減少6根；采用容許應力法的建議配筋與衢寧鐵路縱橫向鋼筋均減少，縱向鋼筋上下層分別減小4根、2根，橫向鋼筋上層減小10根、下層相同。

3.2 距洞口大于200 m隧道地段

洞口大于200 m的隧道內無砟軌道僅考慮列車荷載，分項系數按本文建議取值。道床板配筋計算結果如表8所示。

表8 計算配筋與實際項目配筋對比(距洞口大于200 m)

(1)理論計算配筋比較

對于隧道地段(距離洞口大于200 m)的彈性支承塊式無砟軌道道床板，極限狀態法計算的縱橫向配筋結果比容許應力法計算配筋均有減少：縱向上表面和下表面配筋分別減少1φ16 mm和2φ16 mm，均減少30%；橫向上表面和下表面配筋分別減少1φ14 mm和3φ14 mm，減少14%和23%。

(2)建議配筋量比較

距洞口大于200 m隧道地段的彈性支承塊式無砟軌道道床板，考慮最小配筋率要求后，采用極限狀態法計算的縱橫向配筋與容許應力法一致，均為最小配筋率要求。

兩種方法建議配筋與衢寧鐵路實際配筋相比，縱向鋼筋上層減小3根、下層減少7根，橫向鋼筋上層減小8根、下層減少10根。

4 結論

結合客貨共線鐵路彈性支承塊式無砟軌道結構特點，分析了彈性支承塊式無砟軌道結構計算模型和加載方式，提出了彈性支承塊式無砟軌道極限狀態設計表達式及分項系數，并開展了道床板極限狀態法試設計，主要結論如下。

(1)建議在客貨共線鐵路彈性支承塊式無砟軌道結構設計時，采用考慮支承塊、塊下墊板、橡膠套靴的計算模型，加載方式采用最不利加載形式。

(2)對于距洞口小于200 m地段隧道內彈性支承塊式無砟軌道道床板，建議承載能力極限狀態下，列車荷載和溫度梯度作用分項系數分別取1.2、0.5，正常使用極限狀態下分別取0.7、0.5。

(3)采用極限狀態法對彈性支承塊無砟軌道結構道床板進行了配筋計算，距離洞口小于200 m地段道床板縱向配筋結果與容許應力法計算配筋一致；橫向上表面和下表面配筋分別減少2φ16 mm和6φ16 mm。