淺談協變類比思想在高三復習中的應用

重慶 楊天才

1 問題提出

高中物理涉及的思想方法很多，有整體與隔離、分割與積累、類比、降維、等效、極限、對稱、圖示與圖像、守恒、猜想與假設、數學物理方法，其中類比法也叫“比較類推法”“類比推理法”，是一種創造性的平行思維方法，也是研究物理問題常用的方法之一，對解決一些教學難點有至關重要的作用。類比是指根據兩類事物的部分特征相似，推出兩事物其他方面的特征也可能相似。類比對象間共有的屬性越多，則類比結論的可靠性越大，類比能夠使主體對已知事物的判斷直接過渡到對未知事物的判斷，其結論的正確性必須由實驗來檢驗。而協變類比是對象的屬性之間可能具有某種確定的函數關系而進行的推理，在高三復習過程中，很多不同板塊知識之間的內容有思維的共通性，完全可以用類比思維來解決難點，從而打破板塊之間的思維壁壘，使思想方法在這里融會貫通。本文以力學和電磁學中的協變類比為例進行探究。

2 協變類比

2.1 函數關系為(A、B、C為常數)

表1

2.2 函數關系為：(A、B為常數)

表2

3 應用舉例

【例1】類比是研究問題常用的方法

(2)情境2：如圖1所示，電源電動勢為E，導體棒的質量為m，定值電阻的阻值為R，忽略電源內阻及導體棒、軌道的電阻，整個裝置處于垂直于導軌向下的勻強磁場中，磁感應強度大小為B，間距為L的水平導軌光滑且足夠長。閉合開關S，導體棒開始加速運動，閉合開關瞬間開始計時。

圖1

a.求t=0時導體棒的加速度；

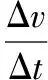
(3)情境3：如圖2所示，電源電動勢為E，線圈自感系數為L，電路中的總電阻為R。閉合開關S，發現電路中電流I隨時間t的變化規律與情境1中物體速率v隨時間t的變化規律類似。類比(Ⅰ)式，寫出電流I隨時間t變化的方程(Ⅲ)，并在圖3中定性畫出I-t圖像。

圖2

圖3

(5)類比情境1、情境2和情境3中的能量轉化情況，完成表3。

表3

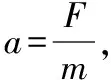
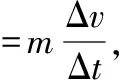
圖4

(5)由能量的轉化與守恒定律得

表4

【點評】本題考查協變類比思想的具體應用，對于電磁感應中速度隨時間、自感現象中電流隨時間變化的函數關系，對高中生來說較難，通過與雨滴下落類比，找到它們所滿足的方程的共同點，應用協變類比，使問題得以解決。教學中對一些難點的突破，對復雜問題的簡單處理，對物理規律的遷移，類比法都是很好的選擇。

【例2】類比是研究問題的常用方法

(1)情境1：如圖5所示，光滑水平面上的彈簧振子，鋼球質量為m、彈簧勁度系數為k，建立如圖6中所示的坐標軸。t=0時，將鋼球拉至x=A處由靜止釋放，小鋼球只在彈力作用下做往復運動，此過程中彈性勢能與鋼球動能相互轉化。求：

圖5

①t=0時刻小鋼球的加速度a；

圖6

(2)情境2：如圖7所示為LC振蕩電路，回路中電感線圈的自感系數為L，電容器的電容為C。如圖7所示，t=0時閉合開關，此時電容器兩極板所帶電荷量分別為+Q、-Q。忽略電磁輻射與回路電阻的熱損耗，此后LC電路自由振蕩。求t=0時刻電容器兩極板間的電勢差U。

圖7

(3)發現情境2中電容器極板的電荷量q隨時間t的變化規律與情境1中振子位移x隨時間t的變化規律類似。

①類比(Ⅰ)式，寫出電荷量q隨時間t的變化方程(Ⅱ)和對應的函數表達式。

②從開關S接2瞬間開始計時，在圖6所示的坐標系中定性畫出電容器上極板的電荷量q隨時間t變化的圖像，并求出LC振蕩電路的振蕩頻率f。

(4)質量是物體做機械運動時慣性大小的量度，在電磁現象中也存在“慣性”。在情境2中，哪個物理量可用來度量電磁“慣性”的大小。

【解析】(1)彈簧振子的位移x隨時間t變化的圖像如圖8所示。

圖8

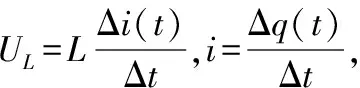
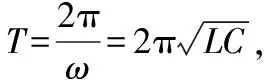
圖9

(4)在電磁現象中，物理量自感系數L可用來度量電磁“慣性”的大小。

【點評】電磁振蕩中電容器所帶電荷量、電容器極板間電壓、線圈中的感應電流隨時間的函數關系、振蕩頻率都是高中物理中不涉及推導的，但也是較難掌握的知識，用協變類比，可以大大降低思維難度，簡化思維過程，使學生達到“舉一反三”“觸類旁通”“活學活用”的目的。

4 結語