重力與萬有引力關系的模型建構與試題編制

福建 鄭行軍

萬有引力的試題編制是以萬有引力定律為基礎，融合圓周運動、重力、開普勒定律等進行綜合情境設計，對于學生的知識理解能力和空間想象能力都有較高的要求，其中萬有引力和重力的關系問題作為本章重要知識點之一，其理解深度與應用層次對問題的解決有較大影響。本文對兩者的關系及試題編制思路進行梳理，希望能對大家有所幫助。

一、重力與萬有引力關系的模型分析

1.地表且地球M(或某中心天體)自轉影響不能忽略

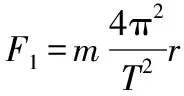
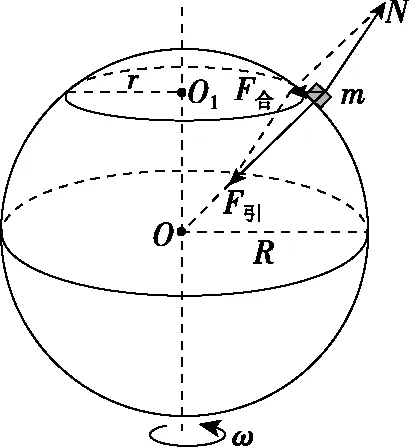
圖1

圖2

2.地球M(或某中心天體)上方高空

二、試題情境設計與編制

1.不同天體表面的重力加速度比較分析

設計思路：以兩個或多個不同天體為信息載體設計試題情境，構建地表重力與萬有引力的定量關系，作為核心考點拓展天體表面的重力加速度、天體質量、天體密度和環繞天體問題等，題設條件不涉及中心天體的自轉問題。

( )

2.同一天體不同高度的重力加速度比較分析

設計思路：聚焦同一中心天體作為參考載體，選擇高空不同位置或地表的兩個不同研究對象(實物或環繞天體)，通過重力與萬有引力關系式比較重力加速度關系，分析加速度、中心天體質量、密度、環繞問題等。

( )

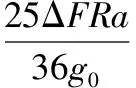
3.同一天體表面不同緯度的重力加速度比較分析

設計思路：在同一天體表面的不同緯度選擇兩個或多個不同位置做為重力加速度評測參考，不同地表位置的物體在研究受力關系時要考慮中心天體自轉的影響，結合重力加速度和向心力的動態關系分析重力加速度、向心力、向心加速度、地表支持力、自轉線速度、角速度等物理參量的變化或進行定量計算。

【例3】用彈簧測力計稱量一個相對于地球靜止的小物體的重量，隨稱量位置的變化可能會有不同的結果。已知地球質量為M，自轉周期為T，引力常量為G。將地球視為半徑為R、質量均勻分布的球體，不考慮空氣的影響。設在地球北極地面稱量時，彈簧測力計的讀數是F0。

圖3

4.天體內外不同位置的重力加速度比較分析

設計思路：以某一天體作為研究對象，在天體內部腔體、表面或高空選擇兩個或多個位置作為比較，分析不同位置的萬有引力或重力加速度關系等。

【例4】人類對自然的探索遠至遙遠的太空，深至地球內部。若地球半徑為R，把地球看作質量分布均勻的球體。某地下探測器A的質量為m，深入地面以下h處，假設h以上的地球球殼物質對探測器A的引力為零；另一太空探測器B質量也為m，圍繞地球做圓周運動，軌道距離地面高度為d，則地球對太空探測器B和地下探測器A的引力之比為

( )

圖4

5.地面或高空關聯物體的運動問題

設計思路：設計地面或高空的物體運動為試題情境，通過分析物體的運動規律，結合運動學、動力學、功能關系等力學知識，關聯出運動與天體表面或高空的加速度關系，延拓中心天體質量、密度、環繞天體的運動、變軌、發射問題等。

【例5】航天員飛到一個被稠密氣體包圍的某行星上進行科學探索。他站在該行星表面，從靜止釋放一個質量為m的物體，由于氣體阻力，其加速度a隨下落位移x變化的關系圖像如圖5所示。已知該星球半徑為R，引力常量為G，忽略行星自轉產生的影響。下列說法正確的是

圖5

( )

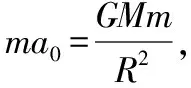
【點評】當運動涉及重力加速度的試題編制中，題目信息一般會呈現近地或高空的物體運動規律，如自由落體、豎直上拋、平拋、圓周運動等，并以此構建運動和重力加速度的關系，具體的試題特征是天體表面或高空的重力加速度一方面與天體有關[GM=gR2或GM=g′(R+h)2]；另一方面與物體運動關聯，利用重力加速度為紐帶建構物體運動和萬有引力、天體運動之間的關系(圖6)，因而可以實現地面和高空的有機統一，達到同時考查近地運動和高空天體作用規律的雙重目的，具有一定的綜合性。

圖6

三、小結