解決含定彈簧問題的“一圖五點二線”

甘肅 趙強強 李勝江

涉及彈簧的問題通常為綜合問題，物體運動過程復雜、涉及知識面廣、能力要求高，是許多學生望而生畏的題型。但是這類問題對培養學生的物理核心素養具有重要意義，可以有效完善學生的物理觀念，提升學生的科學思維和分析探究能力。現有的研究主要是對涉及彈簧的問題進行了分類討論，針對不同類型提出了不同的解決辦法，缺乏系統性，不利于學生物理思維的培養。彈簧產生彈力時的兩個端點都要連接物體，若彈簧某一端點的物體固定不動，則稱為定彈簧；若彈簧兩端連接的物體能同時運動，則稱為動彈簧。本文主要以定彈簧為例，展示“一圖五點二線”法解決含定彈簧類問題的策略。

1.構建“一圖五點二線”

1.1 一個彈簧形變過程圖

彈簧的形變可以沿任意方向，但高中階段只涉及沿彈簧軸線產生壓縮或拉伸形變時的問題，同時高中階段涉及的彈簧為輕彈簧，即不考慮自身重力的作用，彈簧產生形變的整個變化過程如圖1。圖中①②③④⑤為彈簧變化過程中的幾個特殊位置點，其中①②為壓縮狀態變化過程，④⑤為拉伸狀態變化過程。在彈簧產生形變的過程中，它的起點可以是任何一個點(通常為以上五個點中的某一個)，但變化過程只有兩個即從起點向序號數值變大方向變化或向序號數值變小方向變化，且變化一般發生在同一狀態(即壓縮狀態或拉伸狀態)，具體如圖1所示。

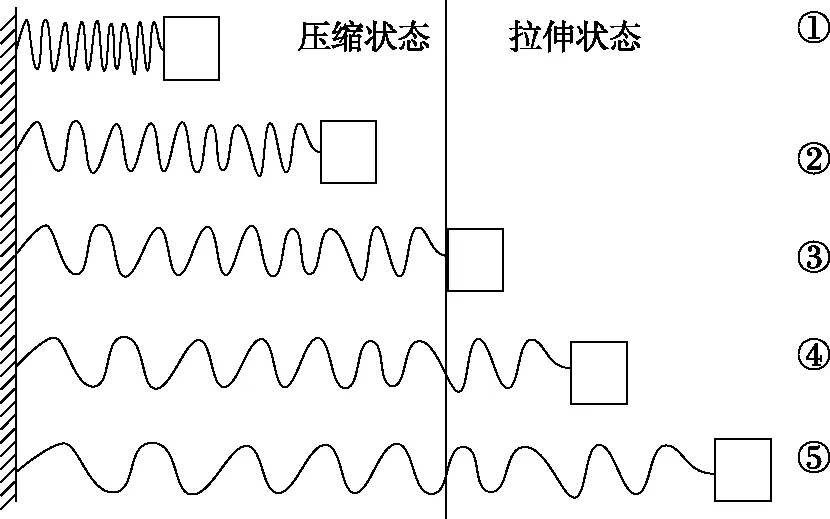
圖1 彈簧形變過程圖

1.2 五個特殊位置點

彈簧在產生形變的過程中，隨著形變量的變化，彈簧和彈簧連接物體的對應物理量也隨著改變，而在這個變化過程中彈簧在五個點時對應的各個物理量具有特殊性，總結如表1。為了分析方便，用F外表示物體受到的除彈簧彈力之外的其他力的合力，通常為一恒力、方向與彈簧彈力方向相反；F合表示物體受到的總合力；F、x、k分別表示彈簧產生的彈力、形變量和勁度系數；m、v和a分別表示與彈簧連接物體的質量、速度和加速度；Ep表示彈簧的彈性勢能，Ek表示與彈簧連接物體的動能，具體分析如表1。

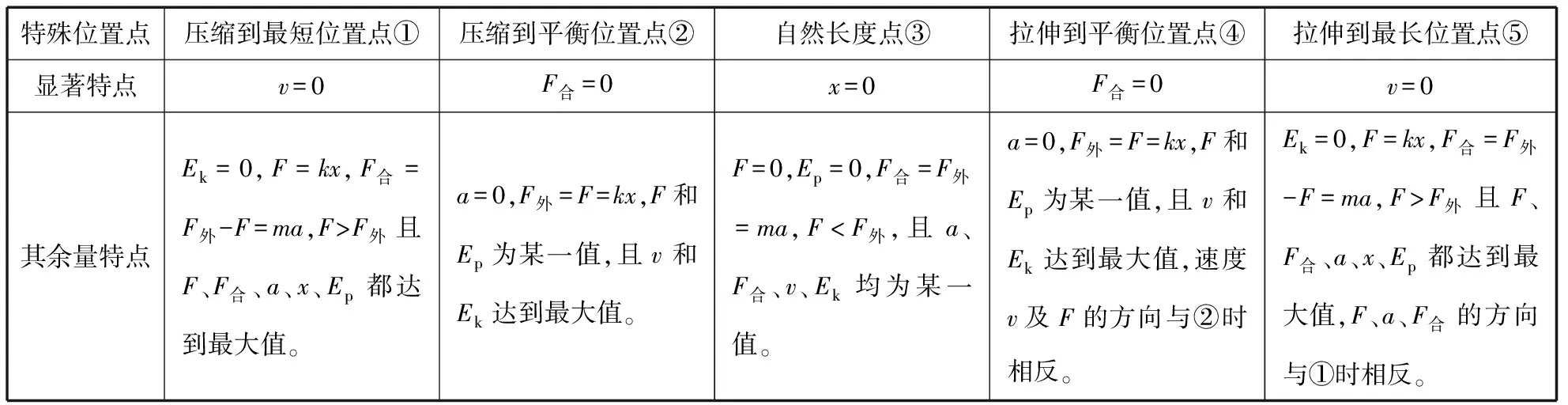
表1 五個特殊點對應物理量的特點

1.3 兩條變化主線

彈簧產生形變時的狀態有壓縮狀態和拉伸狀態，每個狀態又有兩條變化主線，分別為壓縮狀態的①→②→③和③→②→①過程及拉伸狀態的③→④→⑤和⑤→④→③過程，在不同狀態時物體所受彈簧彈力F反向。盡管彈簧的起點不同，但變化過程是固定的，可以從以上五個點的任一點開始沿著其中一條線變化，對照五個點的特點依次分析①→⑤和⑤→①對應的兩條變化過程表，如表2所示。

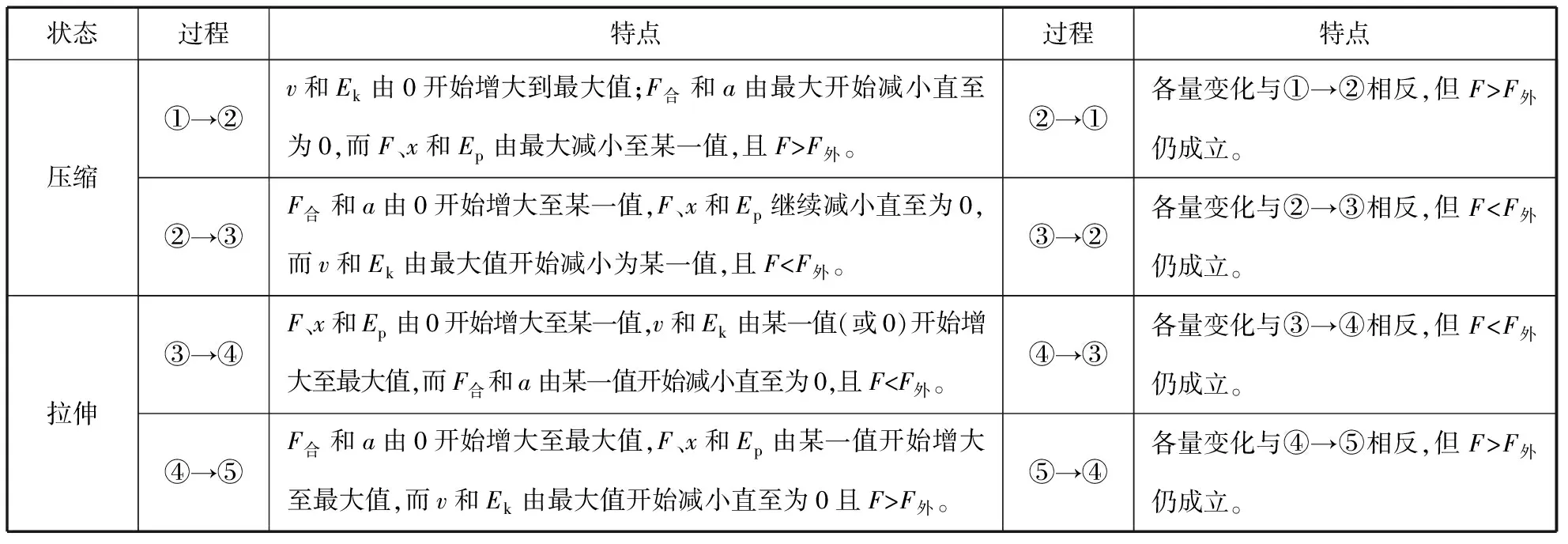
表2 兩條變化過程表

【總結】利用圖像將彈簧產生形變時兩個狀態對應的各個物理量隨形變量變化趨勢(非函數關系)反映出來，如圖2所示，橫軸x表示彈簧的形變量所對應的①②③④⑤五個特殊位置；線b表示v和Ek隨形變量x的變化趨勢，線c表示a和F合隨形變量x的變化趨勢，線d表示F和Ep隨形變量x的變化趨勢。

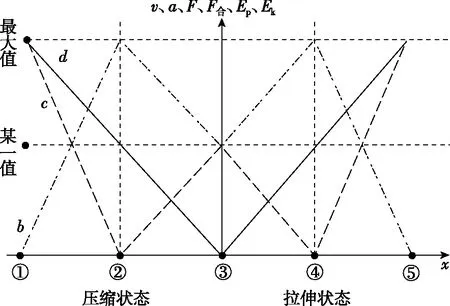
圖2 各物理量隨彈簧形變量的變化圖

2.“一圖五點二線”解題程序

含彈簧問題主要考查彈簧處在某一狀態時某些物理量的確定或者是某一變化過程中某些物理量的變化，同時還與連接彈簧的物體運動過程密切相關，因此利用“一圖五點二線”解決定彈簧問題時，可按以下流程，即定彈簧狀態(壓縮、拉伸或自然)→定彈簧特殊點(五個點中的其中一個或其他點)→定彈簧變化過程→定與彈簧連接物體的運動過程→定物體所受的外力F外→定物體所受的合力F合→定各物理量的關系式→定各物理量的變化。在這一流程中，可根據問題的實際情況確定分析的起點，中間某些過程也可以不出現，應靈活把握。

3.演繹“一圖五點二線”的解題過程

【例1】如圖3所示，輕彈簧豎直放置，下端固定在水平地面上，一質量為m的小球，從離彈簧上端高h處由靜止釋放，某同學在研究小球落到彈簧上后繼續向下運動到最低點的過程，他以小球開始下落的位置為原點，沿豎直向下方向建立坐標軸Ox作出小球所受彈力F的大小隨小球下落的位置坐標x變化的關系，如圖4所示，不計空氣阻力，重力加速度為g，以下判斷不正確的是

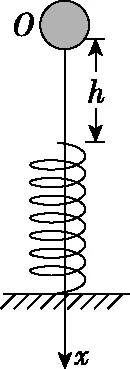
圖3

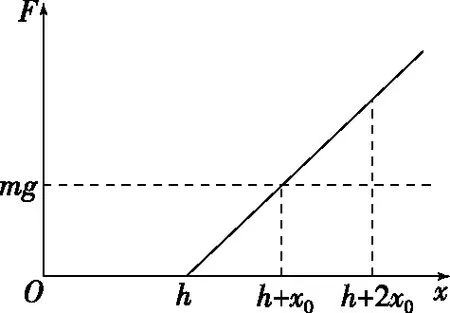
圖4

( )

A.當x=h+x0，小球的重力勢能與彈簧的彈性勢能之和最小

B.小球落到彈簧上向下運動到最低點的過程中，加速度先減小后增大

C.當x=h+2x0，小球的加速度大小為g

D.小球動能的最大值為mgh+mgx0

【答案】D

【解析】A選項：定彈簧狀態，當x=h+x0時，彈簧為壓縮狀態→定彈簧特殊點，x=h+x0對應特殊點②，F=kx0→定與彈簧連接物體的運動過程，小球豎直向下運動且速度達到最大，小球動能Ek達到最大→定物體所受的外力F外=mg→定物體所受的合力F合=0→定各物理量的關系式，由于彈簧和小球組成的系統機械能守恒，則Ek=EpG+Ep彈→定各物理量變化，小球的Ek最大，則小球的重力勢能與彈簧的彈性勢能之和EpG+Ep彈最小，故A正確。

B選項：定彈簧狀態，小球落到彈簧上向下運動到最低點的過程為彈簧壓縮狀態→定彈簧特殊點，剛落到彈簧上時對應特殊點③，F=0，F合=F外=ma；最低點對應特殊點①，F=2kx0，F合=F外=ma，a達到最大→定彈簧變化過程，對應③→②→①過程→定物體所受外力F外=mg→定各物理量變化，加速度a先減小后增大，故B正確。

C選項：定彈簧狀態，當x=h+2x0時彈簧為壓縮狀態→定彈簧特殊點，x=h+2x0對應特殊點①，F=2kx0，F合=F外=ma→定物體所受外力F外=mg→定物體所受合力F合=mg→定各物理量變化，此時a=g，故C正確。

D選項：定彈簧特殊點，小球動能最大時對應特殊點②→定與彈簧連接物體的運動過程，小球豎直向下運動且速度達到最大→定彈簧變化過程，對應③→②→①過程→定各物理量關系式，對小球由動能定理可得mg(h+x0)-W彈=Ekm-0→定各物理量變化，Ekm>mg(h+x0)，故D錯誤。

【例2】如圖5所示，重10 N的滑塊在傾角為30°的斜面上，從a點由靜止下滑，到b點接觸到一個輕彈簧。滑塊壓縮彈簧到c點開始彈回，返回b點離開彈簧，最后又回到a點，已知ab=0.8 m，bc=0.4 m，那么在整個過程中

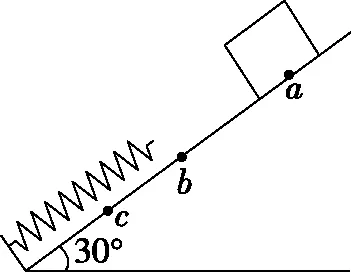
圖5

( )

A.滑塊動能的最大值是6 J

B.彈簧彈性勢能的最大值是6 J

C.從c到b彈簧的彈力對滑塊做的功是6 J

D.滑塊和彈簧組成的系統整個過程機械能減少

【答案】BC

【解析】滑塊從a點由靜止下滑到b點接觸彈簧后將彈簧壓縮到c點，返回b點離開彈簧，最高又回到a點，整個過程沒有能量損失，說明滑塊運動過程中不受摩擦力作用，滑塊和彈簧組成的系統整個過程機械能守恒，故D錯誤。

對C選項：定與彈簧連接物體的運動過程，沿斜面向下直至速度為0→定彈簧變化過程，對應③→②→①過程→定物體所受外力F外，對物體受力分析得F外=mgsinθ→定各物理量關系式，滑塊下滑到c過程由動能定理得0=W彈-mg(ab+bc)sinθ→定各物理量關系式，W彈=6 J，故C正確。

對B選項：定彈簧特殊點，彈簧彈性勢能的最大值對應特殊點①→定與彈簧連接物體的運動過程，對應滑塊在c點，由功能關系得Epm=W彈=6 J，故B正確。

對A選項：定彈簧特殊點，小球動能最大時對應特殊點②，設該點為b與c間的某一點d，F=kx，Ep為某一值→定與彈簧連接物體的運動過程，滑塊沿斜面向下運動速度達到最大，動能Ek達到最大→定彈簧變化過程，，對應③→②過程→定各物理量關系式，對滑塊下滑到最大動能過程，由能量守恒可得Ekm=mg(ab+bd)sinθ-Ep→定各物理量關系式，由于mg(ab+bc)sinθ=6 J，所以mg(ab+bd)sinθ<6 J，則Ekm<6 J，故A錯誤。

4.總結

彈簧最大的特點就是“可拉可壓”，并且在“拉”和“壓”時產生的彈力方向不同，導致物體的受力也產生變化，使得含彈簧問題比較復雜。涉及彈簧類問題在解題過程中要特別注意彈簧在產生形變過程中的特點，特別是五個特殊位置點，它們既反映彈簧的物理量特點，又反映與彈簧連接物體的運動特點，若將這些特點在分析解題過程中合理運用，就能達到事半功倍的效果。因此，教師在進行相關教學時，可以針對彈簧產生形變的過程先進行系統的分析，并采用圖像將形變過程直觀的呈現，再將形變過程中的五個特殊位置進行獨立的分析，找到各個物理量的特點，進而利用圖像將特殊點和形變過程組合起來，最后形成一個知識體系。總之，利用數形結合的思想方法可將復雜問題抽象為具體，簡化思路，降低思維難度，從而進一步培養學生分析處理物理問題的能力，提升學生的物理核心素養。