芻議初中數學解題中的模型思想

王沐蓉

(湖南工業大學理學院,412007)

一、前言

在數學解題的過程中,我們常常會通過某種中介工具去構建該題與一種已知的、熟悉的數學模型之間的聯系,使之能夠通過這個模型來解答問題．為了解決一個難題,經常會先證明幾個重要的結論作為“引理”,這種“引理”其實也是模型,它往往是問題解決中的思考方向和關鍵工具[1].建立模型的主要目的就是為了解決問題,而建立模型可以縮短問題的推理過程,甚至能引導學生更直接地發現問題的本質[1].教師要在主要知識點通過多種方式來培養學生的模型思想.

二、 數學模型思想相關概述

數學模型是數學知識與方法的范式總結，是為了方便解決問題而提煉出來的.通俗地說,數學模型可以是形狀、公式、定理、概念、法則等．在義務教育階段,用字母、數字及其他數學符號所建立起來的不等式、代數式、方程等都是數學模型．數學模型思想本質上是培養學生靈活運用數學知識解決實際中的問題的能力,是一種數學的基本思想．

數學教學應結合具體教學內容,采用‘問題情境-建立模型-解釋、應用與拓展’的模式展開,讓學生經歷知識的形成與應用過程…[2].模型思想可以讓學生在學習的過程中形成解決問題的一種思維方式,也可以啟發學生的解題方向,不致于讓他們在碰到新穎題目時無從下手．數學模型最終能使學生理解概念的本質.教師要讓學生逐步地從學習模型思想,到自己歸納、總結模型,最后使自己體會建立模型的樂趣,從而提高他們學習數學的興趣和應用意識．

三、數學模型思想在初中數學解題中的應用

下面我們例談數學模型思想解決常見實際問題．

1.構建函數模型

函數是整個初中的重點內容,指因變量隨著自變量的變化而變化,它反映了現實世界眾多的關系和規律．例如計劃決策,方案投資、居民用度等,都可建立函數模型加以解決．其基本步驟是發現函數模型→建立函數模型→求解函數模型→確定實際問題的解．

例1某市為了鼓勵居民節約用水,采用分段計費的方法按月計算每戶家庭的水費,月用水量不超過20立方米時,按2元/立方米計費;月用水量超過20立方米時,其中的20立方米仍按2元/立方米計費,超過部分按2.6元/立方米計費．小明家小明家第二季度用水情況如下表:

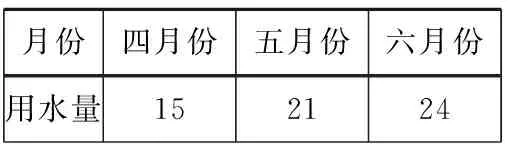
月份四月份五月份六月份用水量152124

小明家這個季度共交水費多少元?

解① 分析問題:根據題意,采用分段計費,應該分別建立模型.由于不同的用水量收費標準不同,所以可建立分段函數模型．假設每戶家庭月用水量為x立方米,當用水量不超過20立方米時,應交水費f(x)(元);超過20立方米時,應交水費g(x)(元),當季度總水費為W(元)建立如下函數模型．

W=四月份水費+五月份水費+六月份水費

其中f(x)=2x,(0≤x≤20)；

g(x)=2×20+2.6(x-20)，(x>20).

② 對于上述模型,形式比較復雜,可以適當進行化簡,便于后期的計算．通過化簡得到

其中f(x)=2x,(0≤x≤20)；

g(x)=2.6x-12，(x>20).

這就是最終的函數模型,當季總的水費W是由這兩個函數模型計算得出．

③ 求這個季度的應交水費W,只需將相應的用水量帶入模型,根據公式相加即可．

小結對于一些分段、分類型、分水平的問題,常常采用分段函數的模型來解決.值得注意的是分段函數模型每一段的定義域要符合題目所給的條件,也要準確地依據題意建立模型．

2.構建方程、不等式(組)模型

方程、不等式(組)是將現實中的問題數學化后,利用設未知數,代入等量或者大小關系式,再利用解方程(組)、不等式(組)的形式得到數學問題的解決,從而解決現實問題.現實生活中廣泛存在著數量之間的等量或不等量關系,如增長率、銷售定價、工程問題等問題,模型思想的關鍵是找出等量或不等量關系,設定合適的未知數,用未知數表示出來,就得到了我們的方程或不等式模型,從而得到問題的解決．

例2某文教店用1200元購進了A，B兩種羽毛球拍．已知A種羽毛球拍進價為每副12元,B種羽毛球拍進價為每副10元．文教店在銷售時A種羽毛球拍售價為每副15元,B種羽毛球拍售價為每副12元,全部售完后共獲利270元．

(1)求這個文教店購進A，B兩種羽毛球拍各多少副;

(2)若該文教店以原進價再次購進A，B兩種羽毛球拍,且購進A種羽毛球拍的數量不變,而購進B種羽毛球拍的數量是第一次的2倍,B種羽毛球拍按原售價銷售,而A種羽毛球拍降價銷售．當兩種羽毛球拍銷售完畢時要使再次購進的羽毛球拍獲利不少于340元,A種羽毛球拍最低售價每副應為多少元?

解① 分析問題:題目中出現了許多名詞,如進價、售價、獲利,我們需要找到它們之間的等量關系,以此來建立方程(組)模型．題中的獲利即利潤,利潤=售價-進價,根據題意,我們可得到兩個等量關系組:

又A種羽毛球拍的獲利=A種羽毛球拍的數量×每副B種羽毛球拍的獲利.

同理可得：

B種羽毛球拍的獲利=B種羽毛球拍的數量×每副B種羽毛球拍的獲利．

② 對于上述等量關系,我們不妨設文教店購進A種羽毛球拍x副,B種羽毛球拍y副,得到：

上述模型就是我們依據題目的等量關系建立的方程模型,要求文教店購進A，B兩種羽毛球拍各多少副,解出上述模型的未知數即可．

3.構建幾何模型

幾何模型是中考的重要知識點,對學生的空間想象能力要求比較高,還需要學生對各類模型有一定的熟悉度才能靈活運用．生活中隨處可見幾何,如航海、測量、道路橋梁設計等.隨著知識量的增加,幾何模型的應用范圍更廣、難度也更大．

例3如圖1,在等邊?ABC中,AB=6，N為線段AB上的任意一點,∠BAC的平分線交BC于點D,M是AD的動點,連結MB，MN.求MB+MN的最小值．

解① 分析:題中涉及到“動點”“最小值”等字眼,啟示學生去思考能不能轉化為“兩點之間線段最短”或者“垂線段最短”來解決問題.這里就涉及到了“將軍飲馬”模型,將同側的定點轉化為異側,利用以上兩個定理來解決問題．

② 找B點關于定直線AD的對稱點,即點C,當C，M，N三點共線,且CN⊥AB,MB+MN有最小值,過點C作CE⊥AB,垂足為點E,則最小值為CE的長．

以上模型屬于將軍飲馬問題中的“兩定一動”型,還有“兩動一定”“三動型”等等,其本質都是通過“兩點之間線段最短”以及“垂線段最短”來解決問題．類似于上述的幾何模型還有很多,比如“一線三等角”“費馬點定理”等等,許多題目都不是直接將模型呈現出來,而是需要學生以熟悉的幾何模型作為切入點,再要克服思維定勢,才能最終找到適合的解題方法．

4.構建概率模型

隨機事件發生的可能性大小的數值叫做概率.函數是研究變量之間確定的關系,而概率是研究變量之間不確定的關系．概率模型是最貼近生活的模型,因為隨機事件發生的可能性幾乎充盈在生活的每一個角落.如，“拋一枚硬幣,正面朝上的可能性有多大”“擲一枚骰子,骰到六點的可能性有多大”等.構建概率模型,能使上述問題更加直觀,且具有說服力．

例4甲、乙兩名同學玩一個游戲:在一個不透明的口袋中裝有標號分別為1,2,3,4的四個小球(處標號外無其他差異).從口袋中隨機摸出一個小球,記下標號后放回口袋中,充分搖勻后,再從口袋中隨機摸出一個小球,記下該小球的標號,兩次記下的標號分別用x,y表示，若x+y為奇數，則甲獲勝；若x+y為偶數，則乙獲勝你認為這個游戲對雙方公平么?

解① 分析問題:將此問題抽象為數學問題即為x+y為奇數和偶數的概率分別是多少?哪個概率大?

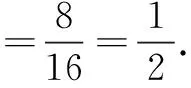
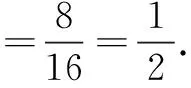
∴P(甲獲勝)=P(乙獲勝)

既然獲勝的概率是一樣的,所以這個游戲對雙方公平．

在初中階段的概率模型中,古典概型是最常見的.準確地應用具體的概率模型是描述事件可能性的中心環節．

四、結束語

通過以上例題的分析,我們發現數學模型思想在解題中的有效應用,不僅可以降低解題的難度、提高了解題效率,也能更好地讓學生理解解題過程的合理性.這對學生數學素養的的培育有著積極作用.教師的關注點應該放在如何引導學生發現問題中的模型和建立模型上.讓學生經歷感知模型、建立模型、拓展模型歸納模型、遷移模型這一過程,不僅可以提高學生思維的質量,還可以全面提升學生的數學核心素養．