探索幾何“不變性” 感悟數學“理性美”
——《新課標》理念下圖形翻折問題深入研究
楊金增 黃祥勇
(四川省成都市金牛區教育科學研究院,610000) (四川省成都市教育科學研究院,610000)
本文以一道中考試題開展動態幾何教學探究,設法運用“度量”來觀察不變的幾何規律,在求“變”中尋找“不變”,培養學生以“不變”應“萬變”的思維能力,發揮數學滲透“理性美”的育人功能.
一、 原題呈現
(2021年成都中考第24題)如圖1,在矩形ABCD中,AB=4,AD=8,點E,F分別在AD、BC上,且AE=3,按以下步驟操作:
第一步,沿直線EF翻折,點A的對應點A′恰好落在對角線AC上,點B的對應點為B′,則線段BF的長為______;
第二步,分別在EF,A′B′上取點M,N,沿直線MN繼續翻折,使點F與點E重合,則線段MN的長為______.
二、 核心素養視角下試題的特色解讀
1.起點低,入手易
本題“矩形的長是寬的2倍”,背景數量關系簡單.第(1)問,“沿EF折疊,A的對應點A′恰好落在對角線AC上”,依據“線段AA′被EF垂直平分”,過點F作FP⊥AD于P,利用∠PFE=∠DAC(或者?PFE∽?DAC),求出PE,進而可求BF.該題設為兩小題填空,共4分.對于數學中等生,第1問的2分是可以得到的,入手還是比較容易.
2.立意高,內涵豐
從兩個問題的結構上看,設問以“第一步”、“第二步”的方式,意在提醒翻折操作是“順次的”,都是研究“翻折”前后“相關線段的位置關系”與“相關線段數量關系”及“對應”的規律.該題妙在第二次翻折操作,打破了“一次翻折”的常規.著力考查學生能否抓住“軸對稱”的性質,發現翻折變化過程中“變與不變”的規律,能否“化動為靜”,能否建立“相似、全等”數學模型求解“折痕”所在線段MN的長度.
三、 解法賞析
1.求線段BF的長
解法1如圖2,過點F作FP⊥AD于點P,設EF交AA′于點Q,
∵EF⊥AA′于Q,∴∠DAC=∠PFE.
∴AP=AE-PE=3-2=1,
∴BF=AP=1.
解法2如圖3,延長AB,EF交于點T,設EF交AA′于點Q.
∵EF⊥AQ,∴∠T=∠EAQ,
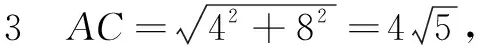
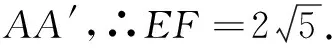
2.求線段MN的長
解法1如圖4,延長NM交AB于P.
由“翻折”對稱性知,MN=PM,連結PE,PF,由對稱性知PE=PF,
設AP=x,則x2+32=(4-x)2+12,
解得x=1,
∴AP=BF,∴?PAE≌?FBP,
∴∠APE=∠PFB,∴∠APE+∠BPF=90°,∴∠EPF=90°.
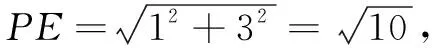
解法2如圖5,延長AB、EF交于T.
由軸對稱知,延長A′B′也交于點T,由題意易知MN垂直平分線段EF,
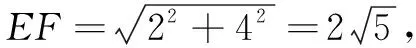
解法3如圖6,連結EN,FN,由翻折的對稱性知EN=FN.
設A′N=x,則B′N=4-x,由(EA′)2+(NA′)2=(FB′)2+(NB′)2得32+x2=12+(4-x)2,解得x=1,
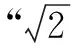
四、教學啟示
1.解后追問 重在發現
幾何解題教學中,研究圖形變化、探索變化規律,既要注重“一題多解”思維發散訓練,又要注重“多題一解”通性通法的思維聚合訓練.在問題解決之后,多一點“追問與變式”,追問:條件不變的情形下,還可以提出哪些新問題?改變部分條件,又能提出哪些新問題?將題設中的數據改變成字母,將問題拓展推廣,能否推導出一般性的結論?
第一步翻折,圖形位置關系是確定的,所以相關線段的數量也是確定的,所以圖中線段長度都是可以求解的.解后追問:
① 求線段EF,A′C,AA′,A′D的長;
② 條件改為:若點A的對應點A′恰好落在對角線BD上,點B的對應點為B′,求線段BF的長;
③ 條件改為:點A的對應點A′恰好落在對角線上(注意沒有具體說在哪條對角線了),點B的對應點為B′,求線段BF的長.
第二步翻折,解后追問:
① 翻折后,設B′落在B″處,證明:B″在AD上;
② 求線段A′B″,DB″,CB″的長.
2.數字變字母,特殊到一般
拓展變式,探究一般矩形、一般平行四邊形的相關結論.
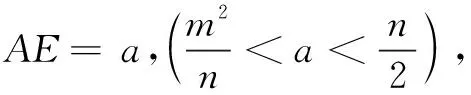
第一步,沿直線EF翻折,點A的對應點A′恰好落在對角線AC上,點B的對應點為B′,則線段BF的長為______(用m,n,a表示);
第二步,分別在EF,A′B′上取點M,N,沿直線MN繼續翻折,使點F與點E重合,則線段MN的長為______(用m,n,a表示).
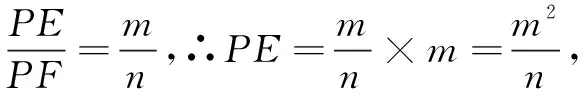
QB=m-x,
由AE2+AQ2=QB2+BF2得,
∴QE2=a2+x2
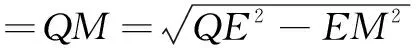
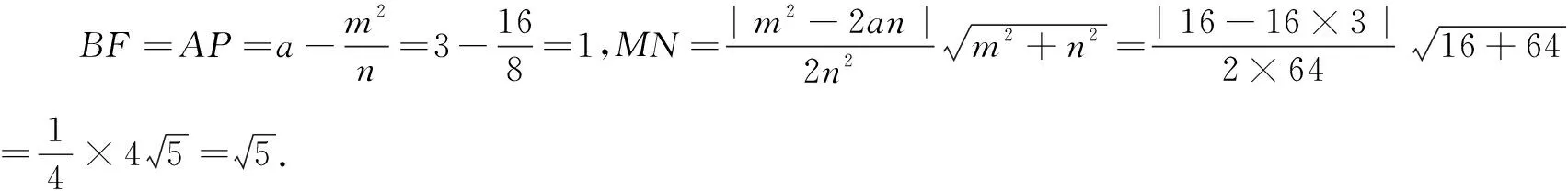

B′,則線段BF的長為______(用m,n,a表示);
解過點C作CG⊥AD于點G,則
AG=n-mcosθ,
設EF交AC于點H,則
∴BF=BC-FC

再繼續翻折,使點F與點E重合的問題,留給讀者去思考和研究.
3.改造原題,感悟立意
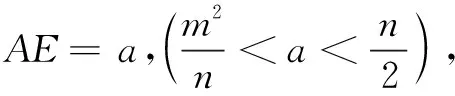
這樣改造原題,提高了問題的難度,它有兩個難點:一是字母運算,具有抽象性;二是A′落在矩形的對角線上,需要分兩種情況討論,否則容易漏解.

