基于問題驅動的“以學生為中心”的矩陣乘法教學設計研究

李艷艷，蔣建新，高美平，黃衛華

（文山學院人工智能學院，云南 文山 663099）

《線性代數》課程是理、工、農、經管類專業必修的基礎數學課之一，關于線性代數的課程建設、教學改革，以及教學設計等，已經進行了各具特色的研究。

本文把研究視角放在具體的一節課的教學設計研究上，從小視角見大問題。矩陣乘法選自線性代數第二章第2節矩陣的運算部分，矩陣是線性代數問題的主要工具，矩陣乘法是矩陣的重要運算，不管是對于后續知識的學習，還是實際的應用，都發揮著承前啟后和不可替代的作用。本文著重從理論角度、實踐應用角度、課程思政角度、學生中心角度研究矩陣乘法的教學設計問題。

1 預備階段

1.1 教材分析

矩陣與矩陣的相乘運算是矩陣中常用的運算，是學習矩陣的逆、矩陣的對角化等本課程后續內容的基礎，通過本節的學習，要求復述矩陣的乘法運算規則，應用矩陣的乘法運算滿足的規律解決問題。特別地，要識記矩陣乘法運算不滿足的規律，認識左乘和右乘的概念。

1.2 學情分析

學生已經掌握了矩陣的概念，掌握了矩陣的加法運算和數乘運算，矩陣的加法是兩個矩陣相加，要求相加的兩個矩陣是同型矩陣。那么兩個同型的矩陣是否也可以相乘呢？運算規則是什么？帶著這些問題，學習矩陣的乘法運算。

1.3 教學目標

（1）復述兩個矩陣相乘C=AB的運算中，必須滿足前一個矩陣的列數等于后一個矩陣的行數才可以相乘，掌握乘法運算法則。

（2）識記矩陣乘法運算不滿足的規律，深入理解矩陣的概念。

（3）靈活、熟練利用矩陣乘法解決矩陣運算的問題。

1.4 教學重點

（1）兩個矩陣相乘C=AB的運算法則中，前提條件、結果類型、乘積之后元素的特點。

（2）矩陣乘法運算與實數域中兩個實數乘法的差別，矩陣乘法運算不滿足交換律和消去律。

1.5 教學難點

（1）矩陣乘法的運算規則。

（2）矩陣乘法不滿足的規律。

2 從理論角度的教學設計

目前文山學院使用的線性代數教材是同濟大學工程數學——線性代數，貫穿教材的主線是求解線性方程組，重要載體是矩陣，那么矩陣運算的學習就顯得尤為重要。矩陣乘法不像實數乘法那樣直接，但又關聯度緊密。為了使該問題的認識能更加自然和深刻，所以采用了從具體到抽象，從特殊到一般的設計思路，以及類比的數學思想方法。

2.1 從具體到抽象

通過工廠總收入和總利潤問題的簡便解決，探究矩陣乘法法則，然后將該法則從具體抽象到一般情況。

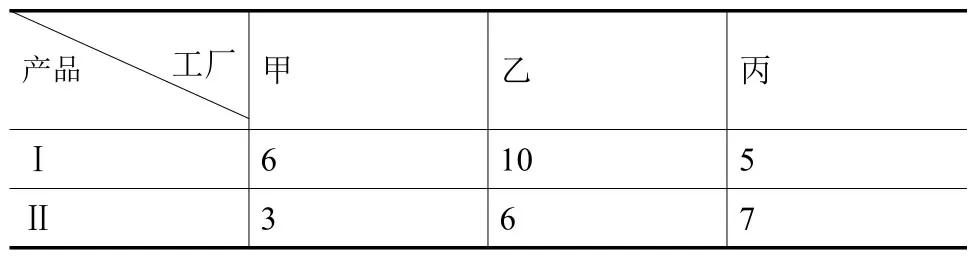
表1 2017年各工廠的各產品產量（噸）

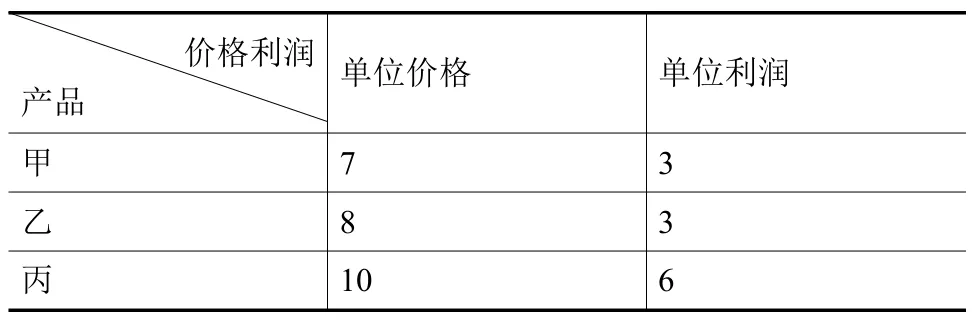
表2 各產品的單位價格及單位利潤（萬元/噸）

表3 各工廠一年的總收入及總利潤（萬元/噸）

將上述3個表格分別抽象成矩陣

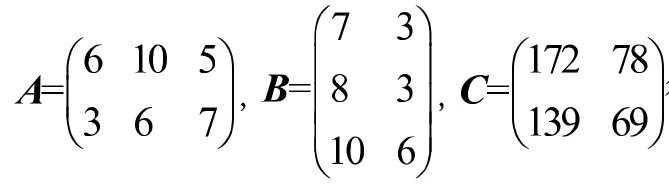
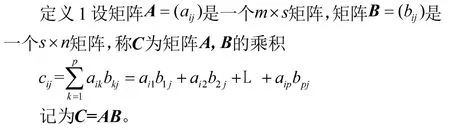
2.2 從特殊到一般

矩陣乘法的性質，與傳統認知中的實數乘法有著一定的差異和相似，所以在第一階段基礎初級的訓練中，設計兩個例題，分別是針對矩陣乘法不滿足交換律和消去律的探討，從而將其不滿足的性質從特殊推廣到一般。

兩個例題讓學生分組完成，在表象結果的基礎上，引導學生思考矩陣乘法不滿足的性質，并深刻的分析其原因，使學生的認知發生質的飛躍。

2.3 類比的思想

矩陣乘法的性質，通過類比實數乘法的性質，平行得出結果，充分體現了舊知類比得出新知的理念。具體有

3 從實踐的角度設計應用

線性代數來源于生活實際，又很好地服務于科學研究和生活，所以在導入環節（情境創設）通過大量的圖片介紹其廣泛的應用。在升華環節，通過具體的實例分析其詳細的應用。通過表象感觸和深入探討的結合，使學生深刻領悟到矩陣乘法的廣泛應用。

（1）導入環節：首先從矩陣乘法在圖片加密，字體變換，人臉識別，搜索引擎，圖像處理，我國自主研發的飛機設計中的應用案例，進行課題導入。緊接著通過如何快速計算工廠的總收入和總利潤問題，歸納、總結、抽象矩陣乘法的法則。

（2）應用環節：通過設計，明文—加密—密文，展示了矩陣乘法的應用，同時也為，密文—解密—明文，中逆矩陣的學習埋下伏筆。

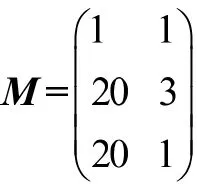
4 從課程思政的角度設計

課程思政貫穿于本節課的始終，從多角度和多維度進行融入，有愛國情懷，數學史、數學文化以及數學家的精神，攻堅克難的勇氣，團隊協作精神和精益求精精神等。

4.1 愛國情懷

情境創設、課題引入環節，設計了運20和殲20的總設計師——西北工業大學最牛上下鋪——楊偉與唐長紅，感悟他們為了國之重器奉獻終生的精神。

4.2 數學史、數學文化以及數學家的精神方面

一是科學家的執著精神。介紹了英國數學家凱萊的成長成才經歷，在被迫放棄自己熱愛的工作時，也沒有間斷自己為之著迷的數學研究。

二是團隊合作的力量。凱萊與他的金牌搭檔英國數學家西爾維斯特，一起為了代數型不變理論的研究的奮斗歷程。

三是奉獻精神。積極主動投身社會工作，為了劍橋大學接收女性學生發揮了很大的作用，借此引出“七一勛章”獲得者，“全國優秀共產黨員”張桂梅老師。

4.3 攻堅克難的勇氣

設計了三個逐步遞進的環節，梯度式的上升，在實踐中錘煉學生求真的意志和能力，攻堅克難的勇氣。

第一階段：基礎初級階段—簡單的矩陣乘法法則的練習；

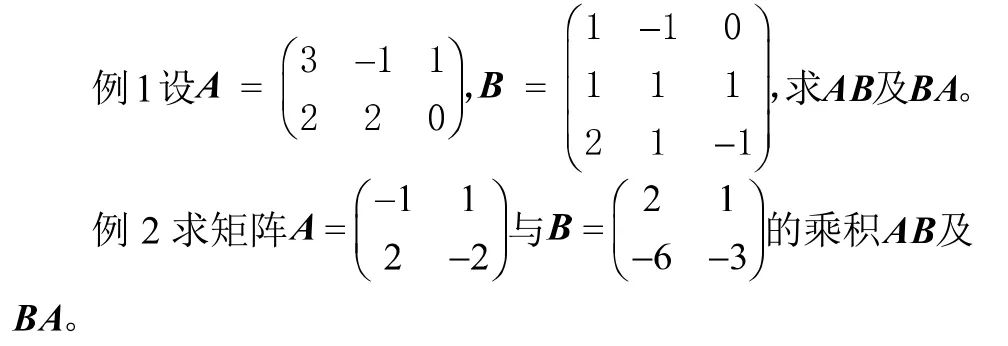
第二階段：提高、應用—重走長征路，體會凱萊發明矩陣乘法的初衷，深刻感受科學家的求真精神，以及矩陣乘法的廣泛應用。

例3已知兩個線性變換

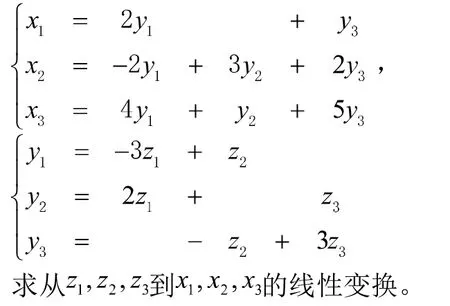
第三階段：延伸、拓展—巧妙利用矩陣乘法的結合律，解決矩陣冪的計算問題。

4.4 通過合作式學習，培養學生的團隊協作精神和精益求精精神

團隊協作精神和精益求精精神貫穿整個教學設計的始終。小組合作探究環節，兩人一組，在團隊成員之間可以對探究結果反復補充，直到滿意為止。

5 學生中心

“以學生為中心”的理念，是整個教學設計的出發點、落腳點、產出點，也是靈魂之所在。

（1）兩次學習通3分鐘測試（課前、課后）。

（2）學生小組合作（兩兩一組），希沃白板學生作品展示，讓學生時時處處、真真切切參與課堂。在充分體現“學生中心”的基礎上，教師隨時隨刻掌握學生的學習情況。

（3）通過PPT、希沃白板、黑板、學習通的無縫切換，讓智慧課堂淋漓盡致的展現，從而顯著提高學生課堂參與度和課堂的時效性。

6 總結

本文研究了工程數學——線性代數的教學設計問題，基于教材、學情、教學目標、教學重難點，從理論、實踐、課程思政、學生中心四個角度，通過問題驅動和案例式的方法，秉承學生中心的理念，進行了教學設計的深層次探討和實踐。