運用復數(shù)思維解決非復數(shù)類問題“五法”
?福建省廈門市第六中學 吳 瑾
1 引言
高中關于復數(shù)的系統(tǒng)學習,主要集中在人教版選修2-2第三章“數(shù)系的擴充與復數(shù)的引入”.復數(shù)思維是建立在復數(shù)知識之上的一種重要數(shù)學思維,它利用復數(shù)的代數(shù)式、三角式,模及其運算的幾何意義,為我們解決代數(shù)、三角、幾何等學科中的非復數(shù)問題提供了又一個思維方法和解題途徑.
2 解決非復數(shù)問題“五法”
2.1 利用復數(shù)冪的周期性
根據(jù)代數(shù)式的對稱性和排列組合數(shù)的規(guī)律性,我們可以將其轉化為復數(shù)問題[1],利用復數(shù)的性質(zhì)進行求值或證明,從而達到快速解題的目的.
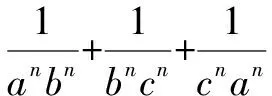
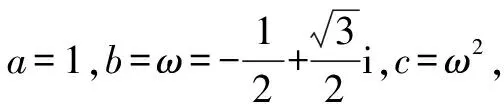
=1+ωn+(ω2)n
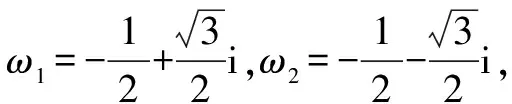
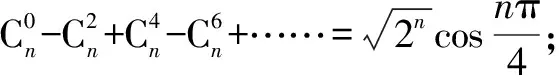
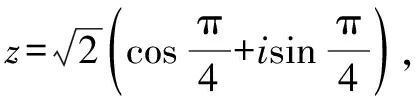
又根據(jù)二項式定理,得
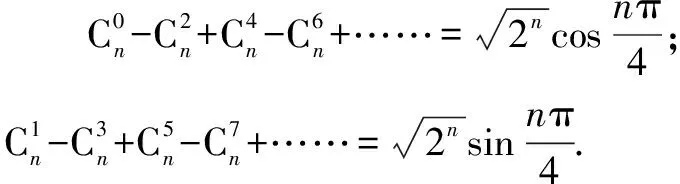
方法與技巧:通過觀察,發(fā)現(xiàn)題目中這些組合數(shù)的上標從0,1,2,3起,組合數(shù)的符號具有“+、+、-、-”的周期性,自然會聯(lián)想到復數(shù),進而利用復數(shù)的性質(zhì)完成證明.本題主要運用了in的周期性及棣莫佛定理.
2.2 利用復數(shù)的模
利用復數(shù)模的不等式,能夠為我們解決實數(shù)的有關問題提供模型,把諸如求函數(shù)值域、解(證明)不等式、求極值等問題轉化為復數(shù)問題.這種間接的解題方法具有“化繁為簡”的優(yōu)越性.
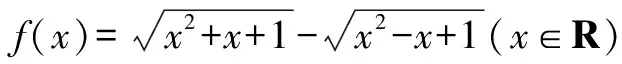
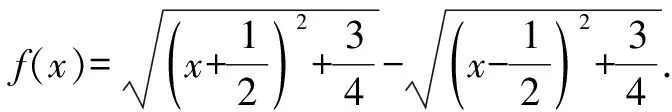
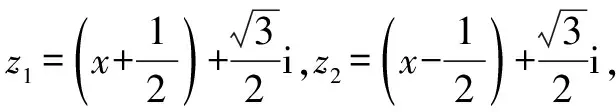
f(x)=|z1|-|z2|.
因為 ||z1|-|z2||≤|z1-z2|=1,
①
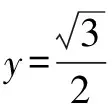
所以||z1|-|z2||<1.
故所求函數(shù)的值域為(-1,1).
方法與技巧:本題巧妙地利用了復數(shù)模的不等式,將函數(shù)問題轉化為復數(shù)問題.從本題的求解過程可以發(fā)現(xiàn)以下規(guī)律,對于復數(shù)模的不等式||z1|-|z2||≤|z1±z2|≤|z1|+|z2|,當且僅當z1=kz2(k>0)時,|z1+z2|=|z1|+|z2|,|z1-z2|=|z1|-|z2|;當且僅當z1=kz2(k<0)時,|z1+z2|=||z1|-|z2||,|z1-z2|=|z1|+|z2|.
例4已知|a2-b2|+2|ab|=1(a,b∈R).
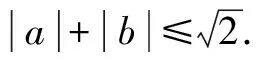
證明:設z=a+bi,則z2=a2-b2+2abi.于是 |Re(z2)|+|Im(z2)|=1.
因為對于任意復數(shù)z,總有
②
所以可得|z|2=|z2|≤|Re(z2)|+|Im(z2)|=1,即|z|≤1.
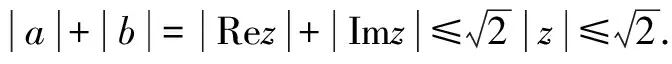
方法與技巧:本題是運用復數(shù)的模證明不等式的典型實例,其中②式揭示了復數(shù)的模與其實部、虛部絕對值之間的關系,把a2-b2與2ab看作復數(shù)(a+bi)2的實部與虛部也是解題常用的一種技巧.
2.3 利用復數(shù)積(商)的輻角
在求三角函數(shù)值的一些問題中,可以利用復數(shù)積的輻角等于兩個復數(shù)的輻角之和,或者運用共軛復數(shù)的性質(zhì)進行等價變形等方法來求解,這樣既可以避免繁瑣的計算,又容易找到解決問題的突破口.
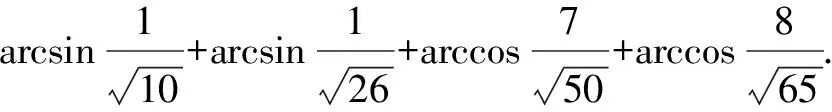

所以原式=arg(3+i)+arg(5+i)+arg(7+i)+arg(8+i)
=2kπ+arg[(3+i)(5+i)(7+i)(8+i)]
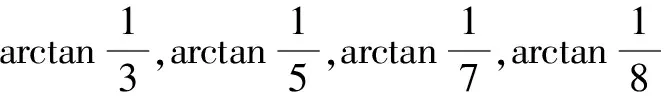

方法與技巧:本題將反三角函數(shù)中的角轉化為復數(shù)的輻角,進而利用復數(shù)積的輻角等于各復數(shù)輻角之和,充分體現(xiàn)了用復數(shù)思維解這類題的優(yōu)越性.
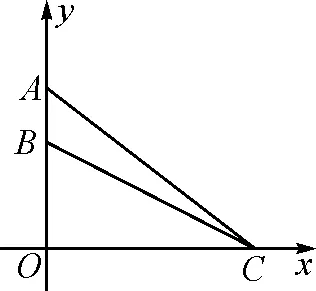
圖1
例6如圖1,在平面直角坐標系中,在y軸的正半軸(坐標原點除外)上給定兩點A,B,試在x軸的正半軸(坐標原點除外)上求點C,使得∠ACB取得最大值.
解:以直角坐標系確定一個復平面,設A,B,C三點對應的復數(shù)為zA,zB,zC,則
zA=ai,zB=bi(0
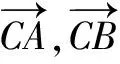
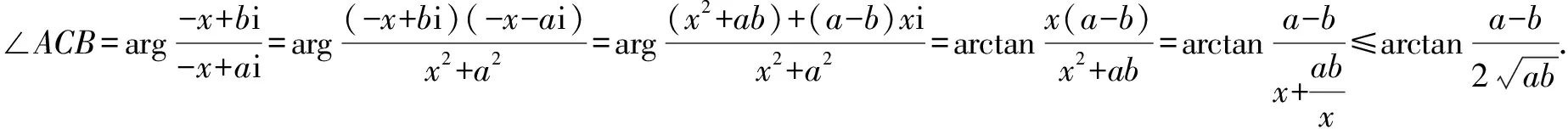
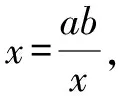
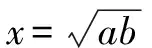
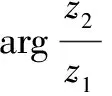
2.4 利用復數(shù)的n次方根
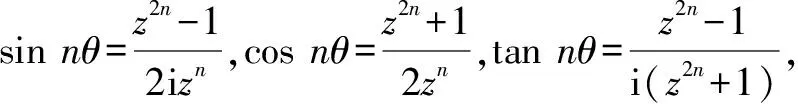
例7求tan 9°+cot 117°-tan 243°-cot 351°的值.
解:設z=cos 9°+isin 9°,則z10=i.
所以 tan9°-cot351°+cot117°-tan243°
=tan9°+cot9°-tan27°-cot27°
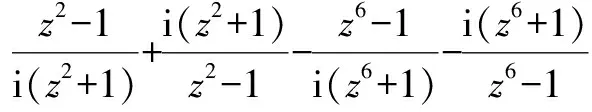
方法與技巧:本題先利用誘導公式,將諸角化為某一個角的倍數(shù)關系,以便應用棣莫佛定理的變形公式.由解題的過程可以看出,運用復數(shù)思維來步步化簡的方法顯得非常簡潔明快.
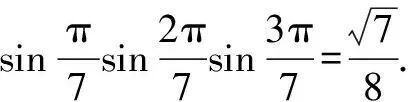
證明:因為z7-1=(z-1)(z6+z5+z4+z3+z2+z+1),又根據(jù)根的定義,有
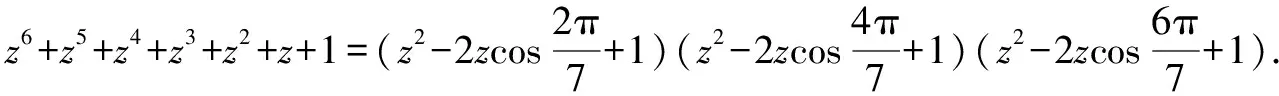
令z=1,得
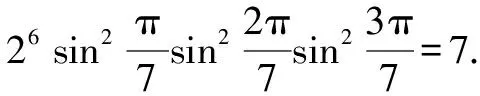
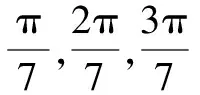
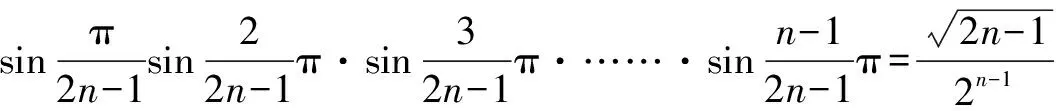
2.5 利用向量的旋轉與共線
對于解析幾何中涉及到的較復雜的特殊角的多邊形類問題,如果利用復向量的旋轉與共線的性質(zhì)來解決會顯得很簡捷.
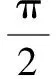
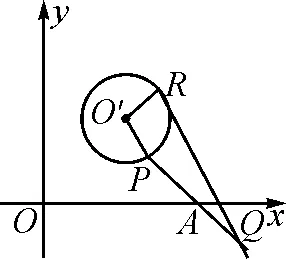
圖2
解:如圖2,根據(jù)直角坐標系確定一個復平面,設點P,Q,A對應的復數(shù)分別為zP,zQ,zA,根據(jù)點P,Q關于點A對稱可知z→AP=z→QA.
即
zP-zA=zA-zQ.
③
又因為zA=9,所以zQ=18-zP.
因為z→O′P=zP-zO′=zP-(5+5i),所以z→O′R=z→O′P·i=zPi+(5-5i).
于是zR=z→O′R+zO′=zPi+(5-5i)+(5+5i)=zP·i+10.
z→QR=zR-zQ=(zP·i+10)-(18-zP)=(1+i)·zP-8=[zP-(5+5i)](1+i)+5(1+i)2-8=[zP-(5+5i)](1+i)-(8-10i).
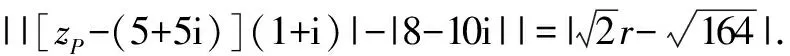
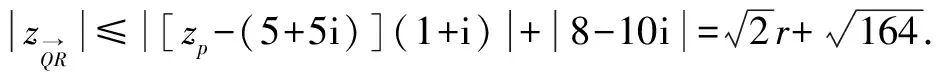
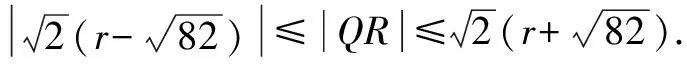
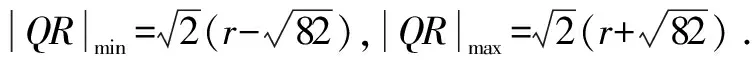
方法與技巧:本題中運用共線向量導出③式以便應用zA=9;將zP配湊成zP-(5+5i)以便取模得到半徑,這些都是我們應當學習和掌握的解題技巧.
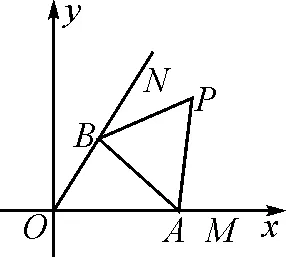
圖3
例10如圖3,∠MON=60°,邊長為a的正三角形ABP在∠MON內(nèi)滑動(不能翻轉),使點A始終在OM上,點B始終在ON上,求點P的軌跡方程.
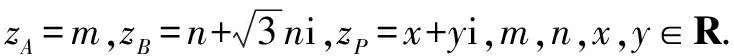

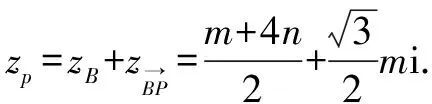

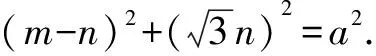
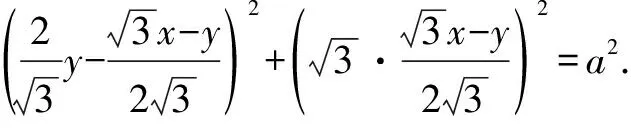
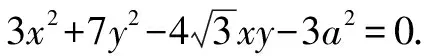
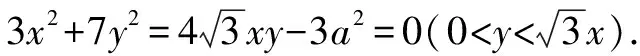
方法與技巧:本題是把求動點軌跡的問題轉化為復數(shù)(復平面)問題來求解,除了運用復數(shù)思維,本題還體現(xiàn)了求軌跡問題的設參、消參等參數(shù)思想.
3 總結
從上述典型例題的解答中可以看到,運用復數(shù)思維解決非復數(shù)類問題的方法和技巧具有廣泛性、實用性和極大的靈活性.我們應該通過多種練習,學習、領會和掌握這些方法與技巧,這有助于開闊我們的思路,不斷提高綜合解題能力.

