巧借氣體虛擬態化解變質量難題

郭公禮

(新疆維吾爾自治區烏魯木齊市第一中學 830000)

理想氣體的變質量問題，可根據不同情況分別使用克拉伯龍方程、理想氣體狀態方程、氣體實驗定律以及密度公式，分態方程等等進行求解，由于處理方法多種多樣，處理技巧各不相同，應用公式多且靈活多變，對于大多數學生來說掌握起來還有一定難度，能不能找到一種通用方法，讓學生易學、易懂、易掌握呢？下面分類介紹巧借虛擬狀態，求解氣體變質量問題的通用方法.

1 漏氣問題

例1有一容積是10L，內裝有1.80kg的醫用氧氣瓶.使用前，瓶內氧氣壓強為140atm，溫度為37℃.當給患者輸氧以后，發現這個氧氣瓶瓶內氧氣壓強只剩了50atm，此時溫度也降為27℃，試求這位患者消耗的氧氣的質量.

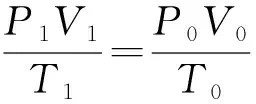
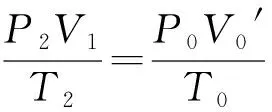
點評解決變質量問題的關鍵就是把兩種不同狀態的氣體都轉化為同一溫度，同一壓強的氣體虛擬態，而且虛擬態的壓強與溫度可以隨意選取，這樣只要算出兩種虛擬態的體積比，就很容易求出質量比.比起使用密度公式，這是學生最容易聽懂且最容易掌握的方法，可以幫助學生理解問題的本質，雖然不是最簡便的運算步驟，但是思路簡單清晰，能達到一教就會，一練就對的目的，真正做到以不變應萬變.

2 分裝問題

例2 新型冠狀病毒肺炎是一類傳染性極強的急性傳染病.當前，新型冠狀病毒奧密克戎新變異株傳染性更強，防控形勢仍然嚴峻.該病主要發病位置在肺部，表現為呼吸困難等，因此治療過程中有些患者急需進行吸氧.已知某鋼瓶容積180L，在室外測得其瓶內氧氣壓強為4×106pa，環境溫度為-23℃，現在先將其移至室內靜置(鋼瓶的熱脹冷縮可以忽略不計)，待溫度與室內相同時，將其對容積5L內部氣壓為2×105pa的小鋼瓶分裝，分裝后每個小鋼瓶壓強為2×106pa，已知醫院病房內溫度27℃且最多可分裝多少瓶小鋼瓶供病人使用？(假設分裝過程中大小鋼瓶溫度均保持不變).

答案：56.

點評解決此題的關鍵就是把被分裝的對象和分裝對象的不同狀態的氣體都轉化為同一溫度，同一壓強的氣體，雖然虛擬態壓強與溫度可以隨意選取，但為了簡化，一般選取題目中已有壓強與溫度；然后利用質量守恒即總體積守恒即可解決分裝問題.在不用克拉伯龍方程等超綱知識的前提下，構建統一的模式解法，學生更易于上手，只要稍加練習即能熟練.

3 充氣問題

例3 2021年11月，王亞平從天和核心艙節點艙成功出艙，成為中國首位出艙行走的女航天員，標志著中國女航天員首次實現“太空漫步”．同時，王亞平身著的新艙外航天服也在首次亮相．在核心艙內時，航天服內氣壓為1.0×105pa，所充氣體體積為2L，由于艙外氣壓低，航天服內氣體體積會膨脹，變為4L，設航天服內氣體的溫度不變，將航天服視為封閉系統，其內部氣體視為理想氣體．若開啟航天服的充氣閥門，向航天服內充入同種氣體，保持航天服內氣體體積為4L，使航天服內的氣壓緩慢恢復到0.9×105pa，則需補充壓強為1.0×105pa的等溫氣體多少升？

解析由于溫度相同，只要轉化為壓強相等，利用總體積守恒的原理即可解決，設虛擬末態壓強P0為1.0×105pa，把末態(P1、V1)(即航天服4L氣壓緩慢恢復到0.9×105pa)，轉化為虛擬態的體積V0，由等溫公式：P1V1=P0V0得V0=3.6L,顯然需要補充ΔV=1.6L.

點評分裝問題與充氣問題互為相反的過程，本質上屬于同一問題.在溫度相同的條件下，利用等溫的規律求出虛擬態的體積，再利用質量守恒即體積守恒即可順利解決此類問題.

4 抽氣問題

圖1

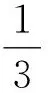
例5 如圖2所示，用一體積為ΔV的小型活塞式抽氣機對體積為V0的容器A中的氣體進行抽氣.已知容器A中初始的氣體壓強為p0，設抽氣過程中氣體溫度均保持不變．求抽氣機抽動n次后，容器A中剩余氣體的壓強pn.

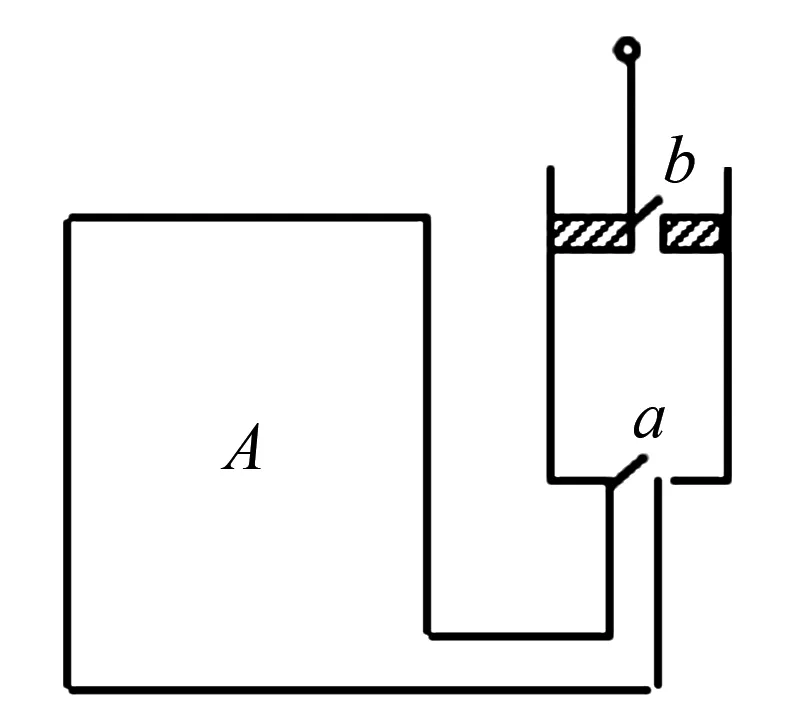
圖2

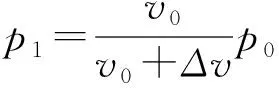
點評利用連續的虛擬態進行遞推是解決連續抽氣的有效方法.

5 混合問題

例6 如圖3所示，兩容積相同的啞鈴型容器A、B，用體積可以忽略的細長直導管相連，初始時A、B均封入壓強為p，溫度為T的相同理想氣體，現僅對左側氣體加熱，使A內溫度升溫至T′，右側容器B內氣體溫度始終為T.求穩定后A容器的氣體壓強.

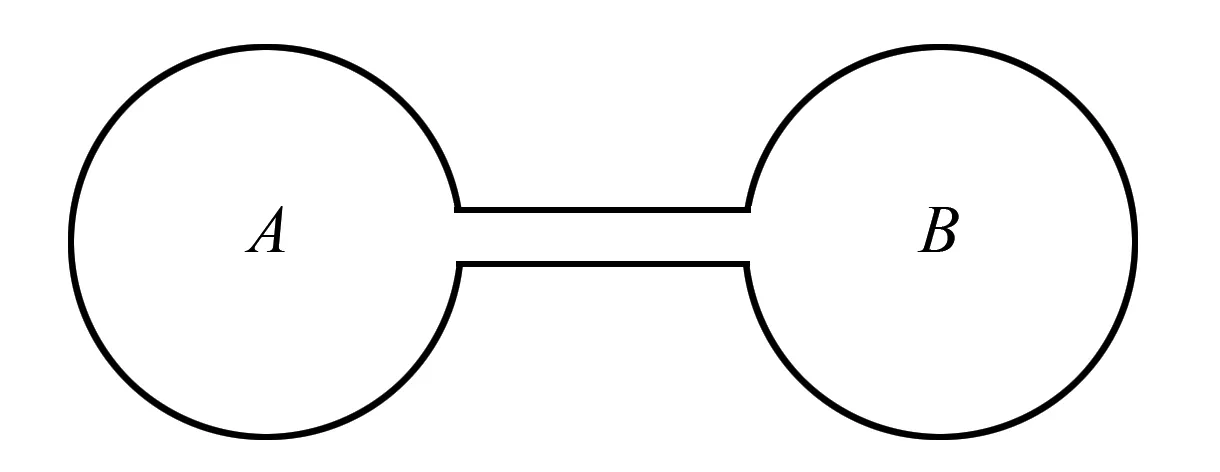
圖3

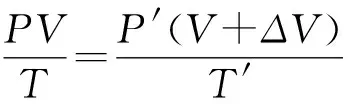
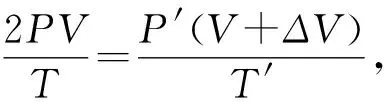
點評對于需要混合的氣體A、B先當成一個整體，運用氣體狀態方程統一轉化特定的虛擬狀態C，然后對虛擬狀態C進行“分裝”即可解決.方法一則是先把A轉化為特定的虛擬狀態D,把D分成終態A′、B′兩部分，把B′與B兩部分氣體利用“充氣”原理即可解決.方法二叫“先整體后隔離”，方法一叫“先隔離后整體”.

總之：所謂運用虛擬狀態解題，本質上是把克拉伯龍方程(PV=nRT)中的nR用統一的壓強、溫度和虛擬出一個新體積來表達，再利用質量守恒即虛擬的新體積守恒來解題,而所謂氣體變質量問題就變成了虛擬態體積的聚散問題.這有利于學生把握問題本質，找到統一解法，提升學生的學科素養.