基于素養導向和能力立意的高考數學備考策略
——2017-2021年全國卷中解析幾何解答題分類綜述

巨小鵬

(陜西省漢中市龍崗學校 723102)

平面解析幾何是選擇性必修主題二幾何與代數的內容，是創立微積分的基礎.其方法就是通過建系，借助直線、圓與圓錐曲線的幾何特征，導出相應方程，再用代數的方法研究其幾何性質，完美體現了數形結合思想.學生在學習過程中往往有這樣的幾個難點：一是對基本概念和基本公式理解不夠深刻；二是對解析幾何中所要用到的思想和方法掌握不夠；三是代數運算能力不夠.針對這些難點，依據新課程標準，理解基本概念，依托高考真題，總結規律，掌握方法，把握其內在邏輯，優化計算方法.

1 精準領會新課程標準要求

1.1 新舊課程標準教學要求區別

新課標刪除了“體會斜截式與一次函數的關系”，明確了“掌握平面上兩點的距離公式”，增加了能解決一些“實際問題”.對知識內容的整合，用代數法研究幾何問題，體現數形結合思想是本章內容的核心，這種思想貫穿該內容教學的始終.新課標對拋物線的要求是了解，難度也有所降低；舊課標“能用坐標法解決一些與圓錐曲線有關的簡單幾何問題(直線與圓錐曲線的位置關系)和實際問題”降為“了解橢圓和拋物線的簡單應用”，增加了“平面解析幾何的形成與發展”，引導學生感悟數學的文化價值.刪除了“曲線與方程”相關內容.

1.2 四了解、四探索和四能

了解：了解圓錐曲線的實際背景；了解拋物線與雙曲線的定義、幾何圖形和標準方程，以及它們的簡單幾何性質；了解拋物線與雙曲線的定義、幾何圖形和標準方程，以及它們的簡單幾何性質；了解橢圓、拋物線的簡單應用.

探索：探索確定直線位置的幾何要素；探索并掌握直線方程的幾種形式(點斜式，兩點式及一般式)；探索并掌握平面上兩點間的距離公式，點到直線的距離公式；探索并掌握圓的標準方程與一般方程.

能：能根據斜率判定兩條直線平行或垂直；用解方程組的方法求兩條直線的交點坐標；根據給定直線、圓的方程，判斷直線與圓，圓與圓的位置關系；能用直線和圓的方程解決一些簡單的數學問題與實際問題.

重點提升學生直觀想象、數學運算、數學建模、邏輯推理和數學抽象素養.

1.3 高考考情統計分析

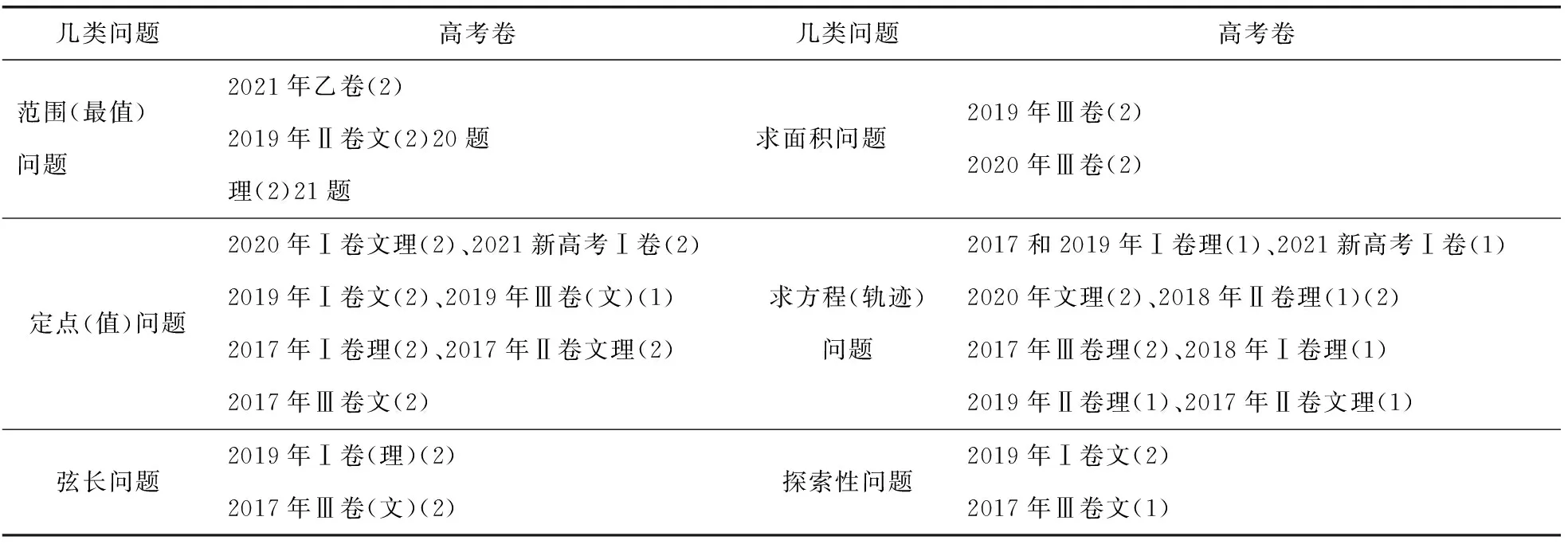
幾類問題高考卷幾類問題高考卷范圍(最值)問題2021年乙卷(2)2019年Ⅱ卷文(2)20題理(2)21題求面積問題2019年Ⅲ卷(2)2020年Ⅲ卷(2)定點(值)問題2020年Ⅰ卷文理(2)、2021新高考Ⅰ卷(2)2019年Ⅰ卷文(2)、2019年Ⅲ卷(文)(1)2017年Ⅰ卷理(2)、2017年Ⅱ卷文理(2)2017年Ⅲ卷文(2)求方程(軌跡)問題2017和2019年Ⅰ卷理(1)、2021新高考Ⅰ卷(1)2020年文理(2)、2018年Ⅱ卷理(1)(2)2017年Ⅲ卷理(2)、2018年Ⅰ卷理(1)2019年Ⅱ卷理(1)、2017年Ⅱ卷文理(1)弦長問題2019年Ⅰ卷(理)(2)2017年Ⅲ卷(文)(2)探索性問題2019年Ⅰ卷文(2)2017年Ⅲ卷文(1)

從統計明顯看出：(1)解答題第一問考查軌跡方程比較多，難度不大，考查基礎概念，基本方法；(2)定點(值)問題也是第二問常考類型，然后是范圍(最值)問題，其中可能與函數最值或者不等式交匯考查；(3)探索性問題也值得關注，試題本身的開放性只有在探索中才能體現出學生思維的方向性，作為選拔性考試，難度稍大.

2 幾個常見問題多視角通法分析

2.1 解決范圍(最值)問題中的多個視角

求范圍(最值)問題常常將目標轉化至函數或者不等關系，此時審視角度較多，比如利用幾何特征數形結合、判別式、求值域(二次函數和求導函數法較多)、基本不等式、正余弦定理、三角換元(參數方程法較多)、利用題中隱含條件建立不等關系或者利用線性規劃及其綜合方法解決問題.

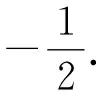
(1)求C的方程，并說明C是什么曲線；

(2)過坐標原點的直線交C于P，Q兩點，點P在第一象限，PE⊥x軸，垂足為點E，連接QE并延長交C于點G.

(ⅰ)證明：△PQG是直角三角形；

(ⅱ)求△PQG面積的最大值.

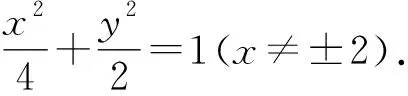
(2)(ⅰ)設直線PQ的方程為y=kx,可知k>0,直線PQ的方程與橢圓方程x2+2y2=4聯立.

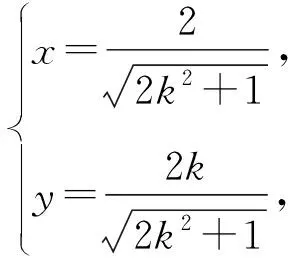
因為點P在第一象限，所以

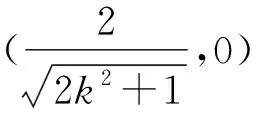
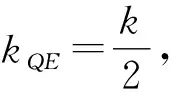
消去y，得

①

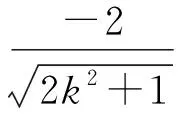
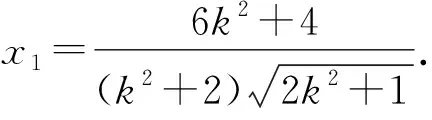
代入直線QE方程中，得

所以點G的坐標為

直線PG的斜率為

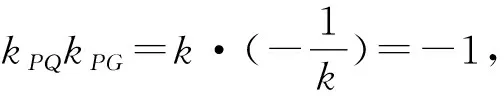
所以PQ⊥PG.

因此△PQG是直角三角形.

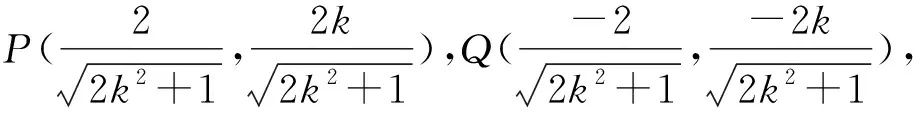
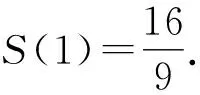
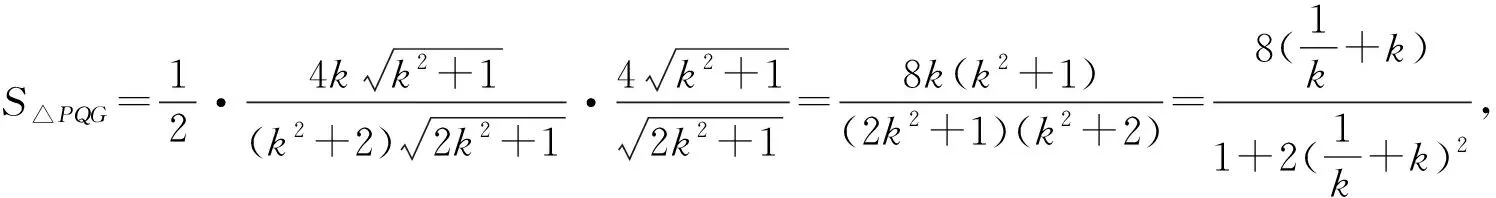
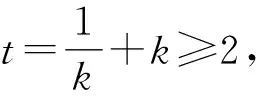
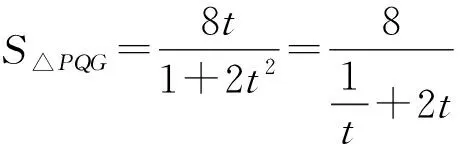
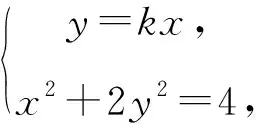
消去y,得(1+2k2)x2=4.

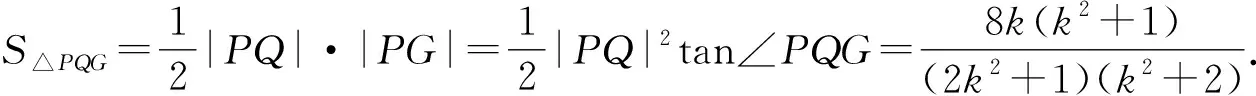
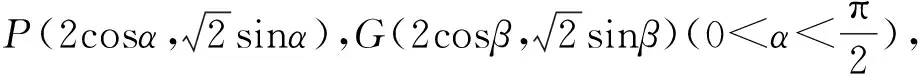
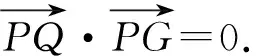
即sin2α+2cos2α=2cosαcosβ+sinαsinβ.

設θ=α-β，則sin2α+2cos2α=2cosαcos(α-θ)+sinαsin(α-θ)=2cosα(cosαcosθ+sinαsinθ)+sinα(sinαcosθ-cosαsinθ)=(sin2α+2cos2α)cosθ+sinαsinθcosα.

故(sin2α+2cos2α)(1-cosθ)=sinαsinθcosα.

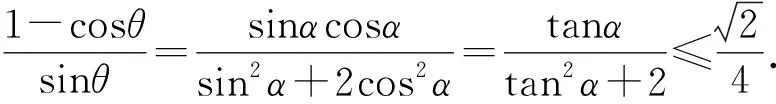
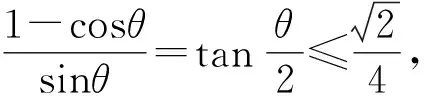
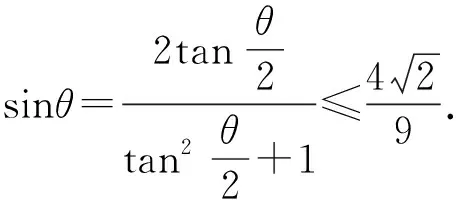
根據坐標系中三角形面積公式得

評注本題解法1比較常規，利用斜率坐標和距離求解，屬于通性通法，解法2對解法1進行了優化運算，利用基本不等式求最值，換元比求導運算量小多了，解法3運用角度和距離求解，不容易想到，解法4利用橢圓參數方程進行三角換元，難度較大，但是利用三角換元求最值有時會起到事半功倍的效果，此題還可以進行仿射變換求解，在此不做贅述.作為壓軸題考查了學生邏輯推理和數學運算能力.

2.2 解決定點(值)問題中的幾個方法

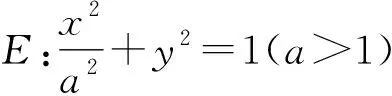
(1)求E的方程；

(2)證明：直線CD過定點.

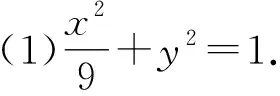
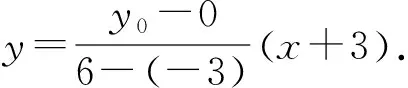
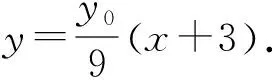
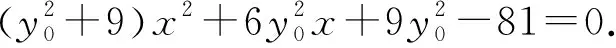
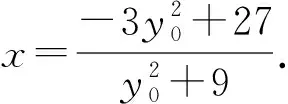
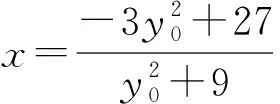
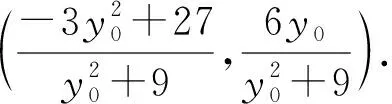
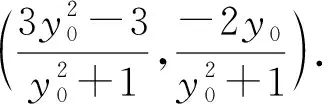
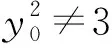
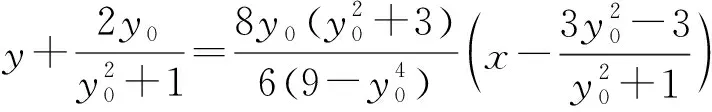
整理,得

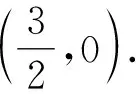
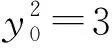
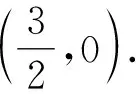
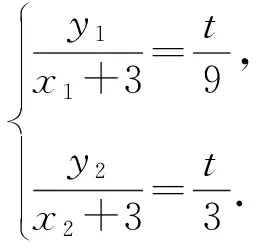
②

③

由②③,得x1y2-3y2y1=-9y1-3y2.

④

由第三定義可知：

則3x1y2-x2y1+3y1-9y2=0.

⑤

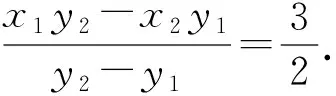
則CD的直線方程為

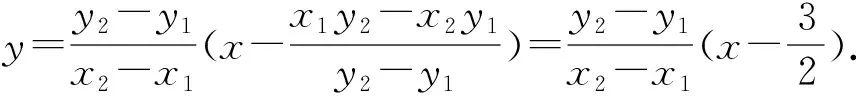
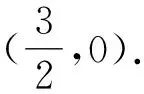
評注本題考查了橢圓的簡單性質及方程思想，計算能力及轉化思想、推理論證能力.也可以利用曲線系和極點極線去解決，由于通性通法比較常用，在此不再贅述.

總結提升(1)求解直線或圓錐曲線過定點問題的基本思路是：把直線或圓錐曲線方程中的變量x，y看成常數，把方程的一端化為零，將方程轉化為以參數為主變量的方程，這個方程對任意參數都成立，這時參數的系數就要全部等于零，這樣就得到一個關于x，y的方程組，這個方程組的解所確定的點就是直線或圓錐曲線所過的定點.(2)求定值問題常用的角度有兩種：一是從特殊值入手，求出定值，再證明這個值與變量無關；二是直接計算、推理，并在計算、推理的過程中消去變量，從而得到定值.

2.3 解決弦長問題的幾個視角

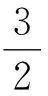
(1)若|AF|+|BF|=4，求l的方程；

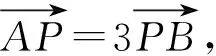
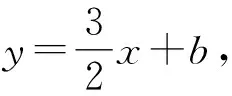
整理,得9x2+12(b-1)x+4b2=0.

故Δ=144(b-1)2-144b2>0.

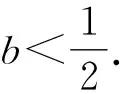
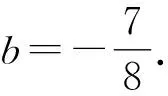
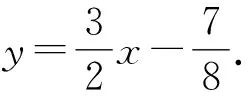
所以y1=-3y2.

整理，得y2-2y+2b=0.

所以y1+y2=2.

解得y1=3，y2=-1.

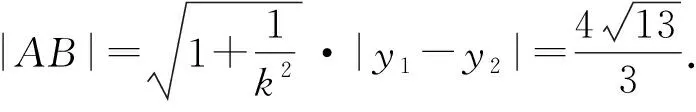
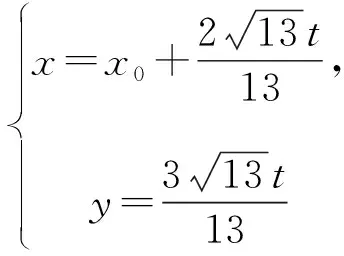
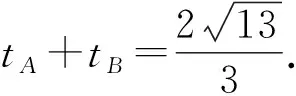
⑥

(1)因為|AF|+|BF|=4，

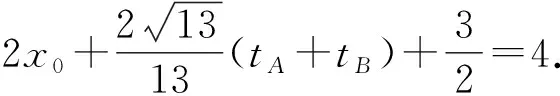
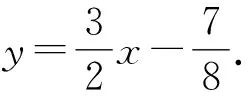
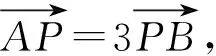
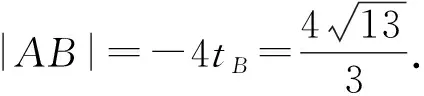
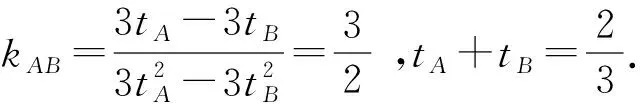
⑦

(1)因為|AF|+|BF|=4，

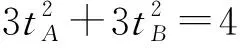
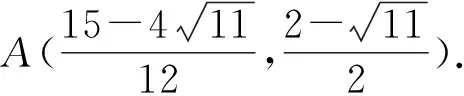
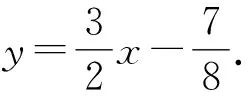
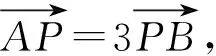
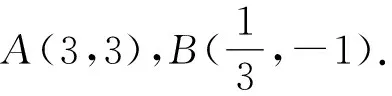
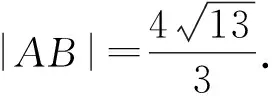
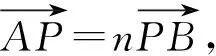
評注本題中利用直線參數方程中參數的幾何意義解題尤其簡單，計算量小，思維量也不大，但是對于學生來說不易想.解決此類問題常用視角有：①通性通法(利用基本概念和性質)；②設直線參數方程法；③設圓錐曲線參數方程法；④極坐標法.

在解答題中以上的總結還遠遠不夠，比如求軌跡方程的常用方法：

(1)直接法：如果動點滿足的幾何條件本身就是一些幾何量，如距離和角的等量關系，或幾何條件簡單明了易于表達，只需要把這種關系轉化為x,y的等式，就能得到曲線的軌跡方程.

(2)定義法：某動點的軌跡符合某一基本軌跡如直線、圓錐曲線的定義，則可根據定義設方程，求方程系數得到動點的軌跡方程.

(3)幾何法：若所求軌跡滿足某些幾何性質，如線段的垂直平分線，角平分線的性質，則可以用幾何法，列出幾何式，再代入點的坐標即可.

(4)相關點法(代入法)：若動點滿足的條件不變用等式表示，但動點是隨著另一動點(稱之為相關點)的運動而運動，且相關點滿足的條件是明顯的或是可分析的，這時我們可以用動點的坐標表示相關點的坐標，根據相關點坐標所滿足的方程，求得動點的軌跡方程.

(5)交軌法：在求動點軌跡時，有時會出現求兩個動曲線交點的軌跡問題，這類問題常常通過解方程組得出交點(含參數)的坐標，再消去參數即可求出所求軌跡的方程.還有關于面積問題、探索性問題等，解析幾何中除了通性通法還有很多視角值得研究，比如彭賽列閉合定理、阿基米德三角形和仿射變換等以高等數學為背景的初等解法值得繼續探究.