多根非線性方程組求解的探路者灰狼算法

逯 苗, 曲良東, 何登旭

(廣西民族大學數(shù)學與物理學院，南寧 530006)

0 引言

非線性方程組是數(shù)學學科中的一個重要組成部分[1–2]，在現(xiàn)實生活中，很多物理[3]、工程[4]類問題最后都可歸結為非線性方程組的求解問題。因此，對求解非線性方程組，尤其是多根非線性方程組的研究具有重要研究意義。目前有很多應用傳統(tǒng)的方法對多根非線性方程組求解，比如：牛頓法[5]、迭代法[6]等。但傳統(tǒng)算法對迭代初始值的選取比較嚴格，或需要計算導數(shù)和矩陣求逆，對于有些復雜的方程組不存在導數(shù)或很難求解時，這些算法就產(chǎn)生一定的局限性，即使找到方程組的近似解，但是精度較差[7]。

隨著群智能算法應用領域的不斷被擴充，群智能算法被廣泛應用到求解多根非線性方程組，在求解問題時，首先將多根非線性方程組問題轉化為優(yōu)化問題，即轉化成單目標優(yōu)化問題或多目標優(yōu)化問題兩種方法。近年來，Pourrajabian 等[8]將遺傳算法和增廣拉格朗日函數(shù)進行結合求解簡單非線性方程組。Ali 等[9]利用差分進化算法結合精英反向學習以及變步長隨機定位的概念等，提出了求解多目標優(yōu)化問題的改進差分進化算法。王冬冬和周永權[10]將人工魚群算法應用于非線性方程組的求解問題。歐陽艾嘉等[11]將Hooke-Jeeves 算法與粒子群算法結合提出求解非線性方程組的混合粒子群優(yōu)化算法。趙光偉和周永權[12]提出人工螢火蟲算法和復合形法相結合的方法求解非線性方程組的問題。Abdollahi 等[13]采用帝國主義競爭算法求解非線性方程組等。

群智能算法具有結構簡單，收斂速度快。因此，將群智能優(yōu)化算法應用于非線性方程組求解時對初始解要求不高，不需要進行求導，而且具有較強的魯棒性。但在多根非線性方程組的求解過程中仍然存在求解個數(shù)不完全、精度不高等問題。為解決這一問題，本文提出探路者灰狼優(yōu)化算法，受探路者算法中跟隨者的啟發(fā)，對灰狼種群中β、δ、ω個體位置的更新原則進行改變；重新設計位置更新公式等對原灰狼算法進行改造，進而對多根非線性方程組進行求解，通過仿真實驗以及和其他智能算法的比較，進一步驗證該算法在多根非線性方程組的求解問題上有良好的求解效果。

1 非線性方程組

設一個非線性方程組由n個方程組成，涉及n個未知量，形式如下

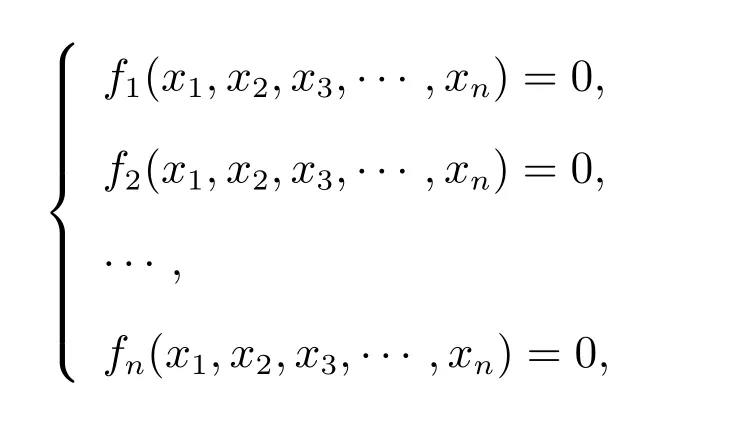
其中fi(X) =Ai(i= 1,2,··· ,n)為非線性方程組，X= [x1,x2,··· ,xn]為方程組的未知向量，Ai(i= 1,2,··· ,n)為常數(shù)項。群智能優(yōu)化算法在求解非線性方程組的問題時，需要將非線性方程組問題轉換為優(yōu)化問題。將非線性方程組轉化為單目標優(yōu)化問題，其表達形式為

那么求非線性方程組的解的問題就轉化成了求適應度函數(shù)F(X)最小值的問題。本文選取公式(1)的方法求解非線性方程組的解。

2 灰狼優(yōu)化算法和探路者算法

2.1 灰狼優(yōu)化算法

灰狼優(yōu)化算法(Grey Wolf Optimiztion, GWO)[14]是一種新型群智能優(yōu)化算法，主要模擬灰狼的社會等級和捕食行為。種群中的頭狼稱為α，其次為β，然后是δ，其余狼稱為ω。在求解函數(shù)優(yōu)化問題時，假設灰狼種群規(guī)模為N，搜索維度為d維，xi=(xi1,xi2,··· ,xid)用來表示第i只灰狼在d維空間的位置，它們對獵物的搜索行為可以通過以下數(shù)學模型進行描述

其中Xp(t)表示第t代獵物的位置；X(t)表示第t代灰狼個體的位置；常數(shù)C為擺動因子，由式(5)決定，A為收斂因子，由式(6)決定

其中r1和r2是取值在[0,1]之間的隨機向量，a在迭代中從2 線性地減小到0。

對于每一只ω狼，首先根據(jù)

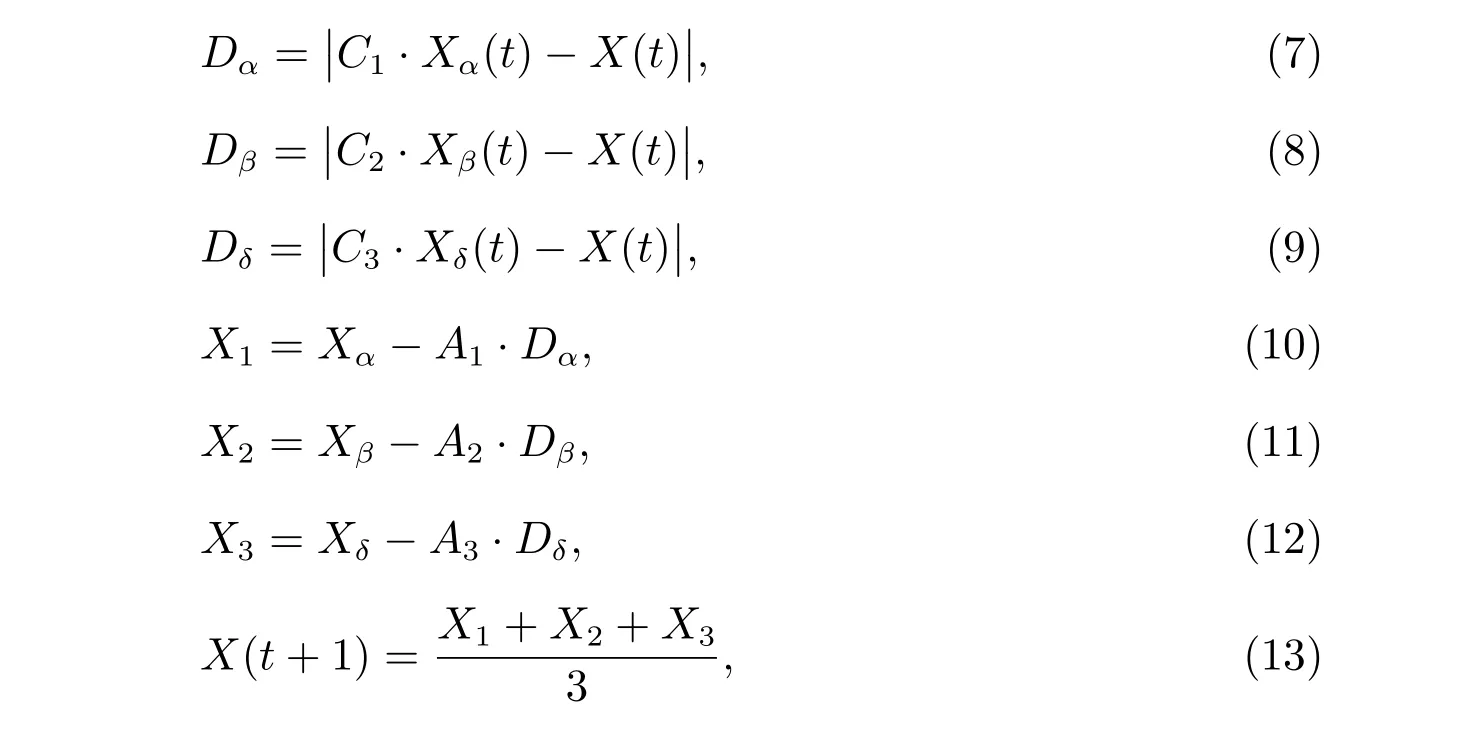
計算它們與α、β、δ的距離，然后由式(13)綜合判斷出灰狼個體向獵物移動的方向。Xα表示α狼的位置，Xβ表示β狼的位置，Xδ表示δ狼的位置，C1、C2、C3是隨機向量。

2.2 探路者算法

探路者算法(Pathfinder Algorithm, PFA)[15]受到動物群體運動的啟發(fā)，模仿動物群體的領導階層來尋找最佳的食物區(qū)域或獵物。每個個體在空間中都有一個位置，種群中的最優(yōu)位置將被選為領導者，這里我們稱種群的領導者為探路者，種群中的其他個體稱為跟隨者，到尋找獵物或覓食區(qū)域時，個體將跟隨探路者，則探路者的更新公式如下

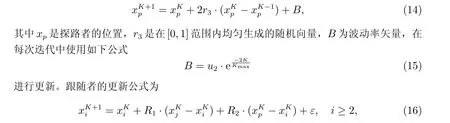
其中K表示當前迭代，xi是第i個成員的位置向量，xj是第j個成員的位置向量，R1和R2是隨機向量，R1=αr1, R2=βr2，r1和r2是在[0,1]范圍內均勻生成的隨機變量，α是相互作用系數(shù)，取值為α= 1+(2?1)·rand，β是與探路者保持的隨機距離，取值為β=1+(2?1)·rand，ε是振動向量，使用如下更新公式

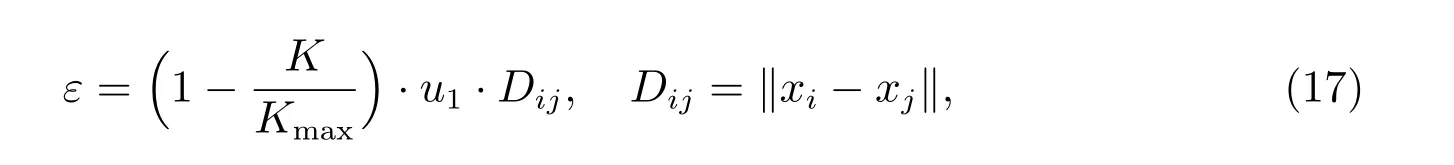
其中u1和u2是在[0,1]的隨機數(shù)，Dij是兩個成員之間的距離，Kmax是最大迭代次數(shù)。

3 多根非線性方程組求解的探路者灰狼算法

3.1 探路者灰狼算法(PGWO)

灰狼優(yōu)化算法和探路者算法從算法結構上講，兩個算法都有領導者和跟隨者，灰狼主要由α狼進行引導使其他等級的狼向獵物展開攻擊圍捕。因此，α狼對應看作是探路者，β狼則是α狼的跟隨者，δ狼的位置由α狼、β狼決定，可以看作跟隨者。兩種算法進行結合在原理上具有一定優(yōu)勢，由于GWO 算法后期收斂速度慢，原因在于狼群主要依據(jù)與α、β和δ的距離來判斷與獵物之間的距離所導致。而在PFA 算法中，跟隨者的更新機制可以有效解決這一問題，具有較好的平衡算法的全局搜索和局部開發(fā)的能力。PGWO 算法將保留α狼的更新原則，對其余灰狼的更新將結合跟隨者的更新原則對原過程進行修改。這樣即保留了全局搜索能力，又提高了局部開發(fā)能力，增強探測能力的同時提高收斂速度和精度。

α狼的位置按照GWO 算法中的更新公式(7)、(10)進行更新，β狼作為α狼的跟隨者，為最優(yōu)的跟隨者，β狼的位置更新將直接由與α的距離決定，位置更新如下

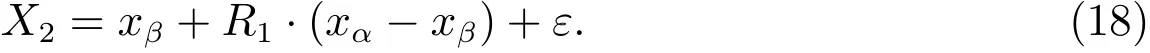
δ狼作為α和β狼的跟隨者，是次優(yōu)的跟隨者，位置更新由α和β，β和δ的距離決定，位置更新如下

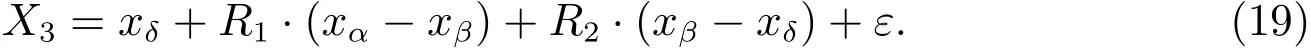
其他灰狼的位置更新如下

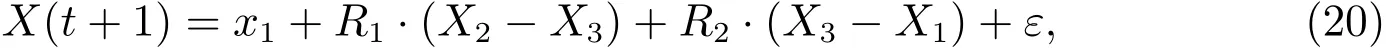
其中C、A分別按照公式(5)和(6)進行更新，ε按照公式(17)進行更新。探路者原算法中跟隨者的位置由任一位置和最優(yōu)位置的距離決定的，而改進的GWO 算法中跟隨者的位置由最優(yōu)跟隨者和探路者決定，可以提高算法的局部搜索能力，提高搜索精度。

3.2 算法步驟

多根非線性方程組的求解就是將問題轉化為最優(yōu)化問題，由于傳統(tǒng)算法的局限性和復雜性，一般群智能算法在多根問題的求解存在求解個數(shù)不全以及精度不高的問題。本文提出探路者灰狼算法，相比較原始灰狼優(yōu)化算法結合了探路者算法的探路者和跟隨著的更新機制，并對位置更新機制進行更改，有效提高算法的收斂速度以及搜索精度，具體算法描述如下：

步驟1 參數(shù)設置，種群規(guī)模N，最大迭代次數(shù)Tmax，搜索維度D，搜索范圍[lb,ub]以及A、C、ε；

步驟2 初始化種群個體，并計算灰狼個體的適應度值，保存適應度值最好的前三匹狼記為α、β、δ；

步驟3 根據(jù)公式(7)和(10)對α狼的位置進行更新，再根據(jù)公式(18)和(19)分別更新種群中β、δ狼的位置，根據(jù)公式(20)更新當前灰狼位置；

步驟4 根據(jù)公式(5)和(6)更新參數(shù)A、C，再根據(jù)公式(18)更新參數(shù)ε；

步驟5 判斷是否滿足結束條件，若滿足輸出結果，即為最優(yōu)灰狼位置，否則返回步驟3。

4 仿真實驗與結果分析

為了測試PGWO 算法的多根非線性方程組求解的性能，采用9 個方程組作為測試方程組，并且和其他實驗數(shù)據(jù)加以比較。在對比實驗中，為保證算法的公平性，所有的仿真實驗實現(xiàn)在CPU 為Intel Core i7-10510u，主頻為1.80 GHz，內存為8 GB 的PC 上，采用Matlab R2018(b)進行實現(xiàn)。

實驗1 選取參考文獻[16]中的方程組1、方程組2，參數(shù)設置為：種群規(guī)模N=30，最大迭代次數(shù)1 000，獨立運行30 次，計算其平均值，實驗結果如表1。

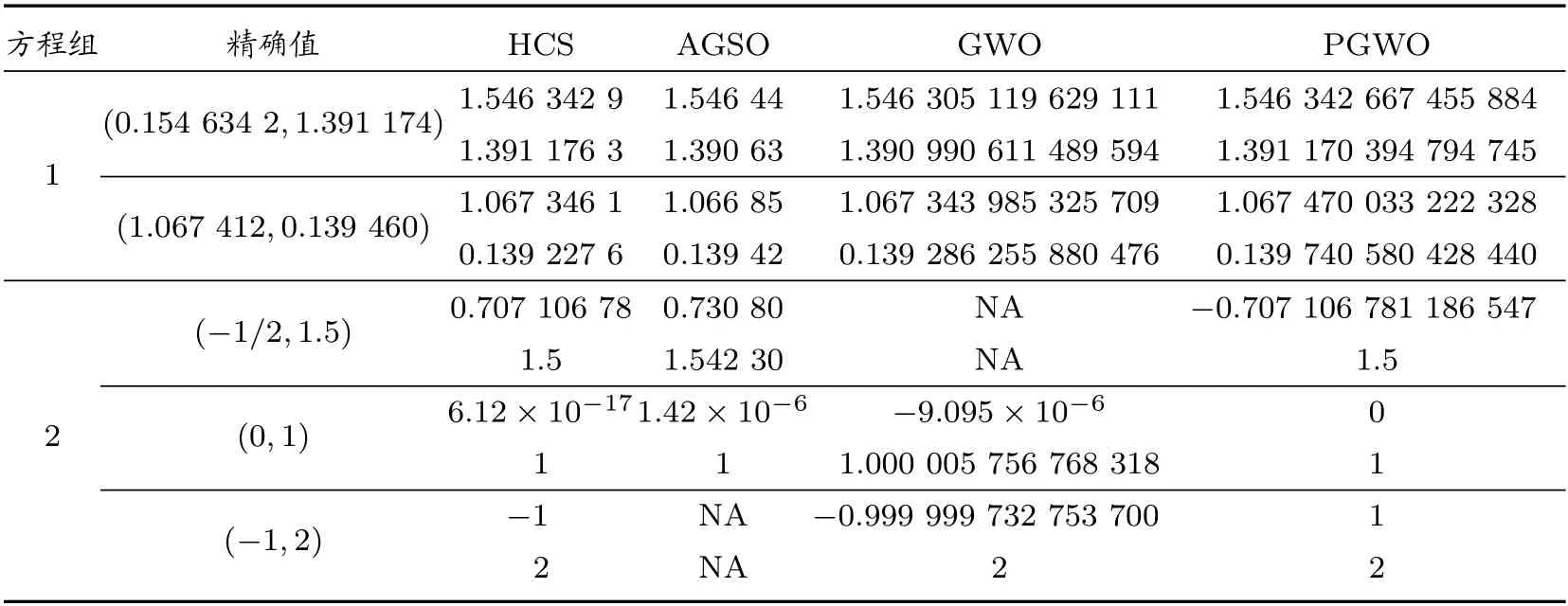
表1 方程組1、方程組2 的計算結果

方程組1

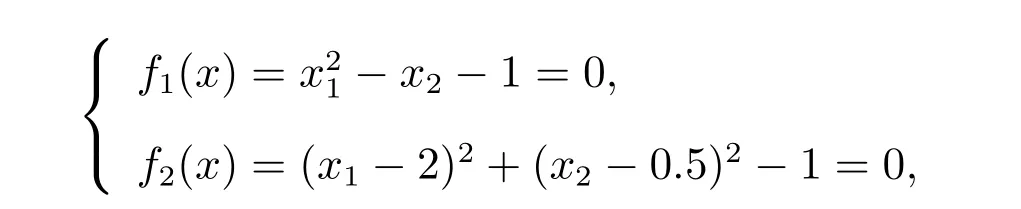
其中x ∈[0,2]，理論解為x?=(1.546 342,1.391 174)T, x?=(1.067 412,0.139 460)T。

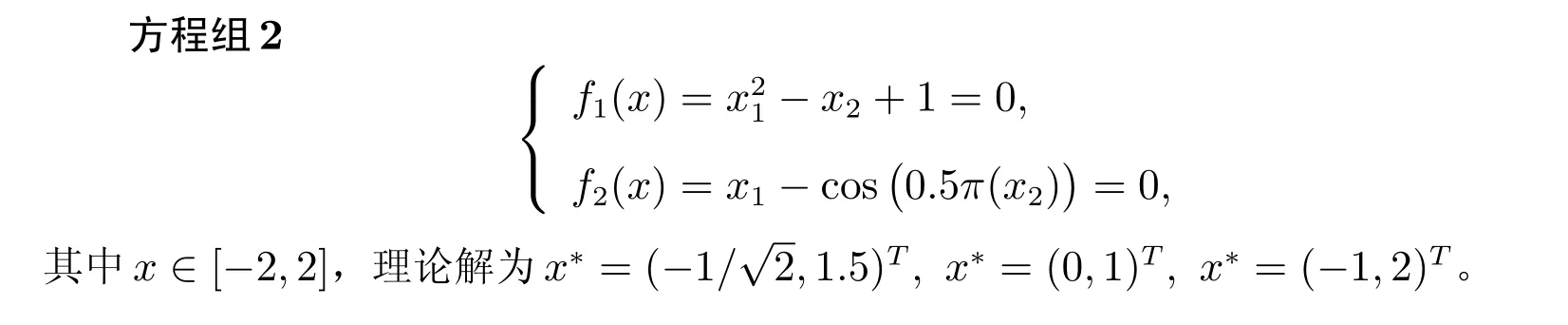
由表1 可知，NA 表示未求出的解，對于方程組1，PGWO 算法能求出全部解，比HCS 算法和文獻[17]中的AGSO 算法求解精度高，并且求解精度優(yōu)于原始灰狼優(yōu)化算法。對于方程組2，AGSO 算法和GWO 算法只能求出兩個解，求解不全，PGWO 算法求得全部解并且求解精度優(yōu)于HCS，說明利用此算法能更大程度地獲得問題的解。

實驗2 選取文獻[16]中的方程組9、方程組10 進行比較分析，為了方便比較，參數(shù)設置為：種群個數(shù)100，最大迭代次數(shù)5 000，Pa= 0.25, F= 0.6, CR= 0.8，每個方程組獨立運行50 次，求其平均值，實驗結果如表2 和表3 所示。

方程組3

從表2 和表3 可知，方程組3 用本文算法求出的結果比理論值精度高，但x2比HCS 算法的精度略差，與標準GWO 算法和AGSO 算法相比求解精度高。方程組4 的測試結果與理論值、HCS、AGSO 算法比較發(fā)現(xiàn)PGWO 算法能求出全部解并且求解精度較高。

表2 方程組3 的計算結果

實驗3 選取參考文獻[18]中的例1、例4、例5 進行測試分析，以及文獻[19]中的F36、F52。參數(shù)設置為：種群個數(shù)100，最大迭代次數(shù)1 000，每個方程組獨立運行50 次，求其平均值，實驗結果如表4 至表6 所示。

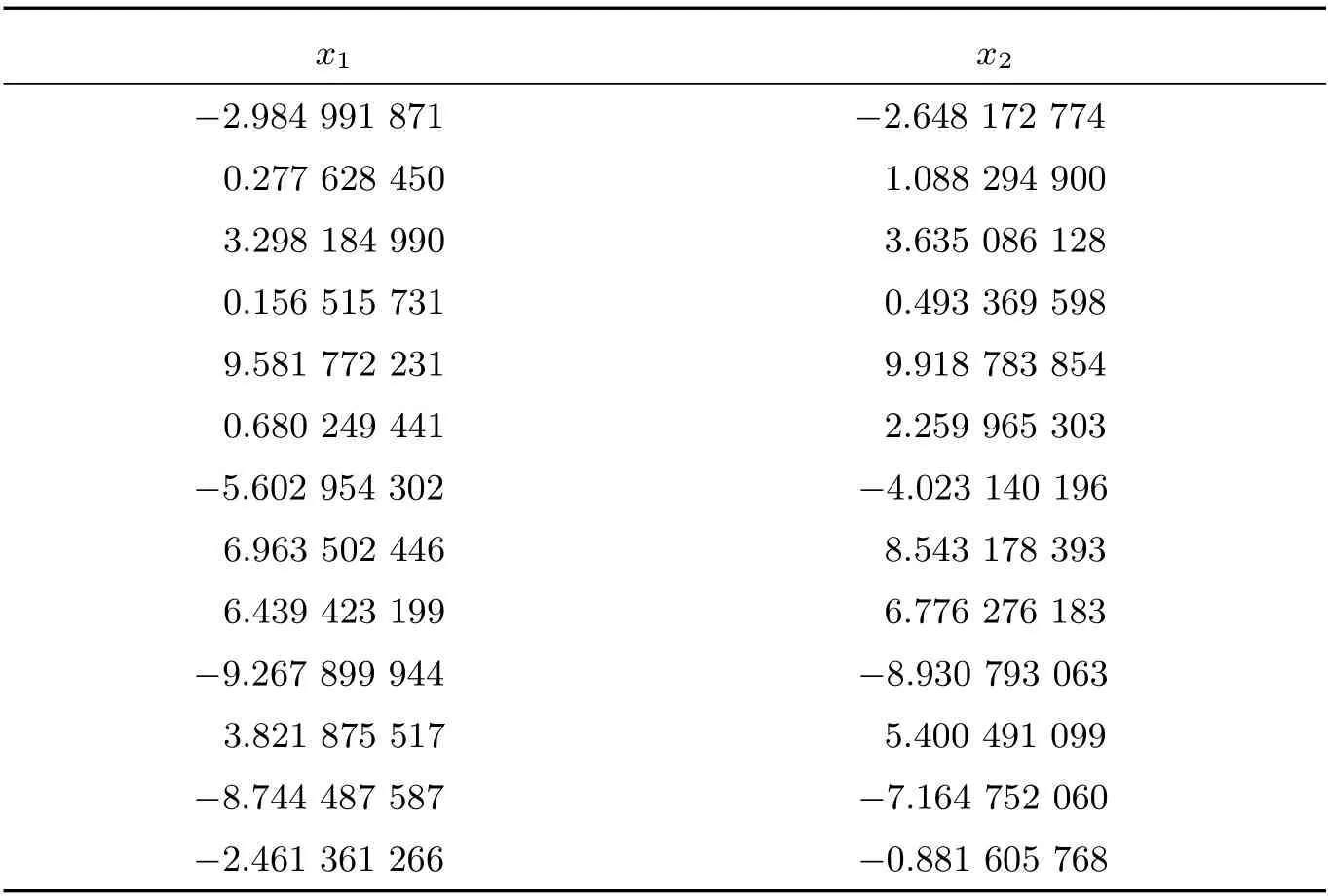
表4 方程組5 的計算結果

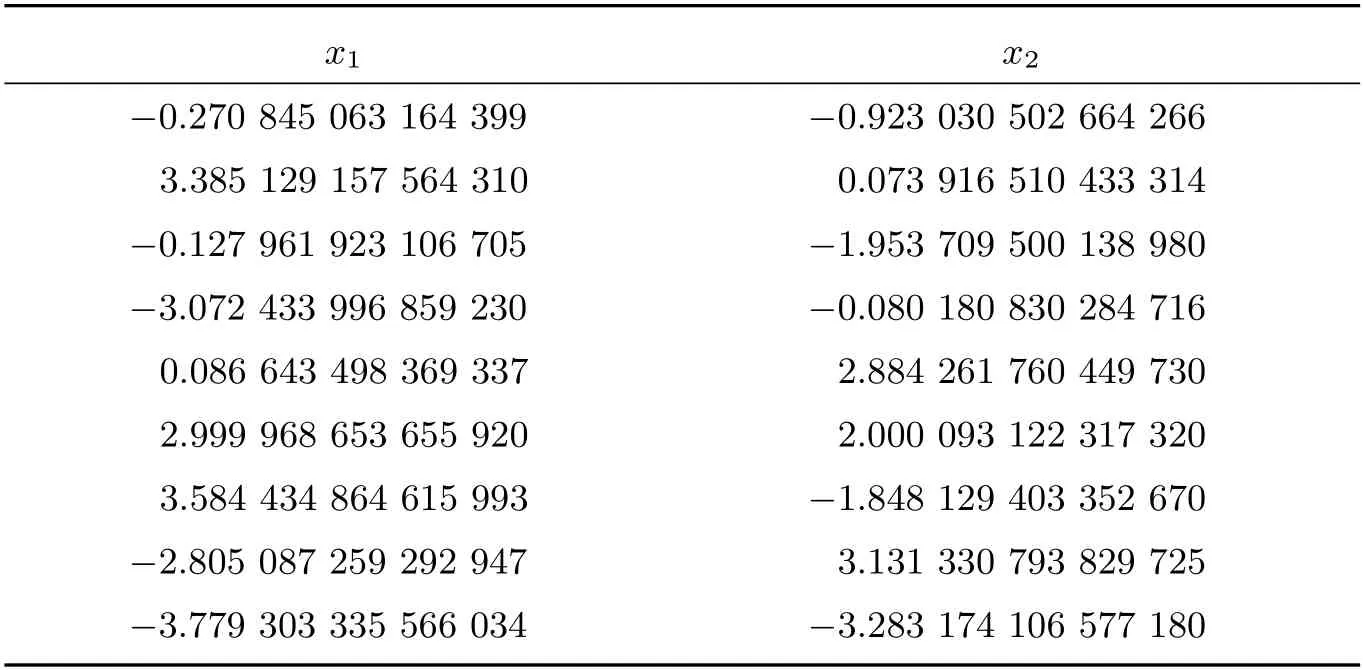
表6 方程組7 的計算結果

方程組5

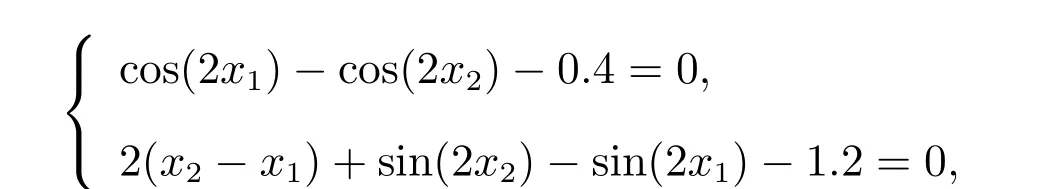
其中xi ∈[?10,10]，該方程有如下13 個解：

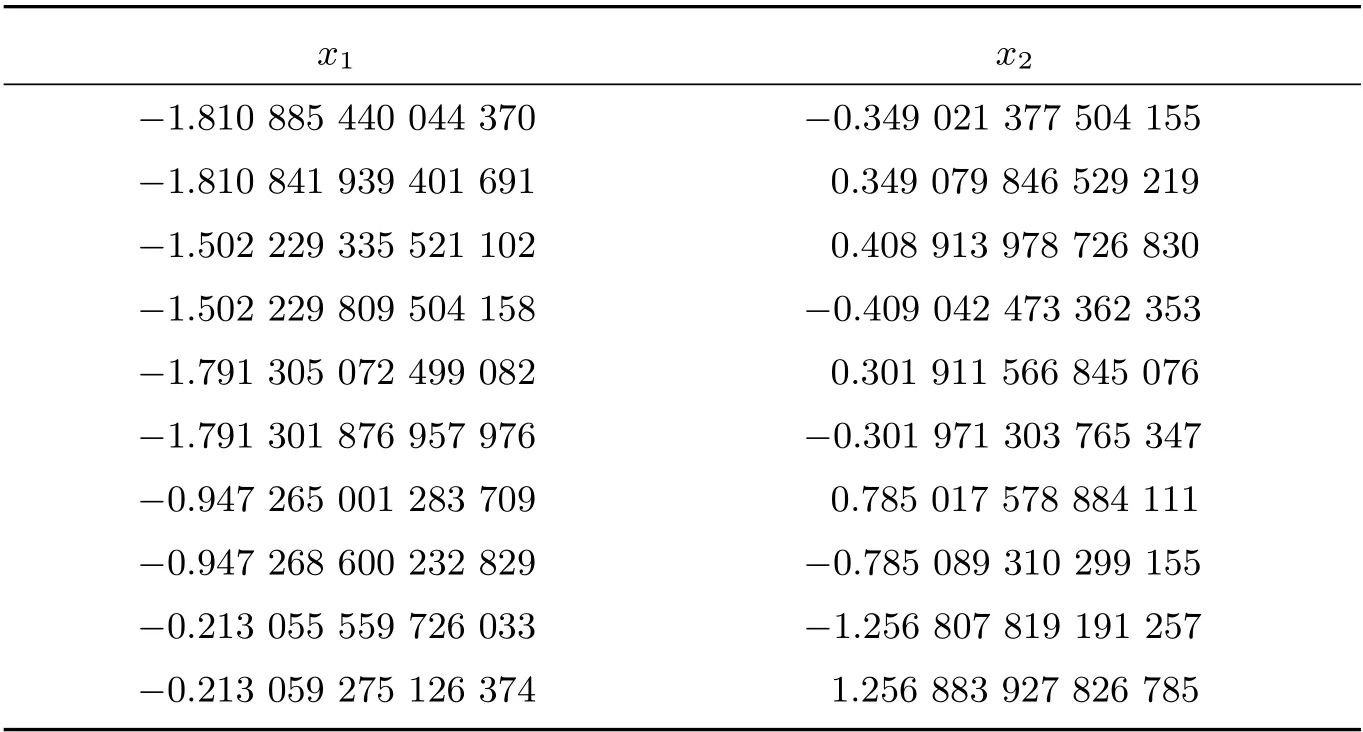
表5 方程組6 的計算結果

方程組7

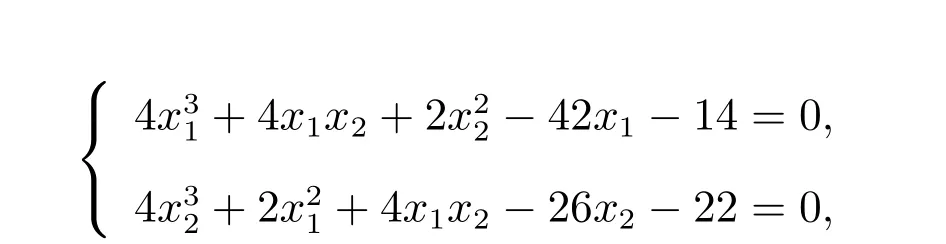
其中xi ∈[?5,5], i=1,2，該方程有如下9 個解：

根據(jù)以上方程組可知，方程組5 有13 個解，HCS 算法求出9 個解，AGSO 算法求出8 個解，GWO 算法求出10 個解。方程組6 有10 個解，HCS 算法求出10 個解，AGSO算法求出8 個解，GWO 算法求出10 個解，但求解精度較PGWO 算法稍差。方程組7 有9個解，HCS 算法求出7 個解，AGSO 算法求出5 個解，GWO 算法求出7 個解，對于這三個多根的方程組，由表4 至表6 可知，PGWO 算法可以求出全部解并且求解精度較高，說明該算法在迭代范圍內能求出全部解，PGWO 算法在多根非線性方程組的求解問題中具有較強的搜索能力。

方程組8

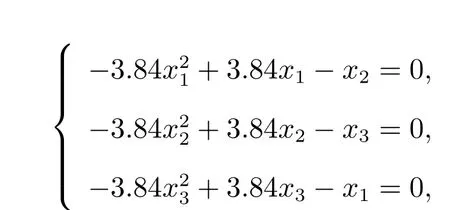
其中xi ∈[0,1], i=1,2,3，該方程有如下8 個解：

方程組8 有8 個標準解，從表7 中數(shù)據(jù)顯示，PGWO 算法求出7 個精度較高的解，而HCS 算法和AGSO 算法均求出6 個解，GWO 算法求出7 個解。方程組9 有15 個標準解，從表8 中數(shù)據(jù)顯示PGWO 算法求出14 個精度較高的解，而HCS 算法和AGSO 算法均求出13 個解，GWO 算法求出14 個解。根據(jù)以上8 個多根測試方程組的實驗結果可以看出，在求解多根方程組1 至方程組4 時，PGWO 算法的求解性能相對其他群智能算法比較明顯，足以說明GWO 算法和PFA 算法融合對多根非線性方程組求解的高效性。對于多根方程組5 至方程組7 的求解，PGWO 能夠求出全部解且求解精度較高。但是從方程組8、方程組9 的數(shù)據(jù)顯示，PGWO 算法在求解個別多根的非線性方程組是依然存在求解不完全的問題，該問題也會成為進一步改進的重點。

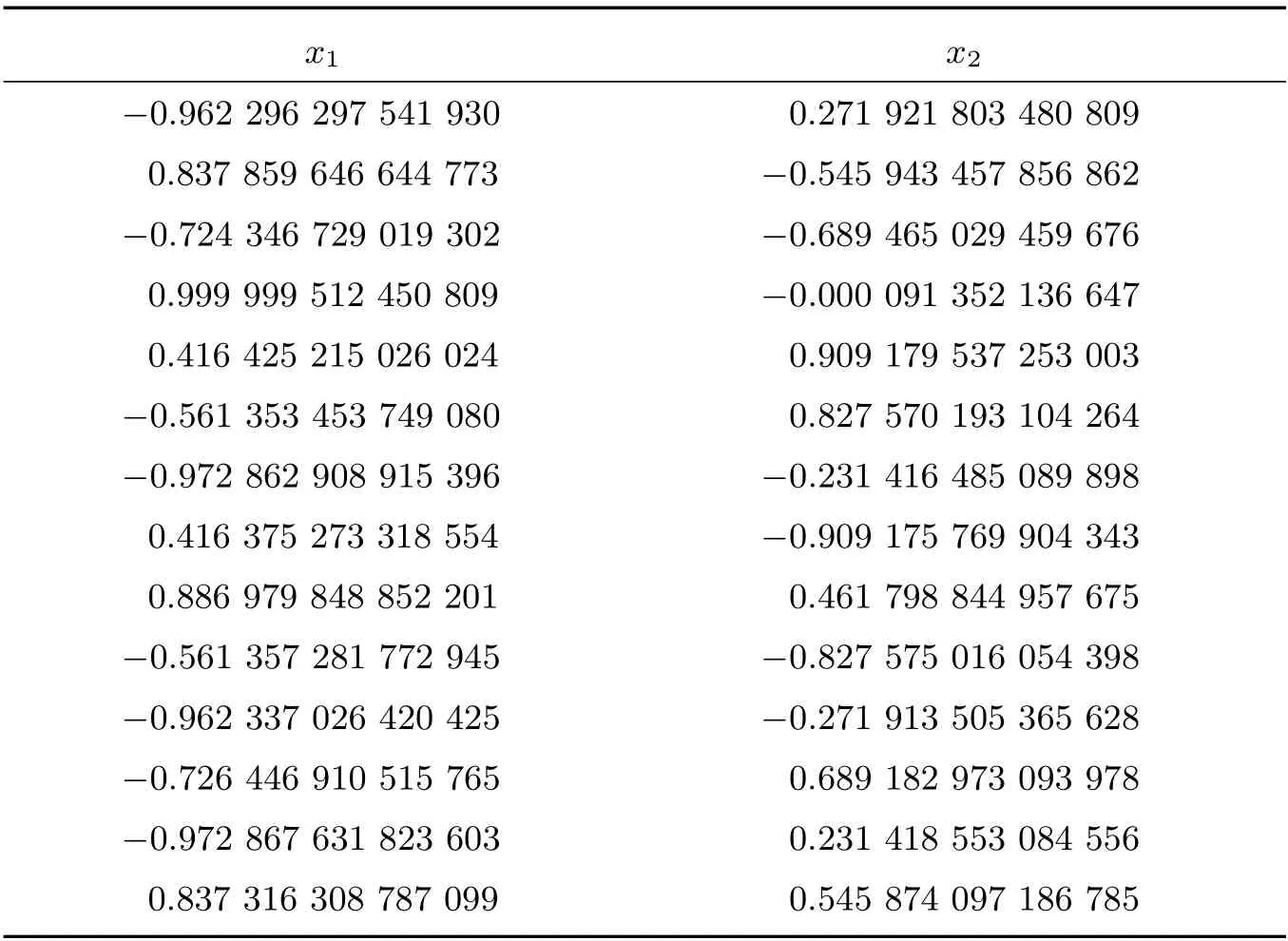
表8 方程組9 的計算結果

5 結論

本文分析了傳統(tǒng)多根非線性方程組求解方法的不足，并提出了一種結合探路者算法中跟隨者更新機制的灰狼優(yōu)化算法。通過9 組測試方程組進行了反復實驗，并與其他智能優(yōu)化算法進行比較分析，最后實驗數(shù)據(jù)表明，本文算法在求解的精度上都具有一定優(yōu)勢，但是對于個別多根非線性方程組的求解存在求解不完全的現(xiàn)象。接下來將針對該算法進行深入研究，并應用到其他領域。