診斷學生學習起點,搭建思維進階階梯
明雨


【摘? ?要】開展學情調研能夠全面了解學生的已有知識經驗和認知水平。教師以“比例的應用”一課為例,通過“分析學情調研作品,明晰學生學習起點;依托典型調研作品,設計核心學習任務;用好差異調研作品,驅動學生深度思考”等調研活動,為學生搭建思維進階階梯,發展比例推理能力。
【關鍵詞】比例的應用;學情調研;比例推理
學情調研是單元教學研究的重要一環。開展學情調研,能夠全面了解學生的學習起點,為課堂教學設計與實施提供科學、精準的依據和保證,從而幫助學生在單元學習過程中,實現核心素養和關鍵能力的不斷進階。近年來越來越多的一線教師根據自己的教育經驗意識到學情調研的重要性[1]。但是,在具體實踐中,也存在如下問題:一是“想當然”的經驗主義,教師利用自己的教學經驗對學情“想當然”地進行推斷;二是以教材分析取代學情分析的本本主義;三是學情描述與整體教學內容、教學設計相互割裂的“兩張皮”[2]。那么,如何開展學情調研,診斷學生的學習起點?怎樣把學情調研融入課堂教學中去,為學生搭建思維進階的階梯?
一、分析學情調研作品,明晰學生學習起點
分析學情調研作品,教師能夠從學生的實際情況入手,把握教學內容,設計有針對性的學習任務。“比例的應用”在認識“比例的意義”和“比例的基本性質”的基礎上進行教學,通過應用比例解決生活中的數學問題,加深學生對比例意義的理解。按照語義結構,Lamon[3]將“比例的應用”中的解決問題歸類為“自定義關系的量”,具體指的是量與量之間是人為制定的一種關系,如3個小孩配1個大人,4個瓶蓋換1瓶汽水等。在前期學習的基礎上,學生在解決“自定義關系的量”這類比例問題時會用到哪些策略?解決問題的過程中會遇到哪些困難?在開展教學活動之前,教師對學生進行了如下調研。
調研目的:了解學生解決“自定義關系的量”問題的方法和困難。
調研對象:B市H區Z校六年級12班37人。
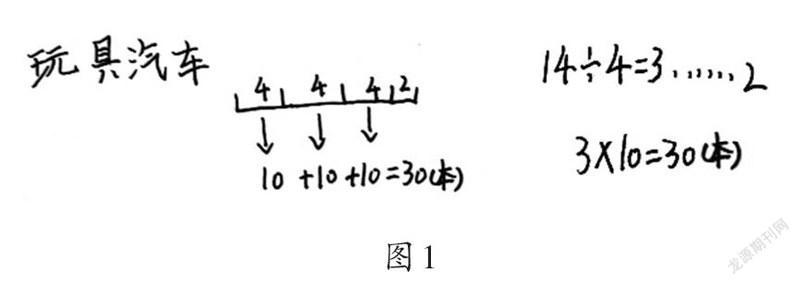
調研題目:人們有時候使用“物物交換”的方式,按照一定的比例交換自己所需的物品。14個玩具汽車可以換多少本小人書?你可以用畫一畫、算一算來解決問題。
從調研結果來看,學生作品呈現多樣化特征。學生解決問題的策略有畫圖、列表、列式和方程。教師試圖利用學情調研作品,對學生思維水平進行分層歸類,明晰學生思維的起點;從不同的解答方法中,找出學生的認知難點。
(一)從分類到分層:了解學生思維現狀
比例推理是根據已有的數量信息并依照比例的特性,判斷比例是否成立的過程[4]。學生采用什么樣的解決問題策略是由他們的知識、經驗水平決定的。結合本次學情調研的作品情況,本文將根據學生解決問題的策略將作品分為“不能建立比例關系、集合策略、單價比策略和雙復合乘法操作策略”四類,并通過分析將學情調研作品分層,明確不同水平學生的認知起點,設計更有針對性的學習活動。
1.不能建立比例關系的有4人,典型作品如圖1所示。
2.采用集合策略的有3人,這里的集合策略是指在一個比的基礎上,通過加法運算將這種關系擴展到第二個比中。典型作品如圖2所示。
3.采用單價比策略的有25人,所謂單價比策略是指先找出單位比,再根據單位比進行推斷,這種方法屬于前比例概念階段。典型作品如圖3所示。
4.采用雙復合乘法操作策略的有5人,采用這一方法的學生對數值間的比例關系有深刻的理解,操作水平在更高層次上形成了穩定的格局[5]。典型作品如圖4所示。
除此之外,同一比例問題可以有“內在比”和“相間比”兩種解決問題的角度,“內在比”是指同一情境下的比,如調研題目中的4個玩具汽車換10本小人書,“相間比”是指同一類事物不同狀態下的比,如調研題目中的14個玩具汽車和4個玩具汽車的比[6]。通過分析學生調研作品,對學生解決問題策略進行分類,可更加明晰學生比例推理能力的不同水平。
(二)從個性到共性:找準學生認知難點
如何引導不能建立比例關系、使用集合策略和單價比策略的學生掌握雙復合乘法操作的策略,實現比例推理能力的進階?通過分析學生比例推理的四種水平,能夠發現學生的認知難點。其中不能建立比例關系的學生,只能根據題目描述建立4個玩具汽車和10本小人書的對應關系,沒有得出2個玩具汽車兌換5本小人書的比例關系。學生在使用集合策略和單價比策略時,都需要獨立解決用剩余的2個玩具汽車兌換5本小人書的問題,最后與成整倍數兌換的小人書相加(如圖5)。
通過分類分析發現,解決問題的關鍵是找出2個玩具汽車可以兌換5本小人書的數量對應關系,并以此建立比例,進行關系推理。
二、依托典型調研作品,設計核心學習任務
充分利用學情調研作品,以學生的思維水平為基礎,設計核心學習任務,可以更好地在課堂呈現學生真實的思考,促進學生的知識建構與素養的形成,把不同思維水平的學生都帶入有效的學習中。
(一)從作品到素材:撬動學生的思考
如何基于學情調研設計學習任務,通過呈現不同水平學生的作品,引導每一個學生參與課堂學習?教師首先要創設真實情境,介紹人們在現實生活中的交換商店中可以通過以物易物兌換舊物、玩具、書籍等。接著呈現數學信息和問題“14個玩具汽車可以換多少本小人書?”為了讓學生明晰學習任務,教師提供學習任務和學習建議。
學習任務一:14個玩具汽車可以換多少本小人書?
學習建議:
1.你可以用畫一畫、算一算的方法,在學習單中記錄你的想法。
2.完成后和同桌講一講你是怎么想的。
學生通過獨立思考,記錄解決問題的過程和結果,教師結合學生的典型作品和學情調研的分層情況,展示兩個學生的典型作品(如圖6)。其中左邊作品呈現的是沒有建立比例關系的錯例,作品只建立了玩具汽車和小人書的對應關系,沒能建立兩者的比例關系,代表比例推理水平較低的學生的思考;右邊作品先建立了玩具汽車和玩具汽車的倍數關系,得到單位比,再得到小人書的數量。展示作品后,教師提出問題:“你能讀懂哪位同學的方法?還有什么問題和補充嗎?”
通過創設真實情境,提出數學問題,學生調用已有學習經驗,用多種方法解決問題。呈現典型的、不同水平的學生作品,為生生交流、師生交流提供了資源和素材。學生應用“內在比”和“相間比”這兩種比例關系解決問題,體會到解決問題方法的多樣性。
(二)從零散到關聯:發展比例推理能力
知識理解的本質是將新知識和已有知識建立有聯系的、個性化的認識結構。如何設計學習任務,以幫助學生建立已有方法和比例方程之間的本質聯系,使用雙復合乘法操作的策略解決問題,促進比例推理能力的進階?在教學中,教師引導學生用比例方程解決問題。在學生獨立思考后,教師展示學生作品(如圖7)。其中方法③建立了玩具汽車和小人書之間的“內在比”;方法④建立了玩具汽車和小人書之間的“相間比”。
為了讓學生的交流有的放矢、聚焦數學本質,教師出示如下學習任務。
學習任務二:請你解釋這樣列式解決問題的道理。
學習建議:
1.小組合作,說一說,比例式兩邊的比分別表示什么意思。
2.整體觀察四種解決問題的方法,你又有什么新發現?
在每個學生都獨立嘗試用比例解決問題的基礎上,小組合作進一步理解兩種比例方程,加深對“內在比”和“相間比”兩種比例關系的理解,使用雙復合乘法操作的策略解決問題,實現比例推理能力的進階。
三、用好差異調研作品,驅動學生深度思考
在課堂教學中,學生原有的個體差異是教學活動的起點或前提,這種差異也可以作為一種教學資源。充分利用學生的差異作品, 在貼近學生思維水平的基礎上,引導學生獨立思考、交流辨析、反思質疑,能夠有效地促進學生深度思考,提高課堂學習效率。
(一)讓錯誤作品成為辨析的錨點
學生的錯誤作品是寶貴的學習素材。課堂教學中,呈現學生的真實作品,更能引起學生的共鳴。一個錯誤作品能代表一類學生的錯誤認知表現。通過對錯誤作品的剖析,不僅能夠充分調動學生的學習交流興趣,而且能在討論思辨中加深學生對數學本質的理解。本節課的第一個學習任務,教師將不能建立比例關系的錯誤作品呈現在黑板上,如圖7方法①所示,引發學生的交流討論。
生:此方法是錯誤的,因為2個玩具汽車還能兌換5本小人書。
生(畫圖學生):不夠4個玩具汽車不能兌換呀!
師:你很有生活經驗,如果我們從數學的視角來思考,這2個玩具汽車可以兌換多少本小人書呢?
生:4個玩具汽車可以兌換10本小人書,那么2個玩具汽車就能兌換5本小人書。你們看4除以2等于2,10除以2等于5。
生:我們也可以圈一圈、分一分,4個玩具汽車兌換10本小人書,平均分一下,2個玩具汽車就兌換5本小人書。
生(畫圖學生):我知道了,玩具汽車的數量變成了2,小人書的數量就變成了5,但是玩具汽車和小人書之間的比值是不變的。
師:同學們真了不起,能夠用不同的方法說明2個玩具汽車兌換5本小人書的道理,我們也要感謝畫圖的同學,為我們提供了交流討論的資源,同時,我們也看到了他在學習過程中的收獲,就是兌換過程中玩具汽車和小人書的比值是不變的。
課堂中營造討論的氛圍能夠讓學生充分地交流自己的思考過程。通過對錯誤作品的討論和辨析,引導沒有建立比例關系的學生進一步思考兩個量之間的關系,進而明晰玩具汽車和小人書之間的比值是不變的。在充分辨析的基礎上,進一步建立畫圖方法和列算式方法之間的聯系,引導學生從形象思維過渡到抽象思維的算式表達。
(二)把多樣作品作為對比資源
對比多樣作品,發現不同方法之間的區別和聯系,能夠進一步加深學生對數學本質的理解。教學過程中,教師通過設計學習任務,引導學生觀察課堂中重點討論的四種解決問題的方法,如圖7所示。學生經歷整體觀察、小組交流后,全班分享談發現。
生:我可以把上面的四種方法分分類,方法①和方法②是一類的,都是建立了玩具汽車和小人書之間的關系,方法③和方法④是一類的,玩具汽車和玩具汽車的比值與小人書和小人書的比值是相等的。
師:雖然解決問題的形式不一樣,但是建立的比例關系是相同的,抓住方法的本質能夠更好地解決問題。
生:我把兩種用比例方程解決問題的方法分為一類,因為它們都可以直接用比例的性質來解決。
師:的確,正確列比例方程,根據比例的性質就可以求出結果。
通過對比交流,引發學生深入思考,體會解決問題可以從兩個不同的方面建立比例關系,感受同一情境中“內在比”和“相間比”的兩種角度,發展比例推理能力。
學情調研及其分析應用在小學數學教學中具有重要作用。通過對“比例的應用”一課的解構,我們發現,每一個數學教學內容背后,總會有數學思想和方法在支撐。充分用好學情調研作品,找到激發學生思維的基點和生長點,并搭建思維進階的階梯,是進行高質量教學活動的有效途徑。
參考文獻:
[1]邵燕楠,黃燕寧.學情分析:教學研究的重要生長點[J].中國教育學刊,2013(2):60-63.
[2]徐夢杰,曹培英.精準針對學生差異的學情分析研究[J].課程·教材·教法,2016,36(6):62-67.
[3]LAMON S J. Ratio and proportion:connecting content and childrens thinking[J]. Journal for Research in Mathematics Education,1993,24(1):41-61.
[4]賴穎慧,尹稱心,陳英和.不同任務類型條件下4~6年級兒童比例推理策略的表現[J].心理發展與教育,2016,32(4):385-393.
[5]苗丹民.4~14歲兒童比例推理及認知結構的發展研究[J].心理學報,1991(2):167-177.
[6]李眾展.1~6年級學生比例推理的學習進階研究[D].杭州:杭州師范大學,2019:53.
(北京市海淀區中關村第三小學? ?100089)

