怎樣讓3的倍數特征的練習更有效
黃建


教師可以通過用數字卡片組數和推理,讓3的倍數特征的練習更有效。
一、組數——會判斷
【挑戰任務1】從1、2、3、4、5、6、7、8、9這九張數字卡片中選三張,組成能被3整除的三位數。
要求學生獨立完成后集體反饋。教師提問:“你寫的數能被3整除嗎?你是怎么判斷的?”引導學生利用能被3整除的數的特征進行判斷。
【挑戰任務2】用九張數字卡片組成三個三位數(每張數字卡片只能用一次),使這三個數都能被3整除,且三個數的和最小。
先讓學生獨立思考,再在四人小組內進行交流。預設學生發現要使得三個三位數的和最小,1、2、3可以放在百位,4、5、6可以放在十位,7、8、9可以放在個位。根據能被3整除的數的特征,得到多種結果:147、258、369或168、249、357或159、267、348。
二、爭辯——會說理
【挑戰任務3】A同學用2、0、6、7四張數字卡片,組成不同的四位數。對于這些數,三位同學有了這樣的判斷:佳佳認為“不可能是2的倍數”;迪迪認為“可能是5的倍數”;強強認為“一定是3的倍數”。你同意誰的說法?請說明理由。
讓學生獨立完成,同桌交流想法。教師反饋時引導:(1)佳佳說的錯在哪里?你可以舉一個反例嗎?(2)迪迪的說法有道理嗎?怎樣能把所有情況有順序地寫出來?(3)強強的想法是對的,不管這四張卡片怎么擺,各個數位上的數字的和都是2+0+6+7=15,15能被3整除,所以這些四位數都能被3整除。(4)繼續增加數字卡片,如果再給你一張,要讓組成的五位數能被3整除,那么你會怎么選?請說明理由。
三、論證——會推理
【挑戰任務4】有A、B兩堆數字卡片(如圖1)。請你從中選擇六張組成一個六位數,使得它能被3整除。說一說你是怎么想的?
先讓學生獨立完成,再在四人小組內進行交流。教師反饋時呈現學生作品(如圖2)。并提問:“這些數都是3的倍數嗎?你有什么發現?”
小結:只要是由六個5、六個7、三個5和三個7組成的數一定就是3的倍數。
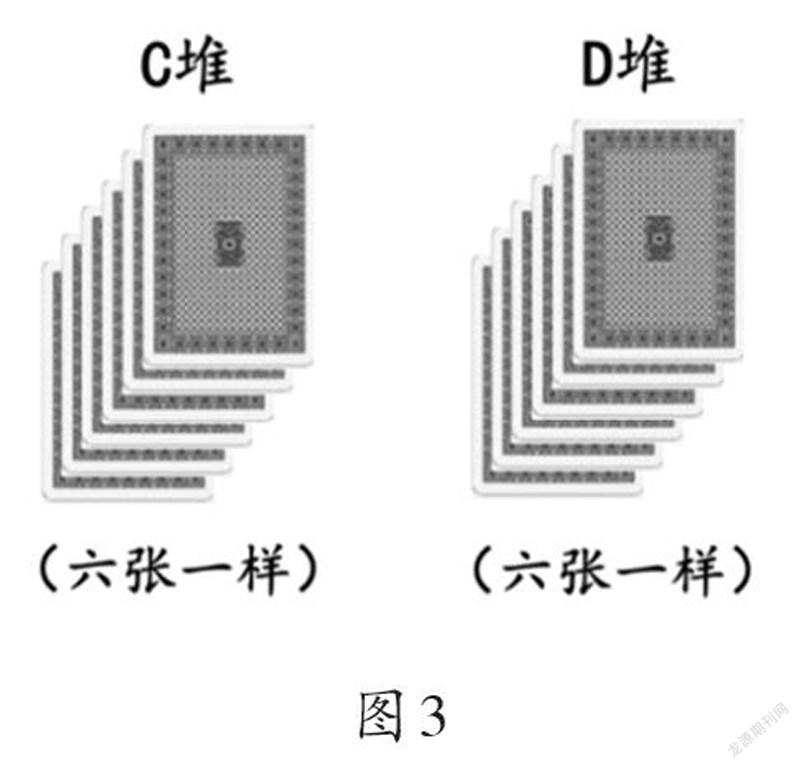
【挑戰任務5】有兩堆看不見數字的卡片C、D(如圖3),請你從中選擇六張組成一個六位數,使得它能被3整除。你會怎么選?
學生獨立思考,寫出自己的思考過程。全班反饋時,讓學生舉例說明。
小結:不管C和D是幾,由六張C、六張D、三張C和三張D組成的六位數一定都是3的倍數。
教師追問:為什么只要選三張C和三張D就一定是3的倍數?學生寫出思考過程后,教師出示學生作品(如圖4),并請學生說一說:你能看懂誰的想法?
以上過程,讓學生在組數中,有序思考,利用特征進行判斷;在爭辯中,綜合應用,打通數的特征;在論證中,理法結合,提升推理能力。
(浙江省杭州市勝利實驗學校? ?310008)

