武警院校學員評教指標體系分析與優化

摘 "要 "武警院校課堂教學質量評估體系主要涵蓋院、系督導組評價、教研室同行互評以及學員評教四個方面。其中，前三者通常采用上級訓練管理部門下發的評估指標，而學員評教指標體系由軍內各院校基于專業、生源、授課對象層次等因素自行構建與完善，具有一定的自主性。以大數據采樣為基礎，計算機軟件為工具，通過主成分分析優化其指標體系，合理分配各項指標權重，以期從學員視角客觀反饋教員的教學水平，提升其實戰化教學能力。

關鍵詞 "武警院校；教學質量；評教指標體系

中圖分類號：E251.3 " "文獻標識碼：B

文章編號：1671-489X（2022）11-0063-05

0 "引言

軍隊院校課堂教學質量評價指標體系及權重分配由上級制定，各院校可調整的余地相對較小。近年來，院校教育教學逐漸以學員為主體，學員評教受關注程度顯著上升。因各院校的培養對象存在差異性，評估指標和權重較難統一，且部分武警院校剛建立學員評教體系，各項指標尚未細化，故可在學員問卷調查、數據采樣的基礎上，分析指標的關聯性，進而采用主成分分析方法確定各指標權重，關注數據，排除主觀因素，充分發揮其評教功能，推動武警院校教學質量穩步提升。

1 "國內外研究教學評教體系基本情況

以習近平新時代強軍思想為指引，以各級常態化教學監測手段為抓手，指導軍隊院校開展課堂教學質量評估體系研究。目前，已有不少文獻從構建體系、優化指標、強化規則等方面進行調研及實踐。例如：解放軍理工大學的張強等[1]為解決部隊院校教學競賽評判規則問題，引入網絡層次分析法，并通過實例驗證該模型的有效性；空軍航空大學的李德軍等[2]立足軍校優質課建設，從建設思路、過程、方法和經驗等方面論證如何開展優質課，提高人才培養質量。

在評估體系研究方面，空軍一航院的陳迪等[3]就新形勢下課堂教學質量評價體系，提出構建多元、動態式的評價指標和網絡化信息評價系統，利于實時反饋督導信息；解放軍理工大學的胡友彬等[4]進一步倡導“教、學、管”三方聯動機制，構建動態人才培養質量跟蹤和評估體系，制定個性化人才培養細則，以期深化軍事高等教學體系改革；國防科技大學的李思等[5]就軍事工程類專業人才培養質量評估指標體系進行解讀，對一些難以量化的指標使用平均值量化法，可以一定程度避免主觀因素干擾。

此外，大數據背景下，部分地方高校在構建課堂教學質量評價指標體系方面的做法亦值得借鑒。例如：天津理工大學的景玉冰[6]探索涵蓋目標、過程、主體的全數據教學評價體系和框架設計，使其能反饋教師授課水平，為有關部門制定推進教學的措施提供參考依據；紹興文理學院的趙偉強等[7]以學生參與度、認可滿意度為核心指標，從大數據分析視角探索不同學科專業普適評價體系，尋求提高教學質量的有效途徑。

2 "基于主成分分析的權重計算基本思路

2.1 "基本原理簡介

首先確定當前學員評教指標體系之間的關聯程度，而后提取若干主成分，基于應用多元統計分

析[8]中成分矩陣（或稱載荷因子矩陣）和特征向量矩陣之間的關系，計算各指標在主成分表達式中的系數，再結合主成分的方差貢獻率（視為主成分的重要程度）加權平均得到相應指標系數，最后歸一化為指標權重。

2.2 "關鍵步驟

第一步：采樣，利用現有指標收集N個學員評教樣本（N＞100），并用極差法進行標準化處理。

第二步：借助SPSS軟件分析各項指標的內在關聯性，判斷能否提取主成分，并確定主成分的數量（一般選定指標變量協方差矩陣的特征值大于1的成分為主成分）。

第三步：確定所使用的綜合得分模型[8]，得分（score）=，，總分=

，，為指標系數。

第四步：對指標系數歸一化處理，得到各指標權重。

第五步：利用回歸分析方法驗證各項指標權重的合理性。

【注】Fj（j=1，…，m）為主成分（公因子，彼此之間內在關聯性較低）；為主成分的方差貢獻率（體現其重要程度）；Xk（k=1，…，p）為指標變量；λj為Xk（k=1，…，p）協方差矩陣的特征值（常稱為初始特征值）；akj為Fj與Xk的相關系數（），反映二者之間的相關程度。根據多元統計學[8]中描述的主成分性質，，即特征向量矩陣（主成分系數）=

成分矩陣，或稱載荷因子矩陣M=（akj）p*m。

該思路以標準化數據樣本為基礎，利用多元統計學知識[8]并結合數據分析軟件SPSS，提取各指標主要信息（累計方差貢獻率＞85%），分析得到各指標權重，一定程度排除了主觀賦權的情況，使各指標間的相對重要性得以體現。

3 "武警院校學員評教指標權重構建

基于權重計算基本思路，對武警院校學員評教指標體系進行重新賦權。當前學員評教體系主要采用四個一級指標，12個二級指標，指標體系如表1所示，進行評估。經過三輪試用，已累積500多條樣本信息。利用SPSS軟件分析各項指標之間的關聯程度，限于篇幅，僅給出六個二級指標的相關矩陣，如表2所示。

由軟件分析的相關性結果可知，上述指標體系之間存在一定程度的正（負）相關性。如節奏掌握與講課狀態相關系數為0.990，嚴格要求與批改輔導相關系數為0.897，說明上述變量間存在信息重復，考慮權重分配時需突出主要指標權重，適當降低次要指標權重值，因此需進一步利用主成分分析方法濃縮信息，確定主成分數量。

1）若選取選定初始特征值大于1的成分為主成分，則由SPSS軟件調用降維因子分析得到初始特征值大于1的三個主成分相應的成分矩陣和方差貢獻率，如表3、表4所示。

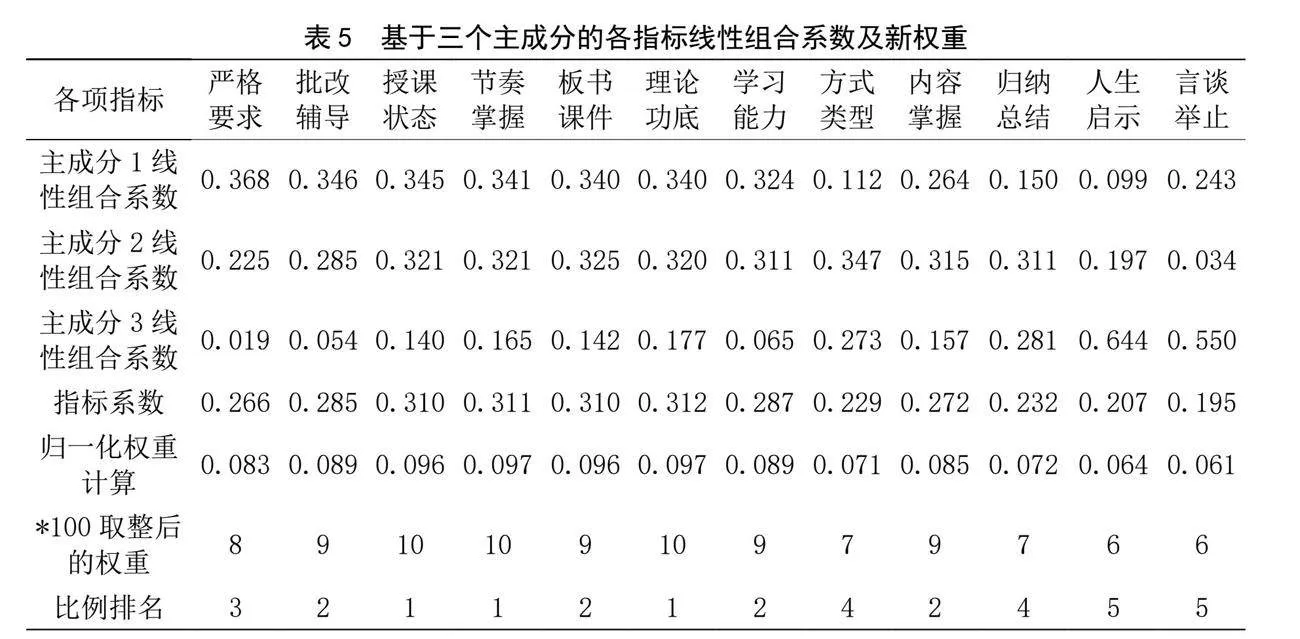
由表3可知，三個主成分的方差貢獻率合計為82.814%，即其攜帶的信息量超過70%，且特征值均大于1。故可進一步利用表3、表4的數據和前文關鍵步驟中的主成分線性組合系數計算方法得到前三項主成分的線性組合系數（即特征向量矩陣）和指標系數，最后歸一化處理即為各項指標的新權重，如表5所示。

利用線性回歸方程驗證此模型的合理性。將總分視為因變量，三個主成分視為自變量，調用SPSS軟件中的線性回歸程序，得到系數標化后的回歸方程：

總分估計值=0.264*主成分1+0.952*主成分2+

0.044*主成分3

再利用表5各成分的線性組合系數，得到以各二級指標為自變量的標準化線性回歸方程系數，如表6所示。回歸分析發現，表5各項指標權重的比例排名與表6回歸系數排名存在一定程度的差別，仍有進一步優化空間。

2）由表3可知前三個主成分攜帶的信息量不超過85%。第四個因子的特征值為0.669，雖小于1但大于0.6，若將其納入主成分，則方差合計貢獻率達88.39%，攜帶指標的大部分信息。故設定主成分數量為4，再次調用SPSS軟件的降維因子分析功能，得到其成分矩陣如表7所示。

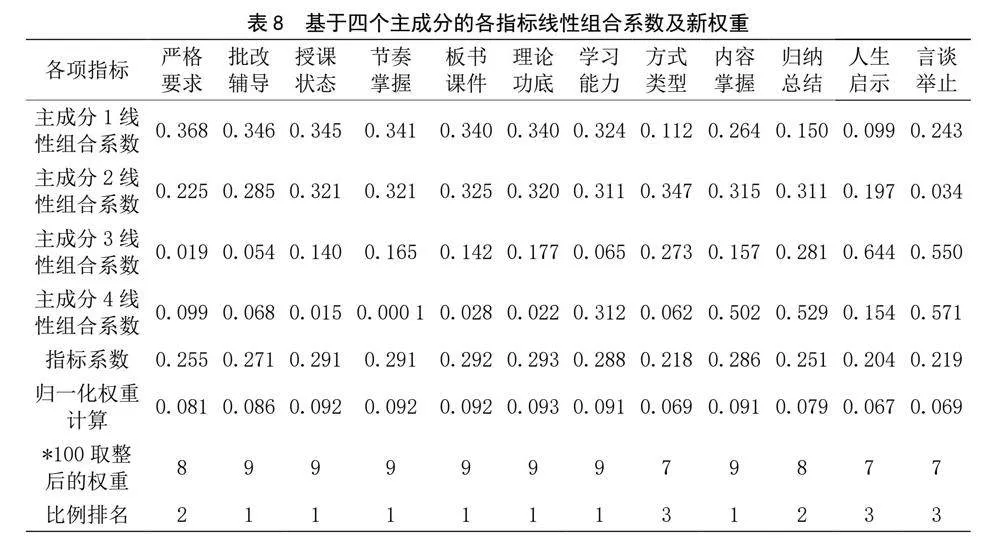
同上計算各主成分線性組合系數、指標系數，最后歸一化為新權重，如表8所示。

采用回歸分析方法驗證其合理性。調用SPSS軟件中的線性回歸程序，得到回歸方程：

總分估計值=0.950*主成分1+0.251*主成分2+

0.056*主成分3+0.095*主成分4

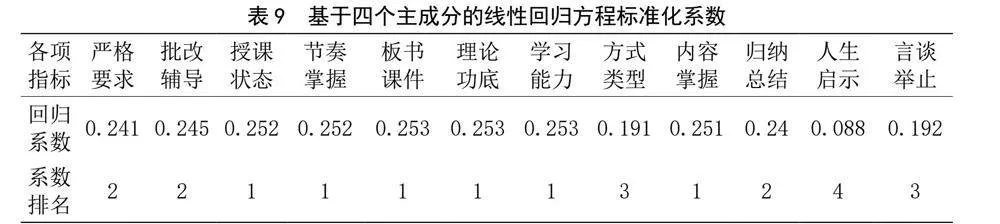
利用表8各成分的線性組合系數得到各指標為自變量的標準化線性回歸方程系數，如表9所示。

回歸分析發現，表8各項指標權重的比例排名與表9回歸系數排名較為一致，說明當主成分數量固定為4時，得到的指標權重比例較主成分數量為3時更為合理。進一步，基于表7中各主成分與指標之間的正（負）相關性，可重新劃分一級指標所屬范圍。

主成分1與嚴格要求、批改輔導成正相關，且成分矩陣系數均超過0.7，可以定義為教學投入及態度。

主成分2與授課狀態、節奏掌握、板書課件，理論功底、方法類型、學習能力、內容掌握成正相關，且成分矩陣系數均超過0.6，可以定義為教學綜合能力及反饋。

主成分3與人生啟示、言談舉止成正相關，且成分矩陣系數均超過0.6，可以命名為教姿教態及

影響；

主成分4僅與歸納總結成正相關，且成分矩陣系數超過0.4，可以定義為課堂教法與總結。

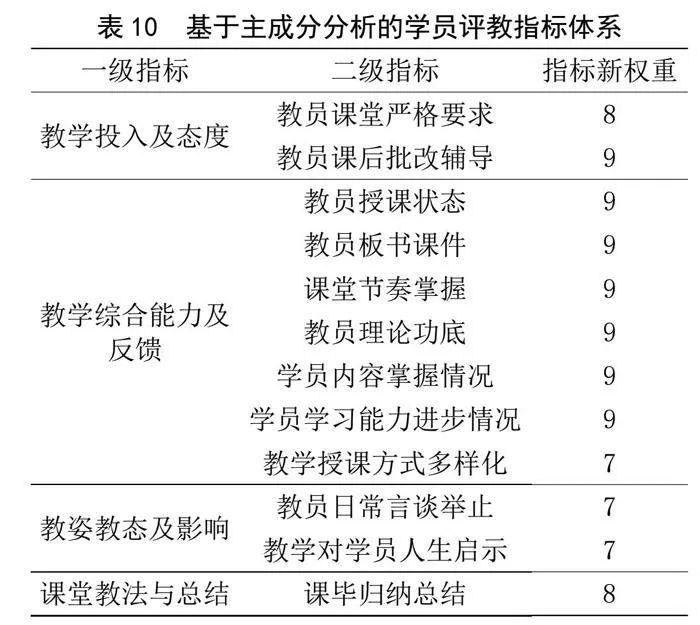
綜上所述，基于新的二級指標權重賦值和一級指標定義，得到學員新評教指標體系如表10所示。

分析指標體系，可得新指標體系中各項二級指標權重較為均衡，最大（小）權重值相差2。一級指標權重占比最大的是教員的教學綜合能力及反饋，占61%；次之是教員的教學投入及態度，占17%。二者從主成分分析角度客觀解釋學員對教員的能力、教學投入和自身掌握情況的重視程度。此外，由指標權重發現學員對教員的授課方法和課畢總結重視程度占15%，高于原體系。新體系對原體系的教學效果和教學態度這兩項一級指標進行重組，降低對應二級指標（教員日常言談舉止、教學對學員人生啟示）的權重（均降為7），客觀反映其比重。

4 "結束語

以學員日常評教數據為基礎，基于多元統計分析中的主成分分析原理及性質，利用數據分析軟件SPSS的相關功能，確定各項二級指標權重，并將主成分定為新的一級指標，從而重構學員評教指標體系。該體系從學員關注角度出發，一定程度反映了為戰育人、以學員為主體的教育思路。可以將此新學員評教指標體系應用于日常評教，并在實踐中不斷優化。

參考文獻

[1] 張強，張鵬，李長波.ANP-GRAP方法在軍校教學能力

競賽中的應用[J].計算機工程與應用，2015，51（12）：

260-263，270.

[2] 李德軍，趙文杰，郭峰.依托優質課程建設提高軍校

人才培養質量[J].長春教育學院學報，2015，31（9）：

100-101.

[3] 陳迪，候瑞娟.新形勢下軍隊院校課堂教學質量評價

體系改革研究[J].高教學刊，2016，2（14）：138-139.

[4] 胡友彬，張波，左瑞亭，等.軍校個性化人才培養機

制與評估體系探究[J].大學教育，2016，5（4）：51-52.

[5] 李思.軍校本科學員人才培養質量評估指標體系研究：

以某科技大學科學和工程技術類為例[J].教育教學

論壇，2018，9（15）：200-203.

[6] 景玉冰.高校全數據教學質量評價體系的研究與實踐

[J].天津商務職業學院學報，2014，2（2）：62-64.

[7] 趙偉強，陳坤，盧雪萍.基于大數據分析的教學評價

體系建立與實踐：以紹興文理學院為例[J].紹興文

理學院學報，2017，37（9）：111-117.

[8] 朱建平.應用多元統計分析[M].4版.北京：科學

出版社，2021：107-136.