隨機激勵下非線性能量阱系統減振性能優化研究

胡宏祥， 陳林聰,2

(1. 華僑大學 土木工程學院，福建 廈門 361021；2. 華僑大學 福建省智慧基礎設施與監測重點實驗室，福建 廈門 361021)

迄今為止，結構振動控制主要分為主動控制、半主動控制、被動控制、混合控制4種技術[1-2]。由其派生出的減振裝置各有特點，其中被動控制裝置以其設計制造簡單、成本低、無需外部供能等優勢成為減振首選方案。根據組成元件的特性差異，被動消能減振裝置又可分為線性和非線性兩種類別。線性裝置擁有眾多優勢，但其主要缺陷也不可忽略。一旦結構的特定模態頻率偏離線性裝置的固有頻率，或者環境激勵在其頻率帶寬之外，就會失去效果甚至會引起系統振動惡化。針對線性裝置的缺陷，非線性能量阱(nonlinear energy sinks，NESs)作為一類典型的具有非線性剛度的被動控制裝置，因其質量輕、頻率魯棒性強、能量耗散快等優點贏得了工程領域的關注。

當前，國內外關于NES的研究均有較多的成果，但主要集中于確定性載荷作用下的系統響應研究[3-12]，而實際結構往往承受著隨機激勵。針對耦合NES的隨機結構系統的研究尚處于起步階段。Starosvetsky等[13]采用蒙特卡洛直接模擬的辦法驗證了單自由度(single-degree-of-freedom，SDOF)系統與NES在窄帶隨機激勵下的減振效果。Xue等[14]利用隨機平均法與路徑積分法獲得了諧波和高斯白噪聲組合激勵下耦合NES單自由度系統的穩態響應。然而，直接采用隨機平均法，完全剔除了NES的影響。隨后，薛繼仁等[15]又直接采用數值方法求解FPK(Fokker Planck Kolmogorov)方程，獲得了高斯白噪聲激勵下耦合NES的單自由度系統穩態響應，討論了不同參數下系統的穩態響應特性。文獻[16]研究了窄帶隨機力作用下NES的振動抑制。引入變量將原系統轉化為等價系統，采用隨機平均法降低等效系統的維數，但采用Hermite級數法求解FPK方程可能會得到負的概率密度函數(probability density function，PDF)。

另一方面，學術界對NES的相關參數，包括質量比、初始條件和阻尼，特別是非線性剛度進行了很多優化研究以期獲得更好的減振性能。如，Shiroky等[17]提出了一種系統穩定性評估準則，用于估計NES的最佳阻尼值。Yang等[18]評估了NES參數對非線性系統傳輸速率的影響。劉良坤等[19]基于強調制反應的特性，得到NES剛度的最佳上下限。Vaurigaud等[20]通過對靶能量傳遞期間分岔現象的研究，提出了一種NES裝置的解析調諧方法，得到了簡諧激勵下NES的最優剛度。張也弛等[21]在忽略阻尼的保守系統的基礎上，利用近似慢變力學模型給出了完全能量傳遞的臨界質量比。可以看出，現有的工作都是屬于確定性激勵情形，但這些工作可為隨機激勵下耦合NES結構系統的參數優化問題提供重要的借鑒。

本文針對高斯白噪聲激勵下耦合NES單自由度結構隨機振動的參數優化問題，提出一種高效的數值方法。引入新變量，由原系統得到關于質心位移和相對位移的等價系統；應用加權殘值法，將等價系統等效為具有精確平穩解的隨機系統，再結合雅可比變換，導出原系統平穩響應概率密度函數的近似解析表達式；最后，以原系統平穩響應概率密度函數的近似解析解構造目標函數，以主結構位移與速度響應量的均方(mean-square，MS)最小為優化準則，確定不同控制條件下的NES最優參數以及變化規律，進而為實物設計提供可行性參考。

1 系統動力學模型

本文所考慮的力學模型由線性主結構和附在其上的NES裝置兩部分組成。主結構質量m1通過線性阻尼c1和線性剛度k1與地面相連。NES裝置由小質量塊m2, 三次非線性剛度k2和線性阻尼c2組成。該模型如圖1所示。

通過考慮動態平衡條件以及主體結構與NES之間的耦合作用，該系統的運動微分方程為

(1)

式中：X1和X2分別為主體結構和NES'相對于地面的位移響應；F(t)為作用于系統主結構的外部激勵。

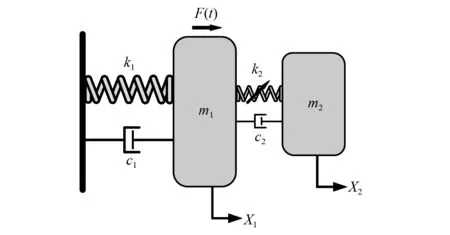
圖1 耦合NES的單自由度系統裝置Fig.1 A SDOF system coupled with NES device

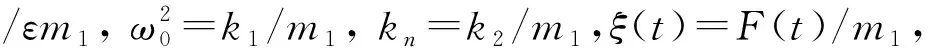
(2)

式中，ξ(t)為強度為2D的零均值高斯過程，滿足E[ξ(t)ξ(t+τ)]=2Dδ(τ),E(·)為數學期望，δ(τ)為Dirac delta函數。

現引入新變量

u1=X1+εX2,u2=X1-X2

(3)

式中，u1,u2分別為質心位移和相對位移。結合方程式(2),可得到關于u1與u2的等價系統。結果為

(4)

式中，Ci(i=1,2,…,6)具體表達式如下

(5)

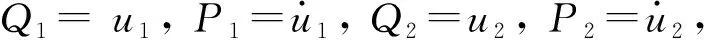
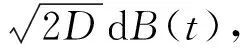
(6)

式中，B(t)為單位維納過程。

支配系統式(6)的穩態概率密度函數ρ的平穩FPK方程為

(7)

式中，mi(i=1,2,…,4)分別為

m1=p1,m2=-C1p1-C2q1-C3p2-C4q2,

(8)

方程式(7)的精確平穩解一般情況下無法獲得。另外，方程維數較高，直接數值求解所需的計算量和數據存儲量都較大，諸如有限差分法等數值方法不適合NES的參數優化分析研究。本文提出了一種基于原系統FPK方程與等效系統FPK方程的加權殘差最小化技術，求得原始系統平穩解的近似解析表達式，以達到NES參數優化分析的目的。

2 等效隨機系統

假設系統式(4)的等效系統如下

(9)

式中：Ci,eq(i=1,2,4,5,6)為待定系數；ξ1(t)和ξ2(t)為兩個強度均為D，零均值的獨立高斯白噪聲。

與式(9)對應的平穩FPK方程為

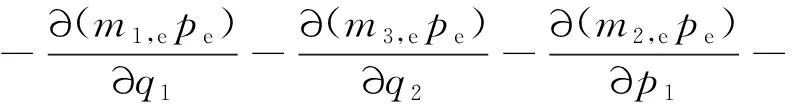
(10)

式中：ρe為等效系統的平穩概率密度函數；mi,e(i=1,2,…,4)分別為

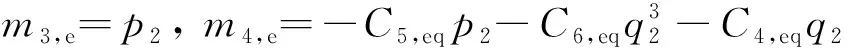
(11)

平穩FPK方程式(10)具有精確平穩解，其表達式為

(12)

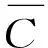
利用ρe取代式(7)中的ρ，得到誤差δ

(13)

比較式(13)與式(10)，可進一步得如下表達式

(14)

其中

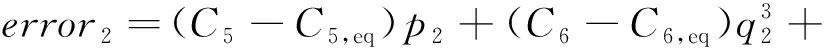
(15)

將加權多項式函數應用于式(14)，并將殘差均方在整個域上進行積分，即

(16)

式中，ρf為忽略高階累積量的截斷方法得到的原系統的聯合平穩概率密度函數。式(16)中的加權函數建議取如下的多項式形式[22]

總之，小學語文教學中培養學生綜合閱讀能力是新課標的主要要求。在實際語文教學中，需要教師引導學生進行詞句基礎訓練、教導學生正確閱讀的方法及引導學生深入感悟文章的內涵，以讓學生掌握文章整體脈絡，從而提高學生的綜合閱讀能力。

(17)

式中，Kij通常取1。

等效系統中的未知系數由最小均方誤差準則確定，即

?E(Δ)/?Cj,eq=0,j=1,…,5

(18)

式中，E(·)為數學期望。

求解方程組式(18)，即可得到未知系數Ci,eq。將結果代入式(12)，得到等效系統的平穩解。在系統參數ε=0.05,λ1=0.1,λ2=0.1,kn=0.5,ω0=1.0,D=0.01(0.005)時不同激勵強度下等價系統式(4)的邊緣概率密度響應，如圖2所示。圖2中：實線為蒙特卡洛模擬(Monte Carlo solution，MCS)的結果；符號為本文方法得到的數值結果，可知理論解和蒙特卡洛模擬解在誤差允許范圍內吻合，表明文中提出的數值方法有效。

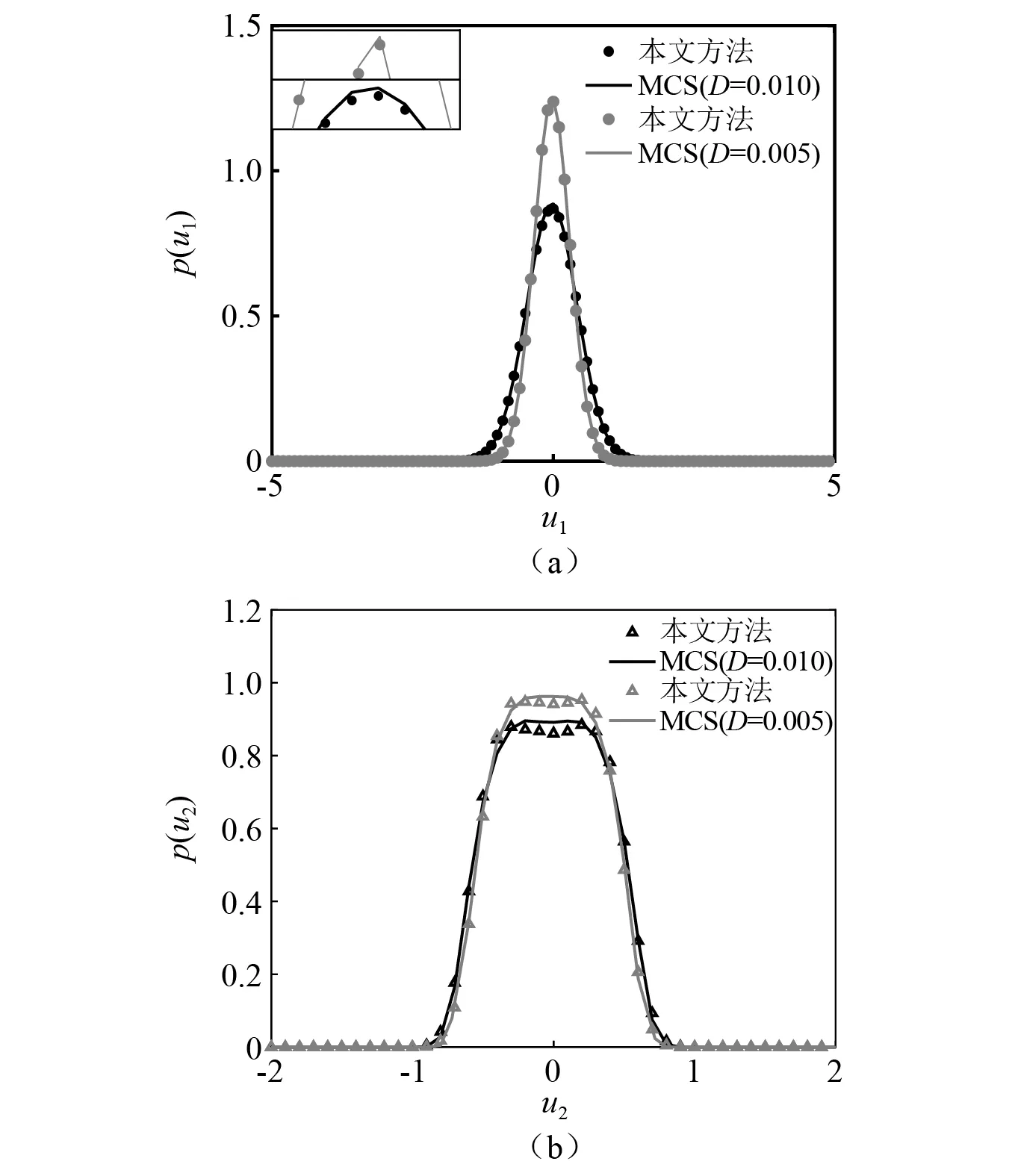
圖2 不同激勵強度時等價系統式(4)的邊緣概率密度Fig.2 Themarginal PDF of equivalent system

在獲得方程式(12)基礎上，利用雅可比矩陣進一步獲得原始系統穩態概率密度函數的近似表達式，即

(19)

式中，|J|為與式(3)相關的雅可比行列式。鑒于概率密度函數ρ完全描述了隨機變量Xi(t)(i=1,2)響應的統計特性，并且具有解析的表達式，可為開展NES參數優化設計提供必要的條件。

3 NES的參數優化分析

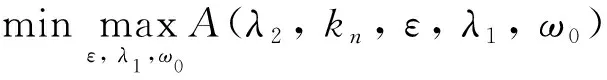
(20)

式中：Gi(i=1,2)分別為阻尼系數λ2和剛度系數kn的取值范圍；λ2,kn,ε為設計變量；A(ε,ω0,λ1,λ2,kn)為NES減振效果的性能指標。請注意，式(20)中的問題無法用常規方法直接分析計算。但是，通過選取合適的目標函數，就能夠把問題轉化為一般的非線性優化問題，即

minσ(λ2,kn,ε,λ1,ω0)
subject to.λ2∈G1;kn∈G2

(21)

式中，σ為參數優化的目標函數。本文以主結構位移與速度響應量的均方為目標函數，NES控制參數的優化設計采用直接搜索法。算法流程如圖3所示，所采用的優化步長和參數空間，如表1所示。

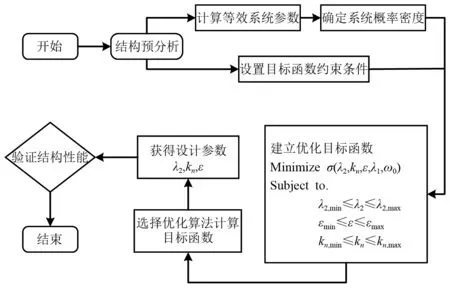
圖3 參數優化流程圖Fig.3 Flow chart for parameter optimization

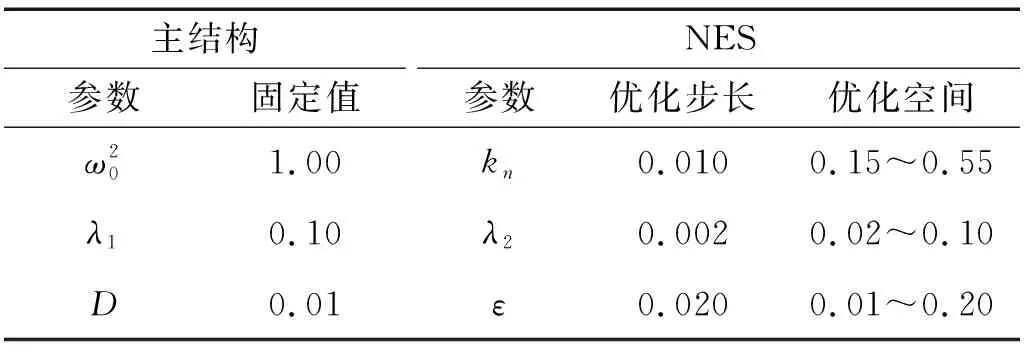
表1 NES參數優化條件Tab.1 Parameters of optimization condition

本節考察了阻尼系數λ2，剛度系數kn和質量比ε對NES減振性能的影響規律。不同質量比ε= 0.01,0.05和0.10時關于主結構位移與速度均方隨λ2與kn的變化規律，如圖4～圖6所示。由圖4～圖6可知，關于位移均方和速度均方的變化趨勢基本一致。λ2的增加能有效地降低主結構響應，即NES的減振性能隨λ2的增加而提高。在給定的范圍內，最佳值位于給定區間的邊界處。增加質量比ε可以顯著降低系統的均方響應值,即NES的減振性能會得到有效提高。針對非線性剛度值kn對NES的減振性能影響規律與質量比的取值相關。當質量比較小時，參見圖4和圖5，主結構均方響應隨著非線性剛度值kn的增加，先減小后增加，即存在一個使均方響應保持在最低水平的最優非線性剛度區間。然而，當質量比取0.1時，見圖6，主結構均方響應的變化規律與質量比較小情形存在明顯差異，隨著非線性剛度值kn的增加，主結構均方響應先增加達到一個最大峰值，隨后開始衰減。因此，在質量比取較大值時，非線性剛度值kn的設計需謹慎，有可能加劇系統振動，降低NES的減振性能。

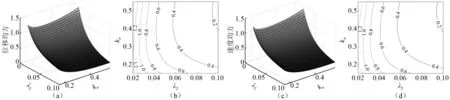
圖4 當ε=0.01時主結構的位移與速度均方隨λ2與kn的變化規律Fig.4 The change regularity of MS of displacement and velocity with λ2 and kn for ε=0.01

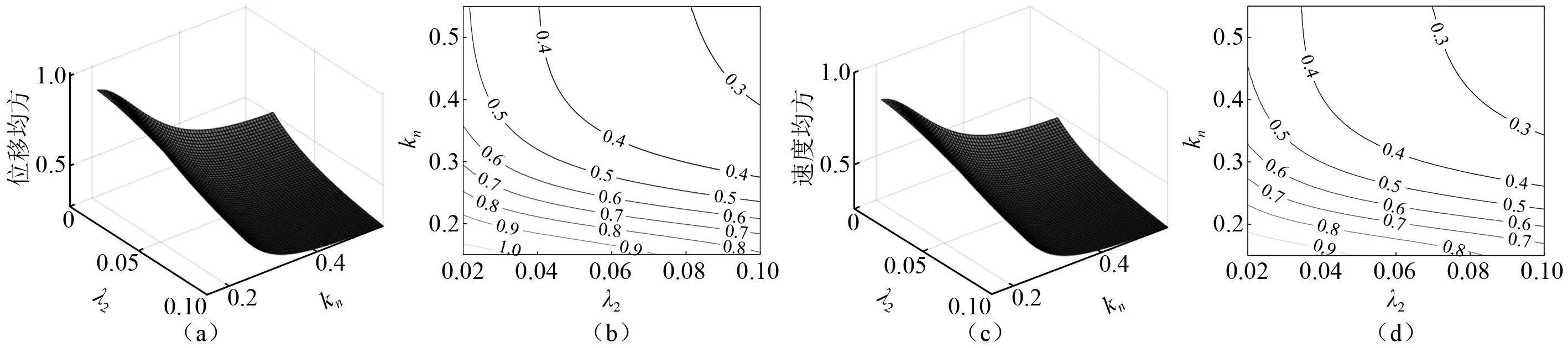
圖5 當ε=0.05時主結構的位移與速度均方隨λ2與kn的變化規律Fig.5 The change regularity of MS of displacement and velocity with λ2 and kn for ε=0.01

圖6 當ε=0.1時主結構的位移與速度均方隨λ2與kn的變化規律Fig.6 The change regularity of MS of displacement and velocity with λ2 and kn for ε=0.01

在最優參數NES、偏離參數優化值NES以及未控情形時(未耦合NES)系統主結構位移的瞬態與穩態響應概率密度函數的蒙特卡洛模擬結果，如圖7所示。圖7中：X1為主結構的位移響應；ρ(X1)為對應位移的概率密度。與無NES情形相比，處于最優NES參數與偏離優化值的NES參數情形下系統響應的概率密度顯著降低，即兩者均可有效地降低系統的響應，同時包括瞬態與穩態響應，但優化參數下的NES效果更為顯著，也進一步表明本文提出的設計方法對于穩態與瞬態響應均有較好的效果。

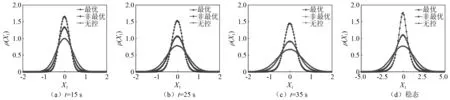
圖7 不同時刻主結構位移響應概率密度函數的蒙特卡洛模擬結果Fig.7 The PDF of displacement of main structure at different time obtained with Monte Carlo simulation

4 結 論

本文針對高斯白噪聲激勵下耦合NES單自由度結構隨機振動的參數優化問題提出了一種高效數值方法。應用加權殘值法，將原系統等效為具有精確平穩解的隨機動力學系統。理論解和蒙特卡洛模擬解在誤差允許范圍內吻合，顯示所提的數值方法有效。在此基礎上，利用原系統的平穩響應概率密度函數的近似解來構造主結構位移與速度響應量均方的目標函數，進行NES減振性能參數優化設計。綜合分析了隨機激勵下NES的最優參數及其變化規律，得出以下主要結論：

(1) 在典型的高斯白噪聲隨機激勵下，耦合NES結構的動力響應顯著降低，表明NES能夠有效實現結構振動控制的性能目標。通過選擇有效結構參數能在較大程度上提高NES的減振性能。

(2) 參數研究表明，質量比ε與阻尼系數λ2的增大能有效提高NES的減振性能。非線性剛度kn在質量比較小時存在最優剛度區間，當質量比取到較大值時，kn的增大可能會引起系統振動惡化。

(3) 基于結構性能的NES參數設計方法，以主體結構位移和速度響應量的均方最小為優化目標，來衡量NES減振性能。在充分發揮NES在結構振動控制方面優勢的同時，又能滿足目標性能的要求。

(4) 本文所涉及的NES并不是唯一形式，根據不同的應用需求，各類型NES的振動控制有待深入研究。