軸向力作用下過屈曲Timoshenko梁與Euler-Bernoulli梁的自由振動特性對比

井 潔， 毛曉曄， 丁 虎， 陳立群

(上海大學 力學與工程科學學院 上海市應用數學和力學研究所，上海 200444)

在道路交通、橋梁建筑、工程機械等領域，梁是普遍使用的結構。在已有經典梁理論中，Euler-Bernoulli梁理論忽略了橫向剪力和切應變的影響，適用于細長結構。但是，這種簡化會高估梁的彎曲剛度，因此，Timoshenko梁理論被提出來以研究短粗結構。即使是細長梁，在考慮高階振動時，剪切變形的影響依然是不可忽略的，因此Timoshenko梁理論相比Euler-Bernoulli梁理論具有更高的精確性，尤其是對于動力學而言[1]。

在實際應用中，梁往往會承受軸向應力，這會對梁的動力學特性產生較大影響。許醇義[2]通過數值計算推證軸向力對彎曲振動自振頻率的影響，發現各種支承梁由于承受軸向壓力使剛度減小，頻率隨壓力的增大而減小；杜紹洪[3]通過有限差分法求解了簡支梁的橫向自由振動問題，構造出求解四階非穩態線性偏微分方程的差分隱格式，數值試驗表明構造的隱格式絕對穩定并且具有很高的精度階。Ma等[4]研究了軸力作用下多裂紋梁的模態及疲勞壽命分析，發現軸向力除了會改變梁的動力學特性，還會加速梁的疲勞破壞； Karimi等[5]研究了梁在隨機軸力作用下的非線性振動分析，結果表明梁的平均和均方值都是時間的函數，這意味著梁的側向位移是一個非平穩過程； Li等[6]系統地研究軸向受壓Timoshenko梁的彎曲、屈曲和自由振動問題，在模型中引入了表征變形過程中軸力方向的過渡參數，結果表明，過渡參數對軸向加載梁的彎曲、屈曲和自由振動均有顯著影響，頻率隨軸向壓力的增大而減小，這對軸力方向的確定具有重要意義； Liu等[7]研究了非連續梁在不同軸向載荷和連接彈簧剛度作用下的撓度和振動頻率，結果表明，隨著連接彈簧剛度的增大，連接彈簧的撓度呈指數級減小，振動頻率呈指數級增加。這些研究都表明，軸向力的存在會對梁的動力學特性及使役性能產生重要影響。

當軸向壓力繼續增加，一階固有頻率會減小至零，結構發生過屈曲現象[8]，梁會變成本質非線性結構，其動力學響應會產生更復雜現象，例如在低頻區域產生超諧波共振[9]。因此，研究梁承受過軸向力導致的過屈曲是很有必要的。諸多學者已經對不同結構的屈曲現象進行了研究，比如李世榮等[10]研究了加熱彈性梁在熱過屈曲構形附近的自由振動，數值結果表明，梁在未屈曲時，各階頻率都隨升溫而單調下降。在過屈曲后則相反；Li等[11]采用Timoshenko梁理論和高階剪切變形梁理論對柱形結構穩定性進行了研究，重點分析了Engesser’s和Haringx’s假設對屈曲的影響。結果表明，兩種假設對強剪切剛度柱的屈曲載荷影響不大，而對弱剪切剛度柱的屈曲載荷影響顯著。平動彈簧剛度對屈曲載荷的影響比轉動彈簧剛度更明顯。Ziane等[12]考察了矩形空心截面的簡支鋼梁，考慮到較大的扭轉和截面畸變，利用同倫攝動法研究了后屈曲非線性路徑，得到了外力偶引起橫向扭轉屈曲臨界值的閉合表達式。Einafshar等[13]針對薄壁梁的軸向彎曲屈曲、后屈曲和幾何非線性分析，提出了一種高效的一維有限元模型。為驗證模型的有效性，進行了各種屈曲、后屈曲和非線性彎曲試驗，證明了所提薄壁梁穩定性和幾何非線性分析公式的有效性和準確性。Ferreira等[14]研究復合材料蜂窩梁的屈曲和后屈曲分析，隨著腹板長度的增加，腹板屈曲模式由局部屈曲變為后屈曲。這種效應增加了臨界整體剪切。因此，相比非屈曲結構，屈曲結構的動力學研究更具挑戰，目前還在不斷發展完善。

對于梁結構，常用Timoshenko梁模型及Euler-Bernoulli梁模型。滕兆春等[15]基于Euler-Bernoulli梁建模，研究了過屈曲軸力下的橫向自由振動。各階頻率在過屈曲前隨軸向壓力的升高而單調下降，這是由于軸向壓力的存在使梁的撓度增加，相當于減少了梁的剛度，使固有頻率降低，過屈曲附近一、二階頻率隨軸向壓力的升高而單調增加。而劉吉源等[16]利用瑞雷法得到任意邊界條件下的Timoshenko梁固有頻率泛函方程，對兩邊均為固定端約束的情形建立了頻率方程，并分別討論了軸向力、轉動慣量和剪切變形對頻率方程解的影響，進而得到相應的固有頻率。Ding等[17]首次發現了轉動慣量和剪切變形對超臨界軸向運動梁橫向振動的影響；王樂等[18]從Timoshenko梁平衡方程出發，建立了軸力作用下Timoshenko梁自由振動偏微分方程，給出了求解Timoshenko梁固有頻率的方程，探究了其橫向振動特性，計算結果表明軸向壓力對最低階頻率的影響最大，階次越高影響越小。Khodabakhsh等[19]采用非線性Timoshenko梁模型對功能梯度材料柔性輸流管道的后屈曲和非線性振動進行了分析研究。數值結果證明了在分析短粗功能梯度材料管道時考慮截面旋轉慣性和剪切變形的重要性，特別是對于初始振幅較高的剛性材料，再次說明將Timoshenko梁模型用于短粗梁研究的必要性。以上這些研究都肯定了Timoshenko梁模型在描述短粗結構的精確性，但是，對于其在過屈曲軸力作用下，其共振頻率如何變化，特別是在基本過屈曲構形附近各階頻率如何變化，目前還缺少定量的研究結果。

本文基于Timoshenko梁建模，討論了在軸力過屈曲時梁的自由特性，并且與Euler-Bernoulli梁進行了對比分析。應用廣義哈密頓原理建立控制方程[20]，用Galerkin法離散成多自由度系統。在過屈曲狀態下，得到了梁的固有頻率，并討論了參數影響。

1 數學模型對比

圓形截面梁如圖1所示，材料密度為ρ，長度為L，橫截面直徑為D，兩端受簡支支撐。圖1中：x和y分別為軸向和徑向坐標；v(x,t)為梁的橫向位移；t為時間。截面繞中性軸的轉動慣量為I，剪切模量為G，楊氏模量為E，泊松比為μ，且受軸向力P作用，參數值如表1所示。

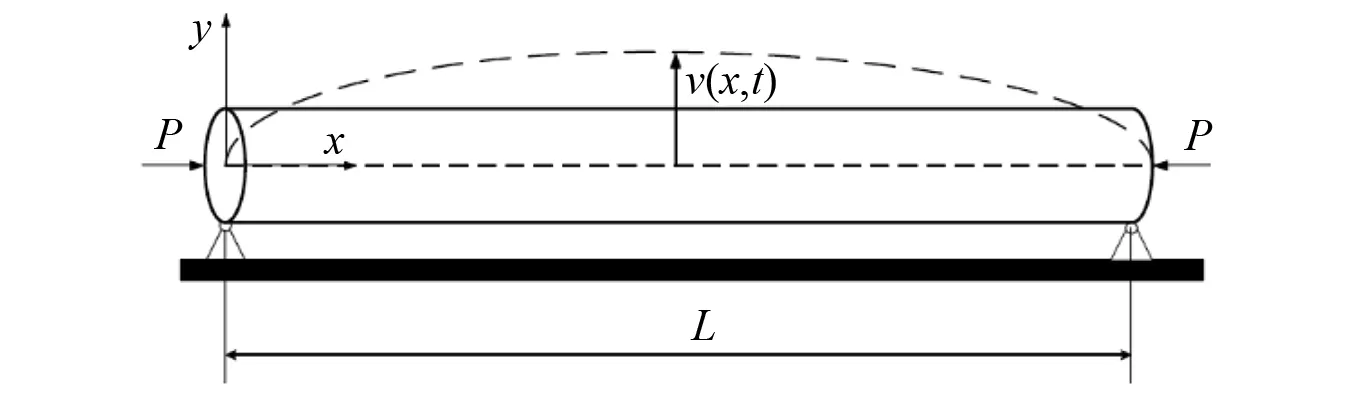
圖1 梁的物理模型Fig.1 Physical model of the beam

表1 梁物理參數Tab.1 Physical parameters of the beam

1.1 Timoshenko梁模型控制方程

對于短粗梁，參考Tan等[21]的控制方程建立過程，采用Timoshenko梁模型進行建模基于廣義Hamilton原理，導出Timoshenko梁橫向振動偏微分-積分控制方程

(1)

式中：A為梁的橫截面積；v(x,t)為梁的橫向位移；x或t前面的逗號為對x或t的偏導數；ks為圓形截面剪切修正因子,其表達式為

(2)

根據表1中泊松比的取值，將其代入式(2)，ks則可取為0.89。

兩端簡支邊界條件為

(3)

1.2 Euler-Bernoulli梁模型控制方程

同樣，參考Tan等研究中應用Euler-Bernoulli梁理論建立控制方程的過程，可推導得到Euler-Bernoulli梁橫向振動控制方程

(4)

簡支邊界條件如下

(5)

對比控制方程式(1)和式(4)可以看出Timoshenko梁模型為二階偏微分方程組，而Euler-Bernoulli梁模型則為四階偏微分方程。因此，Timoshenko梁在橫向和轉角兩個廣義坐標上分別具有兩個邊值條件，而Euler-Bernoulli梁僅在橫向廣義坐標上具有4個邊值條件。

2 過軸向力靜態屈曲分岔對比

2.1 簡支梁屈曲非平凡位形解析解

考慮屈曲失穩引起的屈曲非平凡位形，由于其與時間坐標無關，忽略方程式(1)中的時間項，得到靜態控制方程

(6)

兩端簡支邊界條件為

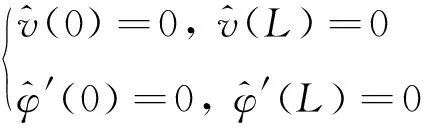
(7)

通過式(6)和式(7)，得到Timoshenko梁屈曲非平凡位形解析解

(8)

同理可以得到Euler-Bernoulli梁的屈曲非平凡位形解析解

(9)

式中，k為任意非零整數，在此將k取為1，研究第一階屈曲非平凡位形。

兩種梁模型的第一階屈曲非平凡位形對比圖，如圖2所示。由于屈曲非平凡位形關于零平衡位形軸對稱，因此本文只考慮正屈曲非平凡位形。圖2中：實線表示Timoshenko梁的橫向位形和轉角；點線表示Euler-Bernoulli梁的橫向位形；Pcr為梁的臨界軸向力。圖2選取的過屈曲軸向力為臨界軸向力的1.1倍。從圖2可知，Euler-Bernoulli梁的橫向位形大于Timoshenko梁。

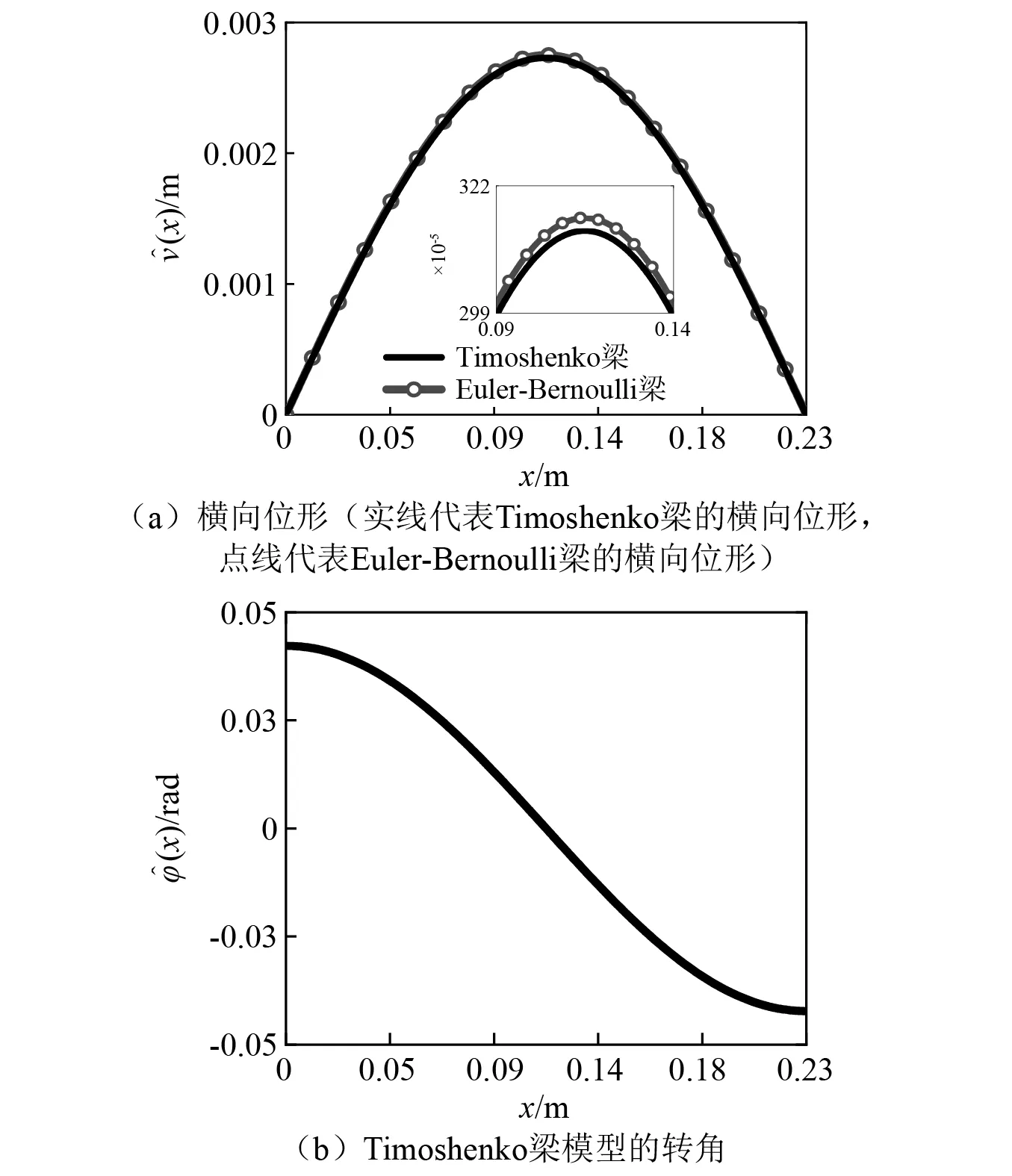
圖2 兩種梁模型的屈曲非平凡位形(P=1.1Pcr)Fig.2 The buckling non-trivial configuration of two beam models (P=1.1Pcr)

2.2 簡支梁屈曲非平凡位形穩定性

考慮第一階屈曲非平凡位形，不考慮外激勵及阻尼，從截斷方程中得到第一階截斷方程，最終得到第一階非平凡位形上的未擾系統

(10)

其中

(11)

將該方程改寫為狀態方程，提取自治系統Jacobian矩陣，當矩陣特征值λ存在正實部時，一階位形不穩定。與Euler梁一階位形的穩定性對比，如圖3所示。當軸向力達到屈曲值后，兩種模型的一階位形都穩定，但臨界軸向力存在差異，顯然Timoshenko模型因為考慮了截面轉動，剛度稍弱于Euler-Bernoulli模型，臨界屈曲發生地更早。

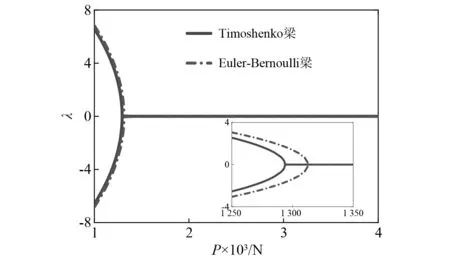
圖3 一階屈曲非平凡位形的穩定性Fig.3 Stability of first-order buckling non-trivial configuration

高階屈曲非平凡位形與Euler-Bernoulli模型一致，都不具有穩定性。

2.3 參數對軸向力靜態屈曲的影響

兩種梁模型的臨界軸向力可以通過式(8)和式(9)得出

(12)

為了更清晰地描述兩種模型之間的差異，定義了臨界軸向力的相對誤差

(13)

式中：Pcr-E為Euler-Bernoulli梁模型的臨界軸向力；Pcr-T為Timoshenko梁模型的臨界軸向力；RPL為兩種梁模型臨界軸向力隨長度變化的相對誤差，同理RPD為兩種梁模型臨界軸向力隨梁截面直徑變化的相對誤差。梁越細長，臨界軸向力越小，且Euler-Bernoulli梁因剛度大于Timoshenko梁，其臨界軸向力總是大于Timoshenko梁，如圖4(a)所示。隨著梁長的增加，這種差異越來越小，說明細長結構可采用Euler-Bernoulli梁理論。由圖4(a)可知，在梁長大于0.1 m時，兩種梁模型臨界軸向力隨長度變化的相對誤差小于10%，而在圖4(b)所取的范圍內，臨界軸向力隨梁截面直徑變化的相對誤差總是小于1.5%，說明兩種梁臨界軸向力對長度變化的敏感程度大于對截面直徑的敏感度。

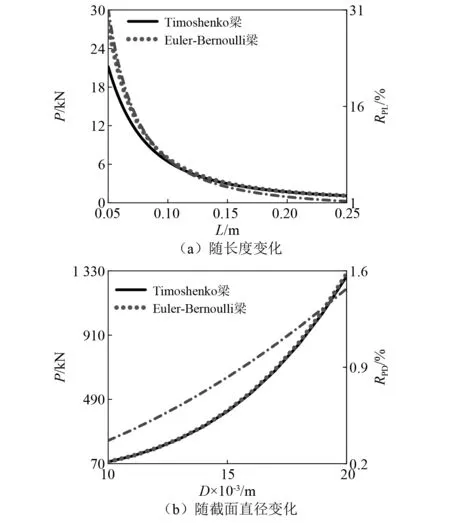
圖4 兩種梁模型臨界軸向力的比較及相對誤差Fig.4 Comparison of critical axial forces and relative errors for two beam models

兩種梁模型的中點位移和軸向力之間的關系，如圖5所示。由圖5可知，引起Timoshenko梁平衡分岔的軸向力要小于Euler-Bernoulli梁的軸向力。但Timoshenko梁的平衡變形要大于Euler-Bernoulli梁的平衡變形。此外，當梁較短或較厚時，兩種梁模型之間的差異更明顯。

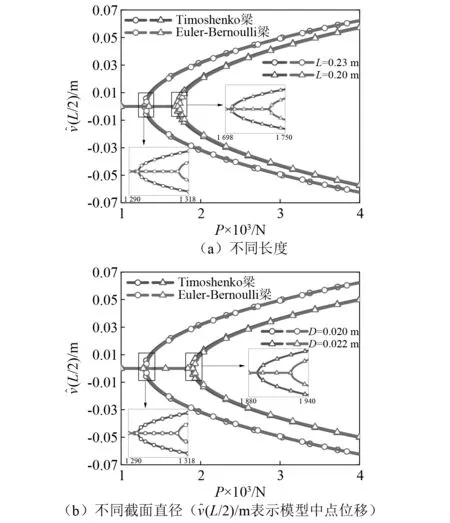
圖5 兩種梁模型隨軸向力的變化情況Fig.5 Variation of two beam models changing with axial force

3 過軸向力固有頻率對比

3.1 Galerkin截斷

對于過軸向力下的簡支Timoshenko梁，由式(1)推導得到自由振動控制方程

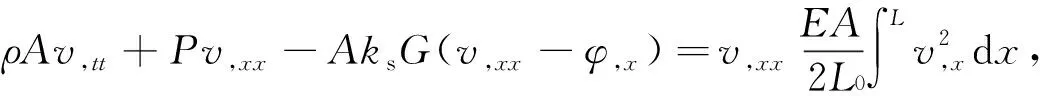
(14)

對式(14)進行坐標代換

(15)

(16)

式(16)存在非線性項，對其進行局部線性化，得到

(17)

設式(17)的解為如下形式，僅保留前m階

(18)

(19)

設權函數為模態函數自身，采用Galerkin法，得到離散的常微分方程系統。基于該離散系統，即可求解屈曲后Timoshenko梁的自由振動固有頻率。系統剛度矩陣可寫為如下形式：式(20)為屈曲前的剛度矩陣，式(21)為屈曲后的剛度矩陣

(20)

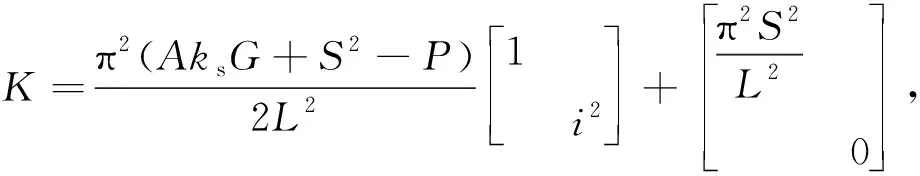
(21)

從式(20)和式(21)可以看出，在屈曲前，高階頻率會受到軸力的影響，而在過屈曲發生后，高階剛度矩陣分量中不含軸力項，所以高階頻率不隨軸力變化。

Galerkin截斷得到的，隨軸向力變化的前兩階固有頻率，如圖6所示。由圖6中可知，在屈曲發生前，隨著軸向力的增加，前兩階固有頻率都在減小。但是在屈曲后，隨著軸向力的增大，一階固有頻率隨之增大，而二階頻率不發生變化。

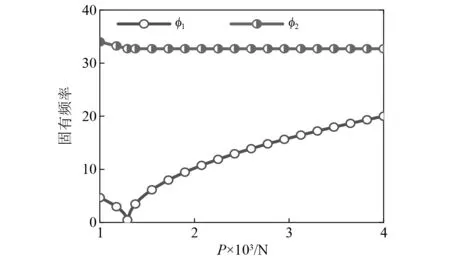
圖6 Timoshenko梁的前二階頻率Fig.6 The first-two order frequencies of the Timoshenko beam

此外，基于線性派生系統式(17)，得到了嚴格意義上的模態，因此截斷后廣義坐標解耦，模態坐標間不存在能量交換，截斷階數不影響結果的收斂性。因此在接下來的文章中，如無特別說明，都將采用二階Galerkin截斷法對控制方程進行截斷降維處理。

3.2 固有頻率對比

為了便于展示出兩種梁模型的差異，定義前兩階固有頻率的相對偏差

(22)

式中：fEi為Euler-Bernoulli梁模型的第i個固有頻率；fTi為Timoshenko梁模型的第i個固有頻率；Ri為固有頻率的誤差率。由圖7可知，相同參數條件下，兩種梁的前兩階固有頻率隨軸向力的變化趨勢定性相同：屈曲前都隨軸向力減小；而在屈曲后，一階頻率隨軸向力的增大呈增大趨勢，二階頻率基本不受軸向力的影響。但在定量上，兩者存在區別：由于Timoshenko梁屈曲更早，相同的過軸向力下，其一階頻率大于Euler梁一階頻率。因二階頻率不受過軸向力影響，其二階頻率一直比Euler梁小，且差異要大于一階頻率。

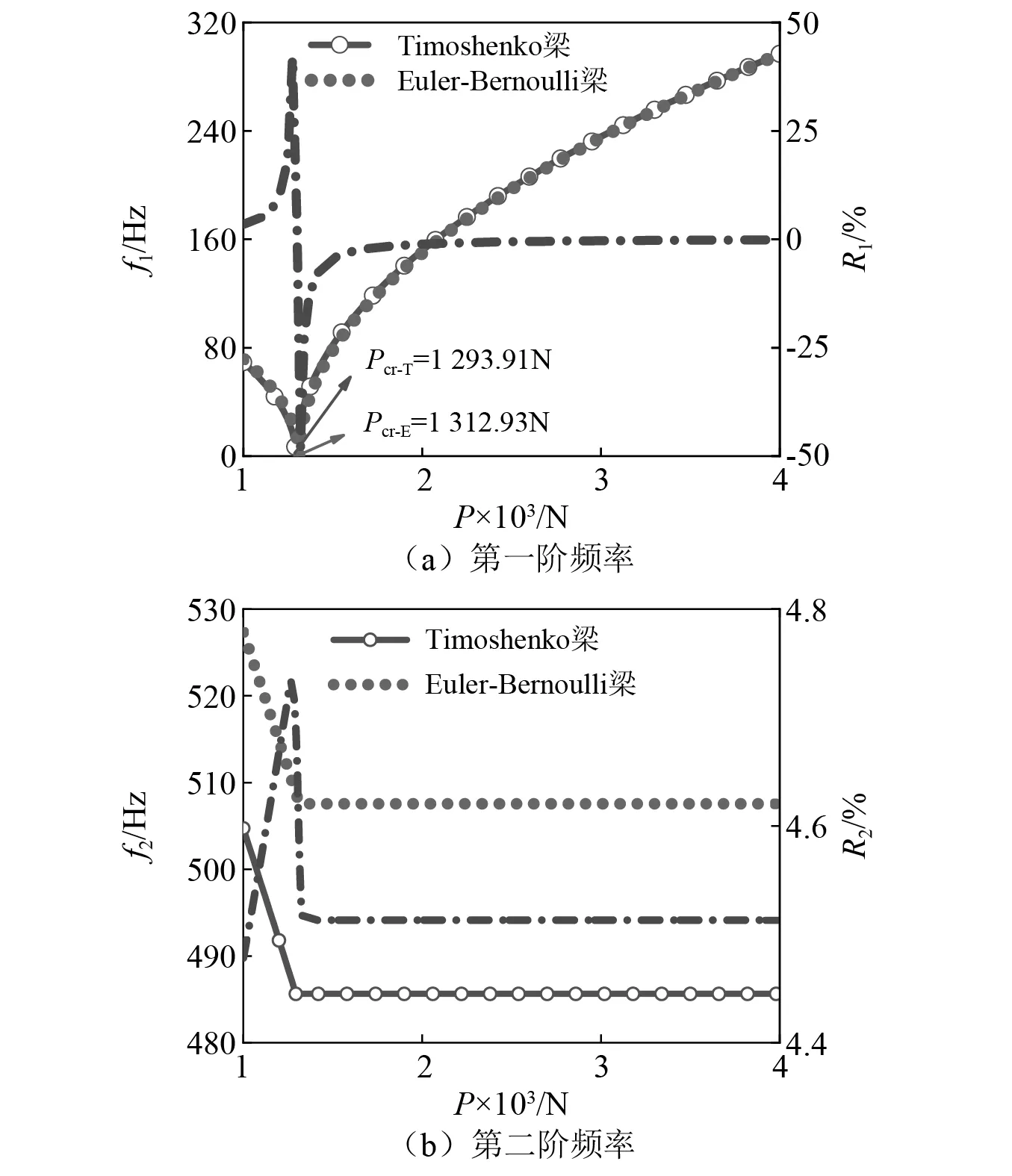
圖7 兩種梁的前二階頻率對比Fig.7 Comparison of the first-two order frequencies of the two beams

3.3 參數對固有頻率的影響

與2.3節一致，不同梁長和截面直徑條件下，Timoshenko模型和Euler-Bernoulli模型前二階頻率隨過屈曲軸向力的變化，分別如圖8、圖9所示。見圖8(a)和圖9(a)，隨著梁長的增加，一階頻率差異減小。雖然圖示兩種梁長的頻率存在交叉現象，但將橫坐標分別做對應臨界軸向力的移軸后，依然是較短的梁比較長的梁具有更高的固有頻率。見圖8(b)和圖9(b)，兩種梁模型的第二階固有頻率不隨軸向力變化，但Euler-Bernoulli梁的二階頻率總是大于Timoshenko梁的二階頻率。

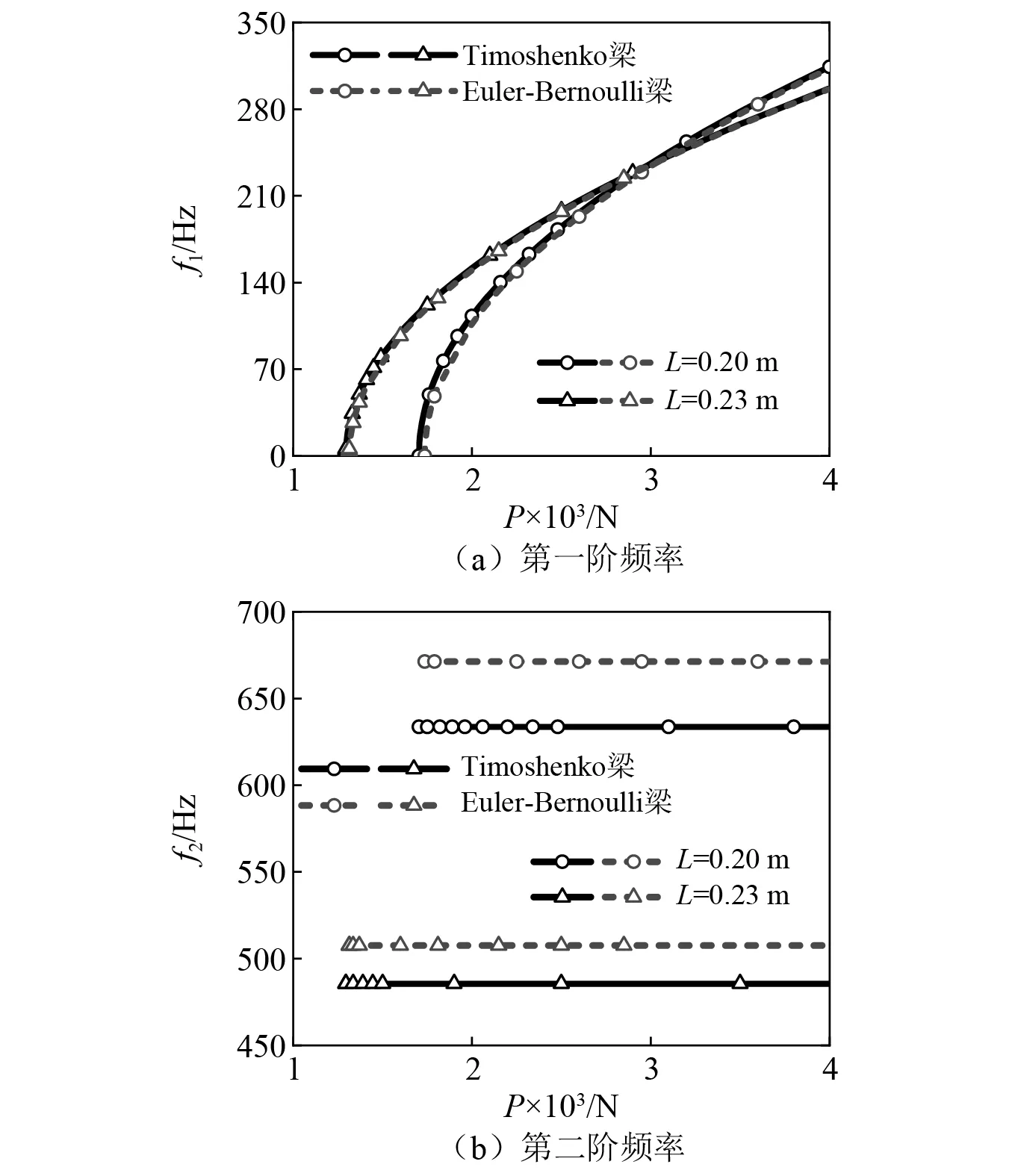
圖8 長度不同時兩種模型的固有頻率對比Fig.8 Comparison of the natural frequencies of the two models with different lengths

同樣選取2.3節的參數條件，長細比對固有頻率相對誤差的影響，如圖10所示。圖10(a)清楚地表明，隨著軸力的增加，兩種模型第一階過軸力屈曲固有頻率的相對偏差呈現出減小的趨勢，兩種模型越來越接近。在軸力大于3 000 N時，第一階固有頻率的相對誤差小于1.5%。在同一軸力條件下，長細比越大，固有頻率的差值越小。由圖10(b)可知，同一長細比條件下，第二階固有頻率的誤差不受軸力影響，長細比越大，兩種模型第二階固有頻率的相對誤差越小。

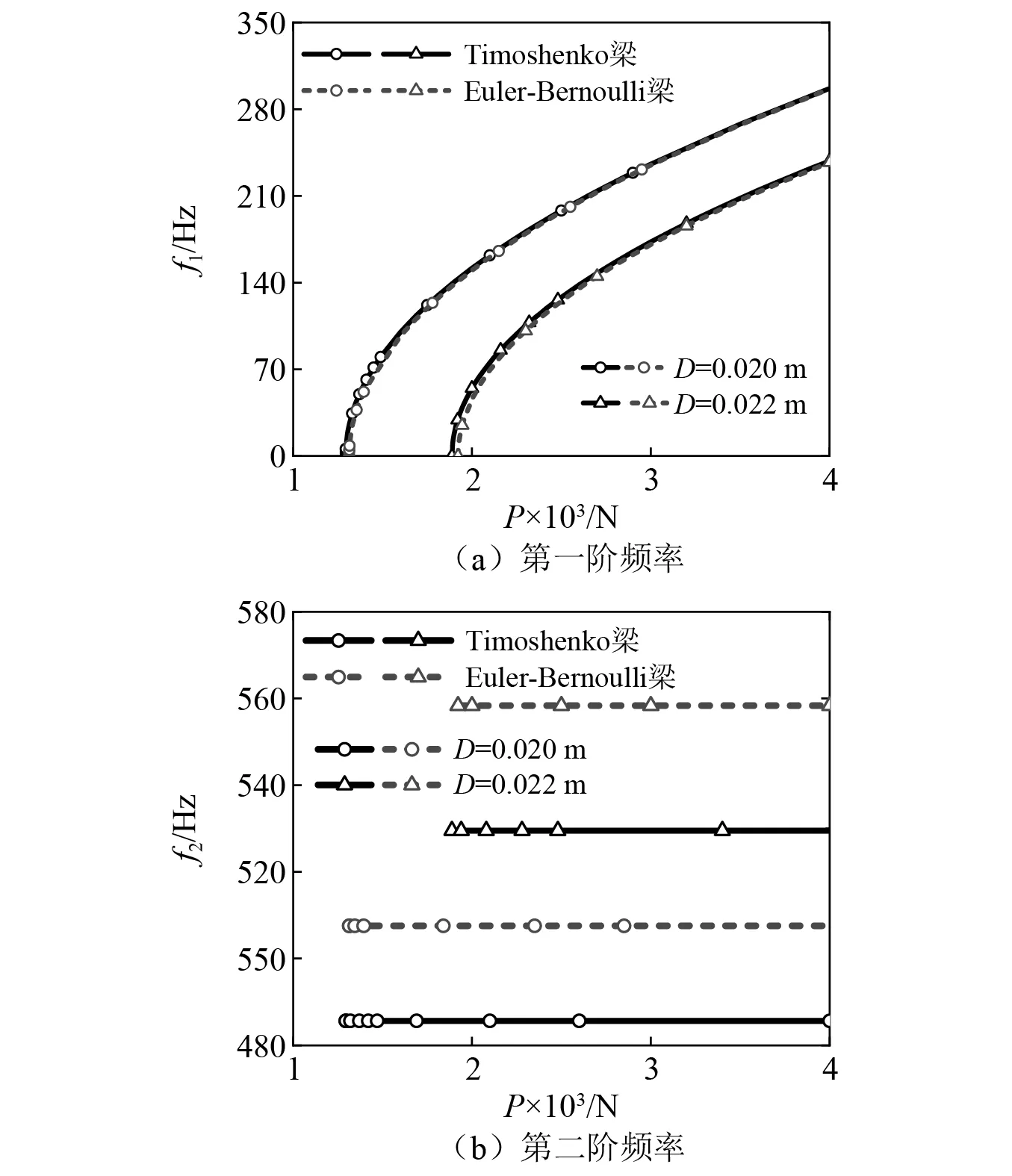
圖9 截面直徑不同時兩種模型的固有頻率對比Fig.9 Comparison of natural frequencies of two models with different section diameters

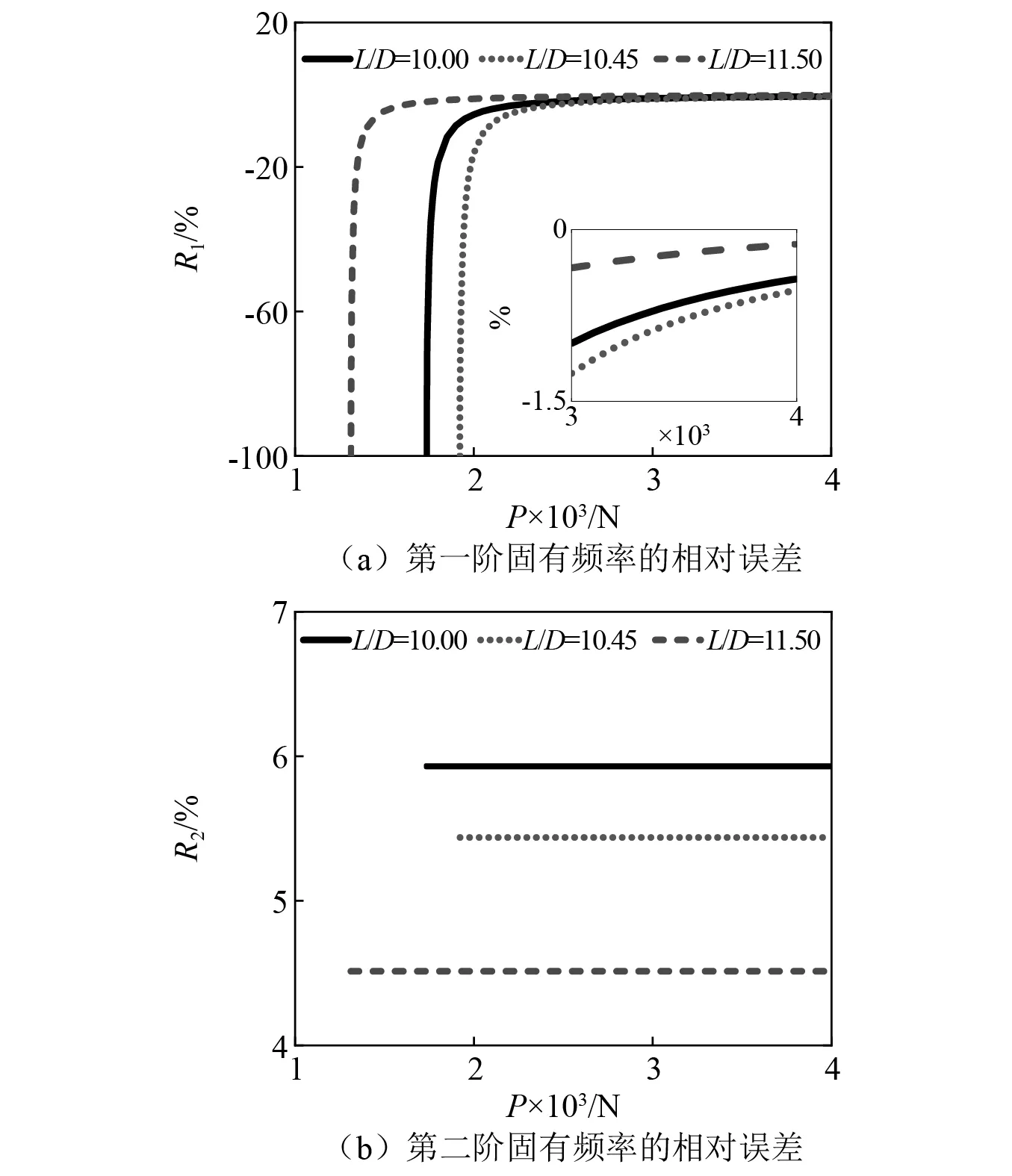
圖10 兩種模型在不同長細比下前兩階固有頻率的相對誤差Fig.10 The relative error of the first two natural frequencies of the two models under different slenderness ratios

為詳細探討截面轉動對Timoshenko梁剛度的影響，在此分析了不同橫向變形下的彎曲勢能和剪切勢能。在2.1節中已經推導出了簡支梁屈曲非平凡位形解析解，如式(8)所示。可見每一個軸力都對應一個屈曲位形，所以在此變為研究不同軸力下的彎曲勢能和剪切勢能，其表達式為

Ub=?VσxεxdV,Us=?VτyxγyxdV

(23)

式中：V為梁的體積；Ub和Us分別為Timoshenko梁的彎曲勢能和剪切勢能；σx和εx分別為法向應力和法向應變；τyx和γyx為剪切應力和剪切應變。梁的彈性本構關系為

σx=Eεx,τyx=ksGγyx

(24)

應變-位移關系為

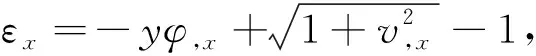
(25)

式中，y為橫截面上任意點距中性面的距離。以上均可參考Tan等研究中的建模過程。

由圖11可知，彎曲勢能和剪切勢能隨軸力的增大均呈增大趨勢。但不同的是，彎曲勢能是非線性增大，而剪切勢能是線性增大。所以剪切勢能占總變形勢能的比重隨軸力的增大而減小，截面轉動軟化了Timoshenko梁的剛度。即軸力越大，剪切勢能占比越小，彎曲勢能占比越大，兩種模型越接近。這一結論也可以與“圖10(a)清楚地表明，隨著軸力的增加，兩種模型第一階過軸力屈曲固有頻率的相對偏差呈現出減小的趨勢，兩種模型越來越接近”相互驗證。

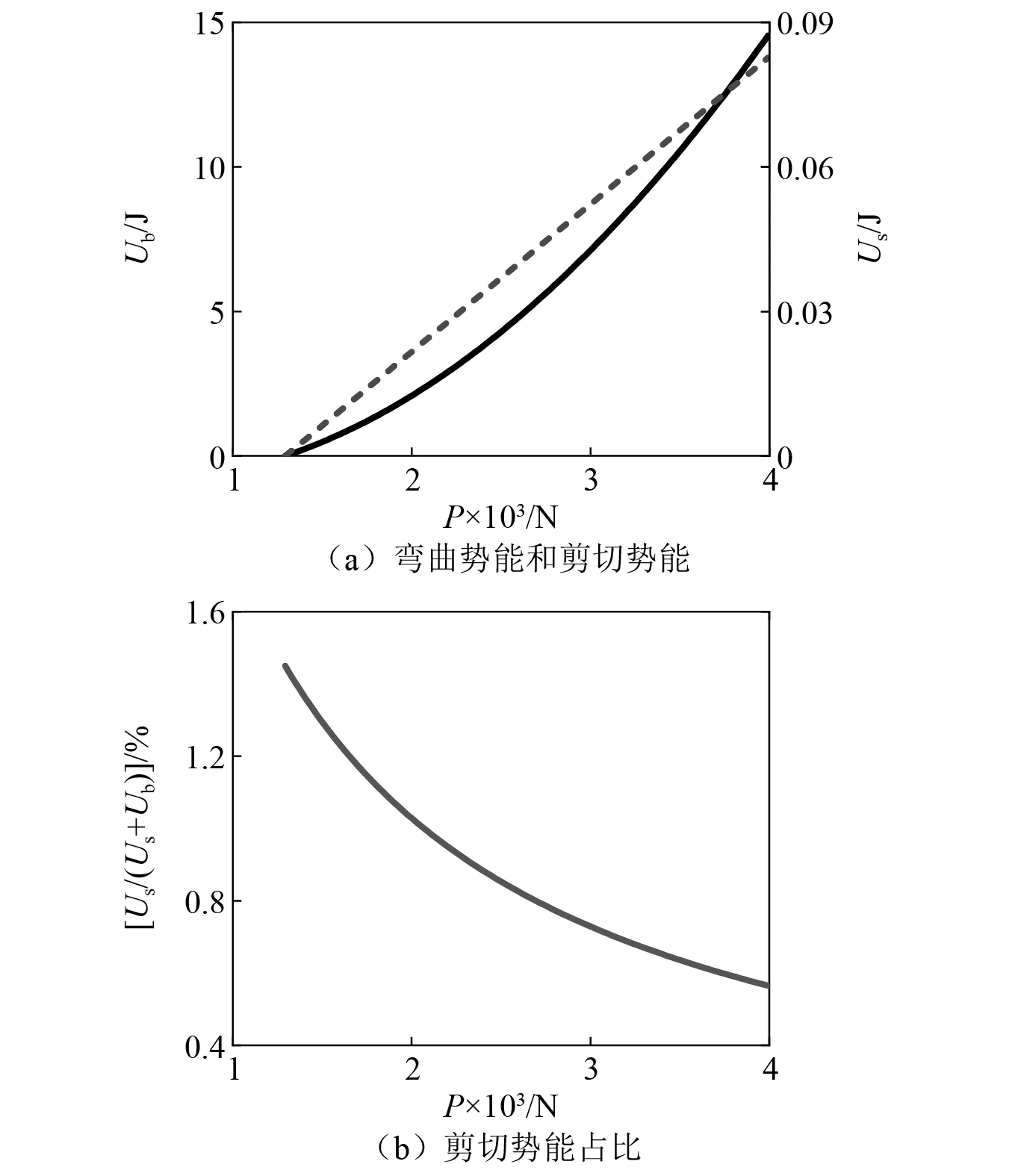
圖11 不同軸力下的勢能及占比圖Fig.11 Potential energy and its proportion under different axial forces

4 結 論

本文研究了軸向力過屈曲的條件下，Timoshenko梁的振動特征，并與Euler梁模型進行對比分析。通過Timoshenko梁模型，建立兩端簡支條件下屈曲壓力、屈曲后位形的解析表達式，并判斷一階位形的穩定性。運用Galerkin截斷法計算了梁在軸向力過屈曲條件下的固有頻率，確定系統參數的影響，并且對彎曲勢能和剪切勢能進行分析討論，得出如下結論：

(1) 與屈曲前固有頻率與軸向力的關系相反，在過屈曲發生后，一階頻率隨軸向力的增大而增大，二階及二階以上頻率不隨軸向力變化。

(2) 兩種梁臨界軸向力對長度變化的敏感程度大于對截面直徑的敏感度。且Euler-Bernoulli梁過屈曲軸向力比Timoshenko梁大，即Timoshenko梁比Euler-Bernoulli梁更早進入過屈曲狀態。

(3) 在屈曲前，Euler-Bernoulli梁的固有頻率總是大于Timoshenko梁；在屈曲后，由于臨界屈曲發生更早，Timoshenko梁的基頻在相同軸向力下總是大于Euler-Bernoulli梁；但將過屈曲軸向力與兩種模型相應臨界軸向力做歸一化處理后，Timoshenko梁基頻仍然大于Euler-Bernoulli梁。

(4) 軸力越大，兩種梁模型一階頻率相對偏差越小，Timoshenko梁的剪切勢能所占比重越小，兩種模型越接近。由此可以看出，Timoshenko梁的一部分振動能量存儲在截面轉動變形中，軟化了彎曲剛度，這種軟化作用在高階頻率上體現更明顯，與Euler-Bernoulli梁相比，高階頻率差異要大于基頻。

(5) 對于長細比較大的梁，固有頻率差值會越小。進一步說明了將Euler-Bernoulli梁用于細長梁研究、而將Timoshenko梁用于短粗梁研究的合理性。