機器學習算法在濟南泉群水位流量預測中的應用

于詢鵬，仇東山，曹美

（1.濟南市水文中心，山東 濟南 250014；2.濟南眾聯電子科技有限公司，山東 濟南 250100）

濟南城區泉水噴涌點主要包含趵突泉泉群、黑虎泉泉群、五龍潭泉群、珍珠泉泉群四大泉群，泉水可持續噴涌是濟南作為旅游城市以及生態文明城市建設重要的體現。濟南市水文中心自2010 年承擔濟南市四大泉群水位流量監測任務，目前已積累了大量的泉水監測數據。文章利用機器學習方法對四大泉群水位流量進行回歸分析，并評價分析多種算法對回歸數據的可靠性和準確性，以得出最優的回歸方程式，便于進行泉群出水量的預測。

目前機器學習算法主要包括有監督學習、無監督學習。前者主要應用在分類和回歸任務，后者主要應用在聚類任務，針對泉群地下水位和流量回歸分析屬于典型的有監督學習。目前，傳統的水文流量推算是根據實測水位流量數據進行簡單的曲線擬合，但擬合精度較差，通過機器學習可極大提高擬合精度和效率。本文分別通過機器學習的線性回歸、梯度下降、嶺回歸、水文模型等算法對歷史樣本數據進行分析，并比較各算法預測成果的優劣。

數據分析平臺采用Python 編程語言，開發環境采用Anaconda Jupyter notebook，機器算法使用Scikit-learn（sklearn）、Numpy 和Pandas 等分析庫，圖形庫選用Seaborn、matplotlib。

1 四大泉群水位流量樣本采集與分析

1.1 樣本采集

自2010 年開始進行四大泉群的流量監測，所有樣本數據選用2010—2021 年12 年的監測數據，實測水位流量數據期間的趵突泉地下水位選用濟南城鄉水務局趵突泉地下水位觀測井遙測數據，樣本數據采集曲線見圖1、圖2。

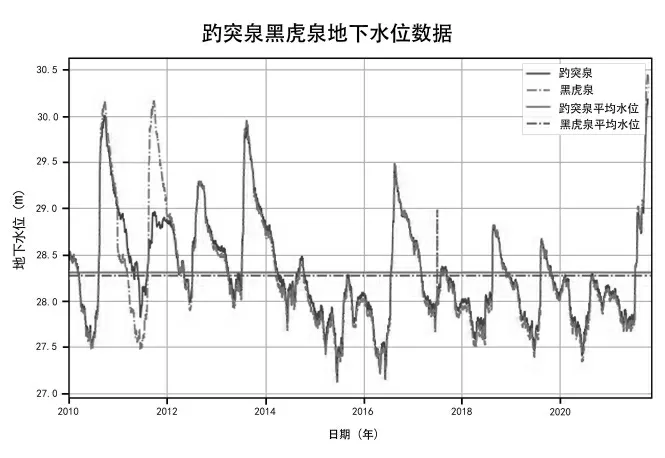
圖1 趵突泉、黑虎泉地下水位數據

圖2 趵突泉地下水位與泉群日流量實測數據

由圖1、圖2 可知，水位數據分別在高中低水位都有分布，樣本數據選擇合理，實測流量數據與趵突泉地下水位呈明顯的線性分布。本次趵突泉、黑虎泉地下水位數據樣本量4 320個，實測流量數據樣本量544個，趵突泉地下水位分布區間27.16～30.18 m，平均水位28.30 m，黑虎泉地下水位分布區間27.12～30.46 m，平均水位28.27 m，四大泉群總出水流量數據分布區間0.14～4.59 m3/s，日出水量分別為1.24～39.6 萬m3，平均日出水量16.3 萬m3。

1.2 相關性分析

從實測數據樣本中分別選取趵突泉地下水位和泉群總出水流量作為相關性分析變量，使用Seaborn 庫中的API 函數regplot 進行相關分析，見圖3。

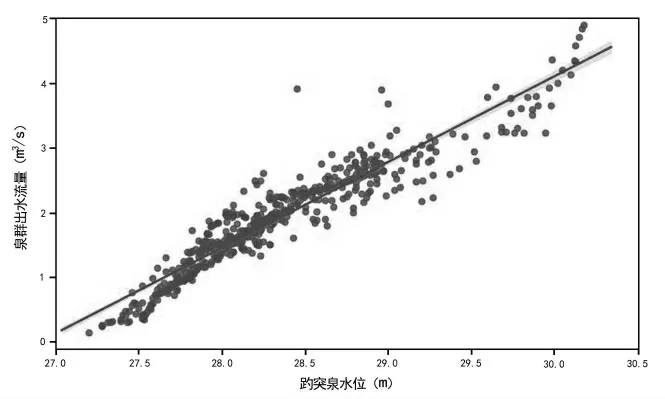
圖3 趵突泉水位與泉群出水流量實測數據

通過計算可知，趵突泉水位與泉群流量相關系數為0.952 6，趵突泉水位與黑虎泉水位相關系數為0.966 8。從樣本數據散點圖和相關性計算結果可以看出趵突泉地下水位與泉群流量以及趵突泉與黑虎泉具有高度正相關性，兩者的相關系數分別達到0.95 和0.96 以上，可以進行回歸預測分析。

2 趵突泉水位和泉群流量線性回歸分析

2.1 數據清洗和整理

整合自2010 年7 月至2021 年10 月之間所有的實測數據，根據實測日期讀取相同日期對應的趵突泉地下水位，分別計算每個測次泉群各個出水斷面出水流量，合計為四大泉群總出水流量，個別缺測斷面數據使用相同水位下的實測值填充，樣本數據整合結果見表1。

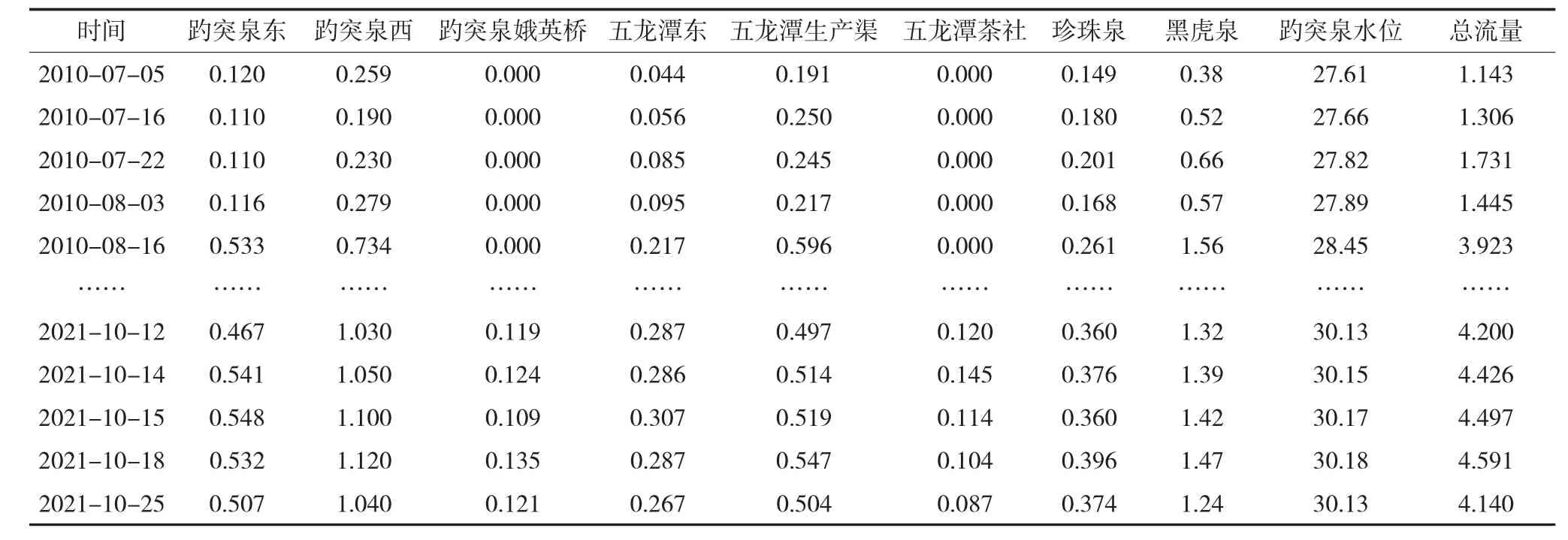
表1 樣本數據整合結果表 m3/s

2.2 回歸分析及預測成果評價

假設趵突泉地下水位與泉群總出水流量的線性方程為y=β0+β1x+ε，其中x 為因變量趵突泉水位，y 為自變量泉群總流量，β0為截距，β1為權重系數，ε 為誤差項，實測樣本數據利用最小二乘法擬合期望值，使每個實測流量點到擬合直線的離差平方和最小，并通過推導求出β0、β1的估計值，方程式如下：

分別從sklearn 庫中導入回歸分析所用的函數庫，并使用sklearn 庫中的函數對擬合直線進行MSE（均方差）、R-square（確定系數）的計算，以確實各種回歸模型的優劣，本數據分析使用以下sklearn 庫。

1）劃分訓練集及測試集：from sklearn.model_selection import train_test_split。

2）數據歸一化處理：from sklearn.preprocessing import StandardScaler。

3）線性正規方程：from sklearn.linear_model import LinearRegressio。

4）嶺回歸：from sklearn.linear_model import Ridge。

5）梯度下降：from sklearn.linear_model import SGDRegressor。

此外，通過把資料整編率定的水文模型lnQ=0.167+1.015 ln（ΔZ）納入到評估體系中，其中ΔZ為因變量，是泉群斷流趵突泉水位線的高程差，初步確定為26.7 m。把實測流量樣本數據分割為訓練集和測試集，其中測試集分割為總樣本數的20%，分別把測試集數據代入到各個回歸模型中，并返回回歸方程，把測試集數據導入模型預測函數，并生成預測值，最后，把預測值與實測值進行平均誤差、MSE（均方差）、R2（確定系數）計算，來評估各個回歸模型的擬合效果。各回歸模型預測評估結果見表2。

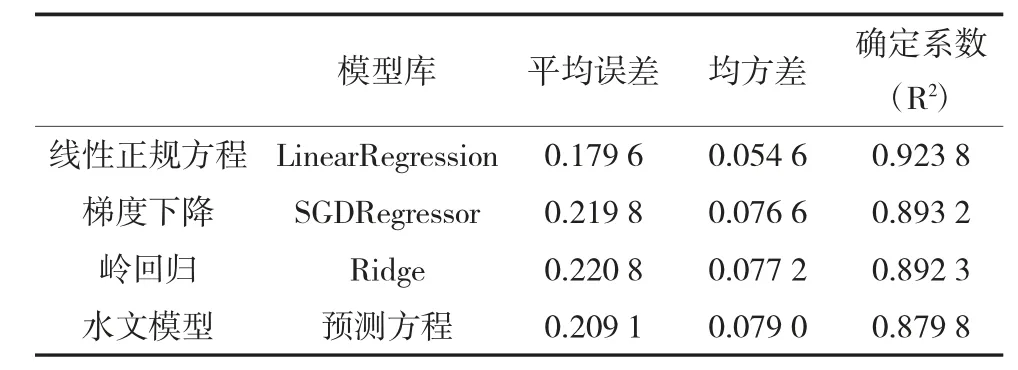
表2 各回歸模型預測評估結果表

根據以上各回歸模型預測評估結果可以看出，平均誤差、均方差、確定系數（R2）都相差不大，但從確定系數（R2）來評估各模型優劣，線性正規方程擬合效果最好，分別用測試集和各模型的預測值進行回歸曲線模擬。

其中中高水擬合較好，低水預測值較實測值偏高，主要是因為在低水期各出水斷面流量很小，受系統誤差、隨機誤差影響較明顯，并且黑虎泉白石橋斷面受下游船閘蓄防水影響較大。

根據2010—2021 年趵突泉水位時間序列，同時把水位曲線和根據實測水位預測泉群流量放置在一張圖上，見圖4，可直觀顯示各次實測流量與預測流量的比較，整體預測曲線擬合較好。

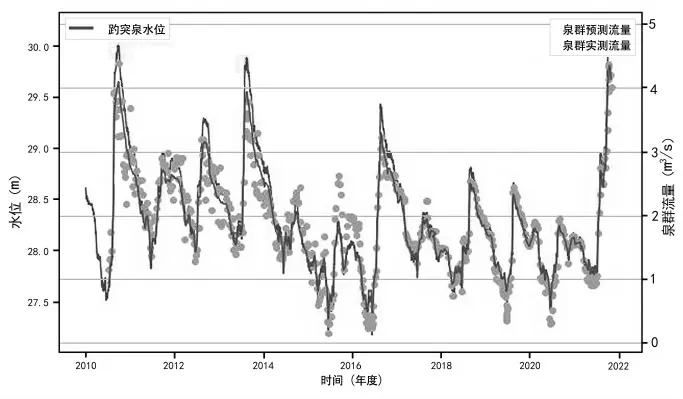
圖4 水位曲線與實測水位預測泉群流量擬合圖

3 結語

通過以上數據分析可以得出：趵突泉地下水位與四大泉群總流量具有高度線性相關性。通過機器學習對原始實測資料回歸分析，計算出趵突泉水位和泉群流量的線性方程式，模型庫可在實際工作中通過數據接口實時讀取遠端數據庫趵突泉地下水位信息，快捷高效計算出泉群出水流量，便于水位流量預測分析以及泉水利用。此外，隨著高中低水位實測流量頻次的不斷增加，可實時導入進預測分析模型，逐步提高回歸模型預測準確度。