一道向量試題的多角度探析

陳 余，龍佳慧，李林春

(貴州師范大學數學科學學院，貴州貴陽，550025)

1 試題呈現

( )

2 試題立意分析

2.1 考查基礎知識立意

《普通高中數學課程標準(2017年版)》要求學生理解平面向量的幾何意義和代數意義；掌握平面向量的概念、加法、減法、數乘運算、數量積運算和平面向量的基本定理以及平面向量的應用；能夠使用向量語言、方法對數學問題進行表述，同時可以運用向量的相關知識解決現實生活、物理或數學中的問題[1].本題綜合考查了平面向量、函數、不等式等內容，與《普通高中數學課程標準(2017年版)》的要求具有一致性.

2.2 考查思想方法立意

向量作為數與形之間的關鍵紐帶，能夠融數、形于一體，涉及的知識面較廣.向量通常與不等式、函數等整合解題，尤其在解決向量參數取值范圍這類題目時，經常借助函數的性質進行求解.本題重點考查了轉化與化歸思想、數形結合思想以及函數與方程思想.

3 解法探析

解法1坐標法+線性規劃

如圖1：以B為原點，BC所在直線為x軸，BA所在直線為y軸，建立平面直角坐標系[2]，設P點坐標為(x,y).

圖1 坐標法+線性規劃

則A(0,1),B(0,0),C(2,0),D(2,1),

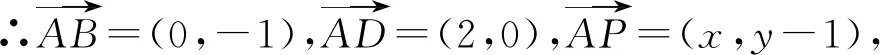
∵直線BD與圓相切，

∴直線l與圓有公共點，即圓心C到直線l的距離d≤r，

評析：本解法通過建立直角坐標系，從代數角度分析，將向量參數取值范圍的求解問題轉化為線性規劃問題.但是此類題型中有些約束條件會比較復雜，難以求解可行域，導致求解目標函數范圍時計算量偏大，效率不高.

解法2判別式法

化簡得：25x2-20(z+3)x+20z2-40z+84=0.

由解法1得：直線與圓有交點，方程有解，

∴z2-4z+3≤0，

∴1≤z≤3，

∴λ+μ≤3，故選A.

評析：本解法由解法1中直線與圓有交點得到啟發——利用判別式法求解.但在把直線方程代入圓方程求解△的過程中，計算量較大，容易出錯.

解法3參數方程(三角換元法)

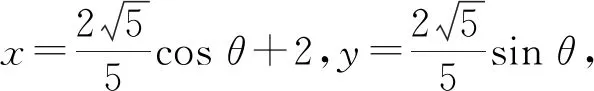
∵-1≤sin(φ-θ)≤1，

∴1≤sin(φ-θ)+2≤3，即1≤λ+μ≤3，故選A.

評析：本解法利用向量的特殊性，將幾何與代數進行巧妙轉化，為函數性質的運用奠定基礎，本題借助圓的參數方程、輔助角公式及三角函數的有界性進行求解，巧妙地突破了本題的難點，過程與解法1、2相比更加簡潔，便于學生理解.

解法4等面積法+橢圓參數方程

如圖2：過點C作CE⊥BD,交BD于點E,連接CE，

圖2 等面積法+橢圓參數方程

由等面積法得：

BC·CD=BD·CE，

∴sin(θ+φ)+2≤1+2=3，∴λ+μ≤3，故選A.

評析：在求解圓的半徑過程中，本解法區別于解法1中利用“點到直線的距離公式”，而是采用等面積法，過程更加直觀、算法更加簡潔.然后綜合運用橢圓的參數方程、輔助角公式及正弦函數的有界性進行求解，雖涉獵的知識領域較廣，但是便于理解，計算量較小.

解法5等和線法

補充：平面向量共線表達：

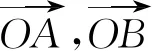
如圖3，當且僅當P點與E點重合時，λ+μ=1

圖3 等和線法

當P點位于其他位置時，

∴λ+μ=k(x+y),又∵E′、B、D三點共線，∴x+y=1，∴λ+μ=k，

所以需要做一個三角形與△ABD相似，并且相似比為k,并且經過P點，如圖3所示，所以λ+μ=k>1,

∴k最大時，λ+μ最大，即平移B′D′使之與圓相切于另一邊時最大，此時△AB″D″與△ABD的相似比為3.

∴k最大為3，∴(λ+μ)max=kmax=3，故選A.

評析：本解法借助等和線法找出參數取最大值時圓與直線的位置關系，根據三點共線巧妙地構造平行線，再利用三角形的相似比得出結果.此方法具有技巧性、過程簡潔，有利于學生解決此類復雜題型.

4 一題多變——多題一解

4.1 改變形狀

解析：∵O是三角形ABC的外心，

∴O在三角形的內部，假設該銳角三角形的外接圓的半徑為1，

∴λ+μ<-1或λ+μ>1，如果λ+μ>1，則O應該在三角形外部，

∴該三角形不是銳角三角形，與已知矛盾，則λ+μ<-1.

評析：本題僅僅將題目圖形改成平行四邊形，這樣更改之后的題目不適合使用建系進行處理，但是從等和線法的角度可以進行巧妙、快速的求解；本題的變式更加深入地表現了平面向量基本定理以及幾何意義和數形結合等基本方法和基本思想，更具有選拔功能.

解析：如圖4，延長AF、DE交于點M，延長AB、DC交于點N，則四邊形AMDN為菱形，當P點位于邊界CE上時，λ+μ取最小值，

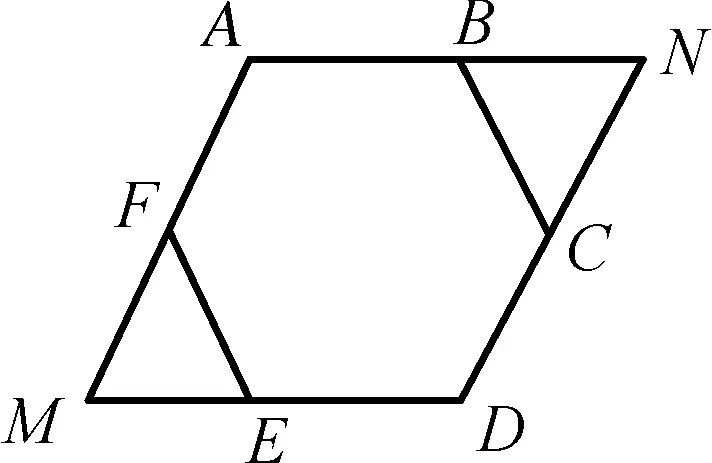
圖4

故此時λ+μ=3，即λ+μ的最小值為3.

4.2 改變形狀、條件及所求

解法2因為題目沒有特別說明△ABC是什么三角形，所以不妨設為等腰直角三角形，則立刻變為線性規劃問題，可快速求解(解法略).

( )

解析：(坐標法+三角函數)如圖5所示，以O為原點，OA、OB所在直線為x軸、y軸建立直角坐標系.

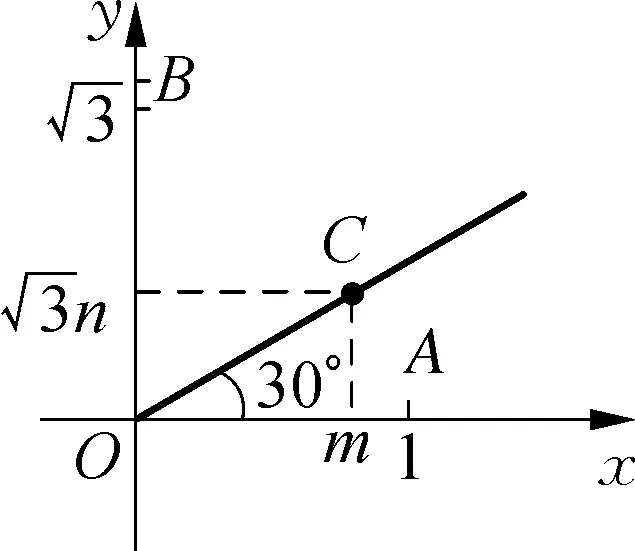
圖5

解析：建立如圖6所示的直角坐標系.

圖6

則A(-1，-1)，B(1，-1)，C(1，1)，D(-1，1)，

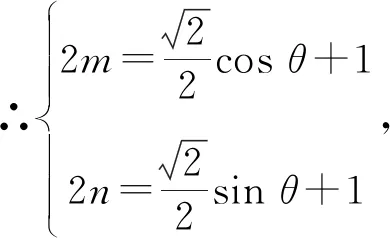
解析：如圖7，以A為原點，AB、AD所在直線為x軸、y軸建立直角坐標系.

圖7

則A(0,0),B(1,0),C(1,1),D(0,1).

化簡得：(x-1)2+(y-2)2=2.

得x=λ，y=μ，所以λ2+μ2=x2+y2表示圓(x-1)2+(y-2)2=2上的點到原點的距離的平方，其最大值等于圓心(1,2)到原點的距離加上半徑的平方，即

5 教學建議

一題多解是教師在數學教學活動中常用的手段和方式，對教師而言，一題多解既可以幫助教師提升解題能力，為啟發學生思考提供思路，也可以深入挖掘題目中涉及的基本知識、基本思想、數學模型等.對學生而言，一題多解可提升數學思維的靈活性和發散性，幫助學生發現數學問題的本質，進一步提升分析問題、解決問題的能力.一題多解不是教學的目的，是培養學生創新思維的有效途徑，變式和推廣還可發散學生的思維，培養學生的應用意識.教師在教學中應注重引導學生多角度思考、分析問題，關注數學知識的整體性，滲透數學思想方法，培養數學核心素養.