重夸克勢能模型中非微擾貢獻重要性的定量研究

唐愛琪，楊 航，孫亞男

（廣西師范大學物理科學與技術學院，廣西 桂林 541004）

1 引言

近數十年，物理學家們一直都在尋找脫離禁閉狀態的夸克膠子物質，但夸克膠子物質存在需要非常嚴苛的條件，例如要在體系的溫度或者重子數密度要非常的高才可以存在。在地球，我們可能達到嚴苛條件的可能只有相對論重離子碰撞試驗。在進行重離子碰撞時，會產生處于熱平衡的物質稱它為“夸克-膠子等離子體”(QGP)，即QGP 產生于碰撞初期。又因為，體系本身會發生膨脹，而導致體系的溫度下降，因此QGP 會因溫度的降低而演化為強子氣體凍出，從而導致我們最終探測器探測到的都是末態的強子，即我們是無法直接觀測到QGP 的！在重離子碰撞試驗中，我們無法之間觀測到夸克膠子等離子體，我們觀察到的是末態的強子氣體。在實驗上就只能去分析這些末態的粒子，當然也需要依靠可靠的理論數據計算。對碰撞早期物質狀態敏感的末態粒子稱為“QGP 的探針”。[1]本文我們重點利用的探針為：重夸克偶素。由于“重夸克偶素”的質量比較大，相對論效應比較弱，所以，通過非相對論下的薛定諤方程，我們可以很好的去研究“重夸克偶素”性質，通過求解薛定諤方程，我們可以得到“重夸克偶素”的束縛能和本征能。因此，構建出能夠很好描述“重夸克偶素”性質的重夸克勢能模型對研究重夸克偶素的物理性質是非常重要的。本文將利用由Karsch，Mehr 和Satz 等人引入、郭云教授改進的的重夸克勢能模型（以下簡稱“改進拓展的KMS 重夸克勢能模型”）為代表，來進行重夸克勢能模型中非微擾貢獻重要性的定量研究。

2 改進拓展的KMS 重夸克勢能模型簡述

2.1 原始KMS 重夸克勢能模型推導及介紹

由于組成重夸克偶素的夸克的質量較大，相對運動速度比較小，因此，當粗暴的假設夸克與反夸克之間的相互作用力是一個簡單的靜態勢時，就可以應用非相對論來近似。

第一個著名的勢模型是Cornell 勢：

其中，αs是強相互作用的耦合常數，σ是弦強度，r 是夸克與反夸克之間的距離。零溫度下的Cornell勢由微擾部分和非微擾部分的唯象模型σr兩部分構成。1988 年，由F.Karsch,M.T.Mehr 和H.Satz 開創性的模仿零溫度下Cornell 勢，引入了有限溫度下的簡單的勢能模型，稱為原始的KMS 重夸克勢能模型。

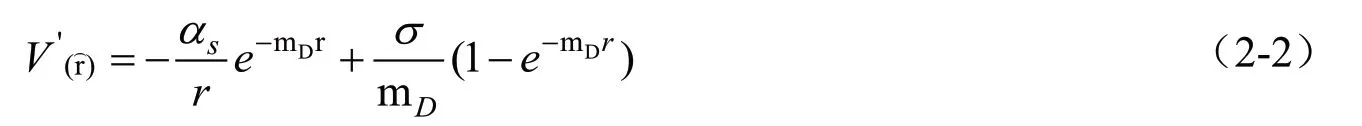
其中德拜質量mD是與溫度有關的函數，我們可以看到在有限的溫度下，勢能（2-2）式表示的重夸克勢能為指數的形式。且通過與格點數據進行對比，Karsch 等發現，原始的KMS 重夸克勢能模型是能夠與格點數據中的自由能數據擬合良好。

當德拜質量mD→0時，則有

我們發現。此時的勢能公式與零溫度時的Conell 式的形式一模一樣！

2.2 改進拓展的KARSCH-MEHR-SATZ 重夸克勢能模型的介紹與探索

在2007 年，M.Laine 等人首次提出重夸克勢能模型有虛部并將有限溫度下的重夸克勢能模型表示成復值的形式后，KMS 重夸克勢能模型也在不斷的發展、變化。實際上，2.1 中提到的（2-2）式就是原始的KMS重夸克勢能模型，它可以去定性的描述格點數據，但引起物理學家思考的是：重夸克偶素的質量并不都是足夠大的，如粲夸克偶素或底夸克偶素，它們在非相對論的極限下并不能使用微擾勢能去描述其間的相互作用，所以，一個包含非微擾項的勢能形式脫穎而出了。為描述非微擾的影響，2019 年，郭云教授等借助E.Megias等人提及的二維膠子凝聚的貢獻，嘗試提出解決的方法：在微擾（延遲）膠子傳播子中加入了一個新的唯象式。[錯誤!未定義書簽。]通過傅里葉變換即可得到擴展的KMS 重夸克勢能模型的實部具體形式如下：

同理，擴展的KMS 重夸克勢能模型虛部具體形式如下：

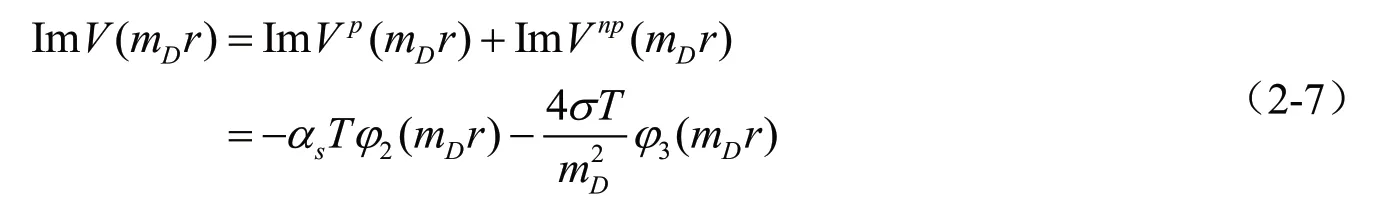
其中:

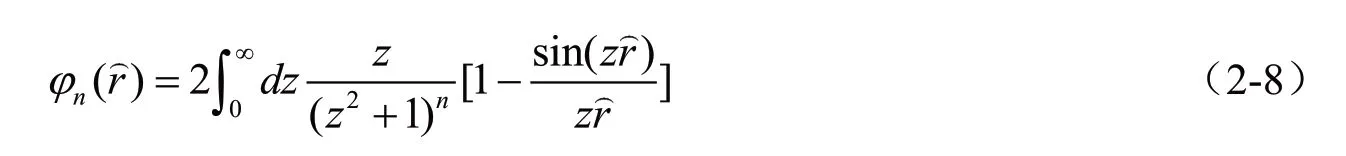
即VKMS=ReV+iImV，為擴展的KMS 勢能模型。

那么擴展的KMS 勢能模型得到的數據能否在格點數據范圍內呢？2017 年，Y.Burnier 和A.Rothkopf 發表了擁有淬火QCD 格點數據的文章，與擴展的KMS 勢能模型擬合情況如圖1、圖2：

圖1 淬火QCD格點數據（藍點）和擴展KMS勢能模型中的實部ReV的比較，其中，ReV由紅實曲線表示，只考慮微擾貢獻的由黑虛曲線表示。[1]

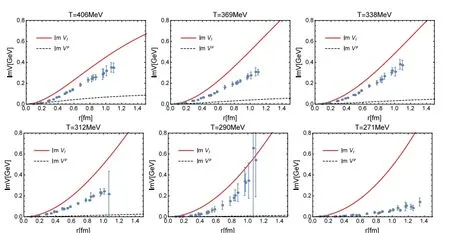
圖2 淬火QCD格點數據（藍點）和擴展KMS勢能模型中的實部ImV的比較，其中，ImV由紅實曲線表示，只考慮微擾貢獻的由黑虛曲線表示。[2]

通過圖1 和圖2 可以發現：擴展KMS 重夸克勢能模型的實部部分與格點數據擬合的很好，且當距離較大時的行為明顯是夸克禁閉的行為；但擴展KMS 重夸克勢能模型的虛部部分在隨著r 的增大，發生集聚增大的變化并超過了格點數據。雖擴展的KMS 模型虛部擬合效果不如人意，但仍比只考慮微擾貢獻有了明顯進步，這也提醒我們，目前擴展的KMS 勢能模型，特別是虛部部分仍然需要進行進一步的改進。

幸運的是，在對擴展的KMS 重夸克勢能模型與淬火QCD 格點數據擬合情況并不滿意后，為了更好的符合格點數據的虛部部分，郭云教授等繼續又對擴展的KMS 重夸克勢能模型進行了再一次的改進，改進思路在非微擾項中在二維膠子傳播子中繼續加入新的貢獻，并同樣再進行傅里葉變換，即可得到改進拓展KMS重夸克勢能模型。

具體形式如下：

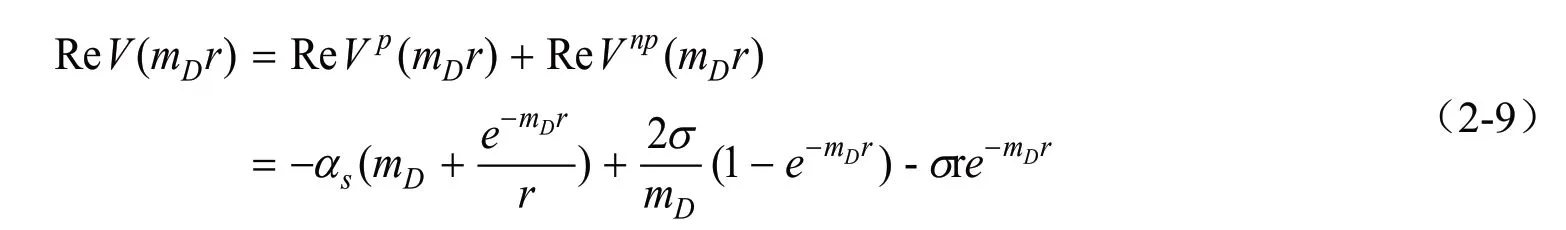
同理，改進擴展的KMS 重夸克勢能的虛部具體形式如下：

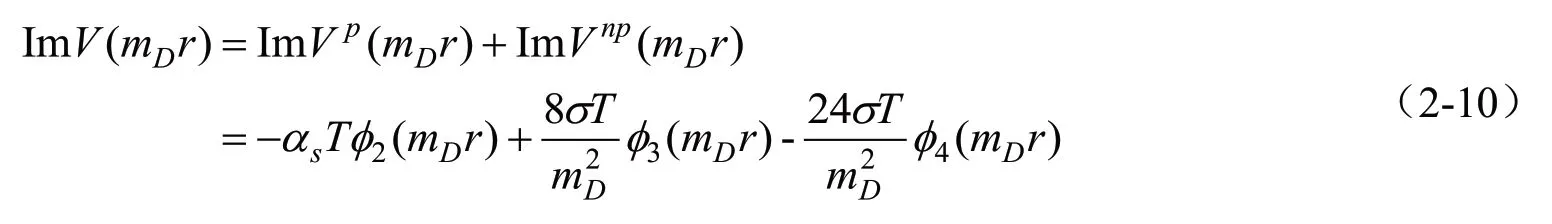
其中:

又，考慮到夸克的質量mQ有限，為提高解得的夸克態波函數的精度，選擇加入一個與成比例而與自旋無關的一個修正值。即，為改進擴展的KMS 重夸克勢能模型最終形式，如（2-12）式。同樣與淬火QCD 格點數據進行對比，發現在實部擬合依然很好的情況下，虛部部分的擬合也有了很大的改進[2]。

現在，我們通過將（2-9）式帶入薛定諤方程，即可求出重夸克偶素的本征能，我們將利用mathmatica程序，對改進拓展的KMS 重夸克勢能模型帶入薛定諤方程進行計算以獲得重夸克偶素的本征值。

我們可以看到（2-12）式包含微擾項和非微擾項，為了去探索改進拓展的KMS 重夸克勢能模型中非微擾貢獻重要性，我們選擇將σ=0時的改進拓展的KMS 重夸克勢能模型，如（2-13）式，并同樣利用mathmatica程序將其帶入薛定諤方程以獲得無非微擾時重夸克偶素的本征值。

當σ=0時，

通過改重變溫度和夸克偶素的質量可以得到兩種情況下對應不同溫度、不同質量的相應本征能。通過的兩種情況對比，我們可以得到，當重夸克偶素的質量達到多少時，非微擾不再影響本征能的值，達到定量研究改進拓展的KMS 重夸克勢能模型中非微擾貢獻重要性的目的

3 實驗結果

我們利用mathmatic程序，對改進拓展的KMS重夸克勢能模型進行計算，并計算了多種溫度下不同質量的下的本征能，利用數據所畫圖像如圖3所示。

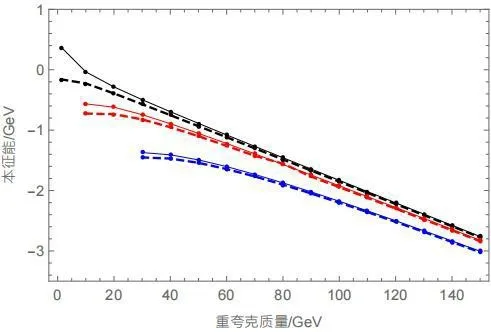
圖3 黑色曲線為溫度0.192*1.1GeV時，其中黑色虛線代表σ=0時本征能隨質量的變化，黑色實線代表σ=0.215時本征能隨質量的變化；紅色曲線為溫度0.192*5.0GeV時，其中紅色虛線曲線代表σ=0時本征能隨質量的變化，紅色實線代表σ=0.215時本征能隨質量的變化；藍色曲線為溫度0.192*10.0GeV時，其中藍色虛線代表σ=0時本征能隨質量的變化，藍色實線代表σ=0.215時本征能隨質量的變化。

4 結論

通過圖3 的橫向的對比，我們發現在同一溫度下，隨著重夸克質量的升高非微擾部分對通過重夸克勢能模型得到的本征能的影響逐漸降低，當重夸克質量一定程度時(如溫度為0.192*1.1GeV，重夸克質量為50GeV 時），非微擾部分基本不能再影響本征能的值。

即，我們可以得到結論：當重夸克質量一定程度時(如溫度為0.192*1.1GeV，重夸克質量為50GeV 時），非微擾部分不能再影響重夸克本征能的值。

而我們知道，實際上，像b夸克偶素態這樣的最大的夸克質量也僅為4.7GeV，顯然在現實中，重夸克勢能模型中的非微擾貢獻是非常重要、不能被忽略的！