BP神經(jīng)網(wǎng)絡(luò)在水泥土無側(cè)限抗壓強度預(yù)測中的應(yīng)用
蔡金軒 孟凡星
(長江大學(xué),湖北 荊州 434023)
0 引言
軟土具有高壓縮性、低承載力及低抗剪強度等特點。為防止因地基軟土而造成不均勻沉降,高層建筑使用水泥土來改善地基條件[1]。影響水泥土強度的因素有很多[2-3],且存在著復(fù)雜的非線性關(guān)系。國內(nèi)外學(xué)者提出過經(jīng)驗公式、數(shù)值模擬預(yù)測方法,但存在結(jié)果不精確的局限性。BP神經(jīng)網(wǎng)絡(luò)因自身較強的自學(xué)習及自適應(yīng)能力,已廣泛應(yīng)用于擬合、壓縮、預(yù)測、分類等[4],其具有較強的映射能力,在抗壓強度預(yù)測方面表現(xiàn)優(yōu)異[5-7]。Tang等[8]基于神經(jīng)網(wǎng)絡(luò)使用經(jīng)驗?zāi)P头治鲋阅艿挠绊懸蛩亍=钩艿龋?]分析植生型多孔混凝土抗壓強度的主要因素,采用神經(jīng)網(wǎng)絡(luò)建立預(yù)測模型,對模型預(yù)測值及線性回歸方程計算值進行對比。宋軍偉等[10]利用遺傳算法對BP神經(jīng)網(wǎng)絡(luò)進行優(yōu)化,在多元摻和料砂漿28 d抗壓強度的預(yù)測上表現(xiàn)優(yōu)異。本研究通過大量室內(nèi)試驗得到不同水泥摻量、水泥種類、水灰比及標號在不同凝期下的抗壓強度,并在此基礎(chǔ)上采用BP神經(jīng)網(wǎng)絡(luò)對水泥土無側(cè)限抗壓強度進行預(yù)測分析。
1 無側(cè)限抗壓強度試驗
1.1 試驗材料
試驗選用典型的淤泥質(zhì)粉質(zhì)黏土,參照《土工試驗方法標準》[11]進行物理力學(xué)性質(zhì)試驗,如表1所示。該試驗所用水泥為華新水泥股份有限公司生產(chǎn)的P·O42.5、P·C42.5及M32.5。
1.2 試樣制備
參照《水泥土配合比設(shè)計規(guī)程》[12]對試驗的試樣攪拌、成型及養(yǎng)護進行統(tǒng)一操作。原狀淤泥質(zhì)土含水量高,初始進行自然風干,之后將風干的土樣放置干燥箱進行干燥處理(110℃,不小于8 h),然后將風干后的土樣進行粉碎處理,并通過2 mm篩,最后將過篩的土按照試驗進行配比。采用機械攪拌,在攪拌結(jié)束后20 min內(nèi)將土樣澆筑到模具中,并在振動臺上進行振實處理。將試樣表面覆膜放入標養(yǎng)室中,進行恒溫養(yǎng)護(20℃±2℃、濕度≥95%),24 h后進行脫模,最終將其轉(zhuǎn)至標養(yǎng)室養(yǎng)護至相應(yīng)齡期。
1.3 試驗儀器及方法
試驗基于《水泥土配合比設(shè)計規(guī)程》[12],選取15%為水泥摻入比基準值,分別設(shè)計10%、15%、20%三種水泥摻入比及0.5、0.75、1.0三組水灰比,對凝期為7 d、14 d、28 d的試樣進行水泥土無側(cè)限抗壓強度試驗。采用上海松盾儀器制造有限公司生產(chǎn)的WDW-1電子萬能試驗機,依據(jù)規(guī)范要求[11]來調(diào)配好相關(guān)參數(shù)(應(yīng)力控制為0.15 kN/s),進行試樣加載。通過室內(nèi)試驗,獲得不同水泥型號、水泥摻入量、水灰比在不同凝期下的抗壓強度指標,見表2。
2 神經(jīng)網(wǎng)絡(luò)基本理論
2.1 神經(jīng)網(wǎng)絡(luò)基本理論
BP神經(jīng)網(wǎng)絡(luò)全稱為誤差反向傳播神經(jīng)網(wǎng)絡(luò),其屬于多層前向型網(wǎng)絡(luò),能以任意精度逼近任何非線性函數(shù)[13],采用BP神經(jīng)網(wǎng)絡(luò)對水泥土單軸抗壓強度進行預(yù)測時,要選取適合的輸入特征。當水泥型號相同時,水泥土強度隨凝期的增長而逐漸增大,隨著水泥摻入量的增加,水泥土單軸抗壓強度得到提高[14-16]。研究發(fā)現(xiàn),水灰比對水泥土強度有較大的影響[17],因此選取水泥種類、標號、凝期、水灰比、水泥摻入量作為預(yù)測水泥土強度模型的輸入特征。神經(jīng)網(wǎng)絡(luò)數(shù)據(jù)來源室內(nèi)無側(cè)限抗壓強度試驗的135個試樣。考慮到試驗水泥種類不同,將P·O42.5水泥賦值為1、P·C42.5水泥賦值為2、M32.5水泥賦值為3,根據(jù)水泥標號不同,將標號42.5賦值為4.25、標號32.5賦值為3.25。
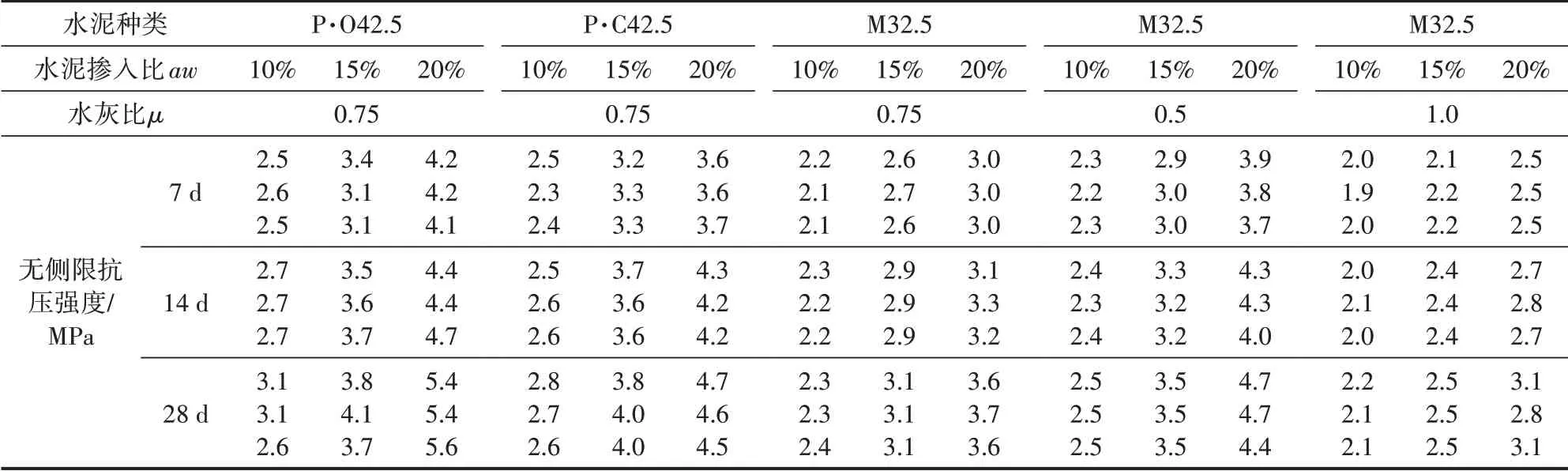
表2 水泥土無側(cè)限抗壓強度指標
在神經(jīng)網(wǎng)絡(luò)模型預(yù)測中,輸入層包含種類、標號、摻入量、水灰比、凝期的輸入特征。輸出層特征選取為試樣的抗壓強度,選用log-sigmoid函數(shù)作為輸入層與輸出層的傳輸函數(shù),選取tansigmoid作為函數(shù)隱含層與輸出層的激活函數(shù)。
由于傳輸函數(shù)選取的是log-sigmoid函數(shù),見式(1),其本身只能識別0~1的值,函數(shù)在[0,1]內(nèi)曲線變化平緩。因此,在神經(jīng)網(wǎng)絡(luò)訓(xùn)練前,對數(shù)據(jù)進行歸一化處理,將數(shù)據(jù)值控制在該區(qū)間內(nèi),從而使該函數(shù)在此區(qū)間變化梯度較大,提高網(wǎng)絡(luò)收斂速度。數(shù)據(jù)歸一化的方法選最大最小法[18],見式(2)。

式中:x為向量矩陣的數(shù)據(jù);φ(x)為函數(shù)傳遞值;X K為歸一化的數(shù);Xmin為數(shù)據(jù)序列最小數(shù);Xmax為序列最大數(shù)。
2.2 BP神經(jīng)網(wǎng)絡(luò)模型的建立
在建立模型前,先確定隱含層神經(jīng)元的個數(shù),隱含層神經(jīng)元數(shù)目的選擇是比較復(fù)雜的問題,往往根據(jù)設(shè)計者的經(jīng)驗及多次試錯來確定,沒有明確的解析式能推導(dǎo)出建立模型所需的神經(jīng)元個數(shù)。關(guān)于隱含層神經(jīng)元的個數(shù)確定[4]可參照經(jīng)驗公式(3)。

式中:n1為神經(jīng)元個數(shù);m為輸出神經(jīng)元個數(shù);n為輸入單元數(shù);a為[1,10]內(nèi)的常數(shù)。
本研究的輸出神經(jīng)元個數(shù)為1個,輸入單元數(shù)為5個,則隱含層神經(jīng)元的個數(shù)為[4,13],最優(yōu)神經(jīng)元個數(shù)要在該范圍通過多次試算才能確定。
在神經(jīng)網(wǎng)絡(luò)訓(xùn)練中,訓(xùn)練樣本的數(shù)目越多,則訓(xùn)練結(jié)果越能反映其內(nèi)在規(guī)律,本研究選取的樣本總量為135個,軟件隨機選取95個樣本,并將其隨機劃分為70%的訓(xùn)練樣本、15%的測試樣本及15%的驗證樣本,剩余的作為預(yù)測指標。選取均方差MSE(Mean Square Error)作為神經(jīng)網(wǎng)絡(luò)終止訓(xùn)練的準則,通過M SE來反映神經(jīng)網(wǎng)絡(luò)的性能及神經(jīng)網(wǎng)絡(luò)的精度。均方差越小,則網(wǎng)絡(luò)性能越好,精度越高。采用R2來反映訓(xùn)練樣本、測試樣本、預(yù)測樣本及總樣本的輸出與目標間的相關(guān)性。
不同神經(jīng)元個數(shù)下試算的M S E值和R值如圖1、圖2所示。由圖1、圖2可知,該BP網(wǎng)絡(luò)結(jié)構(gòu)在為5-8-1時MSE值最小、R值最大,預(yù)測的精度較高且比較穩(wěn)定。因此,用于水泥土強度預(yù)測的神經(jīng)網(wǎng)絡(luò),其隱含層神經(jīng)元為8個。

圖1 不同神經(jīng)元下的MSE值

圖2 不同神經(jīng)元下的R值
2.3 回歸及預(yù)測結(jié)果
圖3為BP神經(jīng)網(wǎng)絡(luò)模型性能圖,該圖反映了網(wǎng)絡(luò)的驗證性能,向量的訓(xùn)練在保證誤差最小的前提下進行驗證,從而防止出現(xiàn)過擬合。由圖3可知,該模型最佳驗證性能在訓(xùn)練次數(shù)為3時取得,且該神經(jīng)元模型的M S E值為0.001 070 8。
BP神經(jīng)網(wǎng)絡(luò)模型的訓(xùn)練階段如圖4所示,誤差在第3次訓(xùn)練后重復(fù)出現(xiàn),而在第4次訓(xùn)練停止測試過程沒有出現(xiàn)錯誤。因此,可將該時期的權(quán)重當作最終權(quán)重。
采用BP神經(jīng)網(wǎng)絡(luò)模型對該水泥土強度相關(guān)試驗數(shù)據(jù)進行訓(xùn)練,回歸結(jié)果如圖5所示,分別反映訓(xùn)練、驗證、測試及總體結(jié)果。當R值越接近1,越能表示輸出及目標間具有良好的線性關(guān)系。該訓(xùn)練樣本、驗證樣本、測試樣本及總體樣本的R值分別為0.985 81、0.989 75、0.980 04、0.985 51,表明總體上線性回歸的結(jié)果較好,采用該模型對水泥土強度進行預(yù)測結(jié)果較為可靠。
在對模型進行反復(fù)訓(xùn)練后,神經(jīng)網(wǎng)絡(luò)模型能準確預(yù)測出水泥土的無側(cè)限抗壓強度,得到的水泥土強度預(yù)測結(jié)果對比見圖6。由圖6可知,通過神經(jīng)網(wǎng)絡(luò)對樣本進行訓(xùn)練預(yù)測,室內(nèi)試驗數(shù)據(jù)指標線條與預(yù)測線條基本相似,從預(yù)測的40個樣本可以發(fā)現(xiàn),相對誤差最小僅為0.59%,最大為19.54%,對其他結(jié)果進行預(yù)測,其相對誤差均小于20%。因此,在該網(wǎng)絡(luò)模型條件下輸出的參數(shù)合理。

圖3 BP神經(jīng)網(wǎng)絡(luò)模型性能

圖4 BP神經(jīng)網(wǎng)絡(luò)模型訓(xùn)練狀態(tài)

圖5 BP神經(jīng)網(wǎng)絡(luò)模型回歸R值
3 結(jié)論
本研究采用BP神經(jīng)網(wǎng)絡(luò)模型,選用水泥種類、標號、凝期、水灰比、水泥摻量作為輸入特征,通過室內(nèi)試驗得到水泥土無側(cè)限抗壓強度,并進行訓(xùn)練預(yù)測,得到以下結(jié)論。①BP神經(jīng)網(wǎng)絡(luò)的M S E值約為0.001 152 4,R值約為0.988,該網(wǎng)絡(luò)模型水泥土無側(cè)限抗壓強度能進行較高精度的預(yù)測。②網(wǎng)絡(luò)模型中有90%的數(shù)據(jù)誤差范圍在10%以內(nèi),表明BP神經(jīng)網(wǎng)絡(luò)適用于提取輸入特征,能較好地映射水泥土無側(cè)限抗壓強度與影響因素間的非線性關(guān)系。③采用BP神經(jīng)網(wǎng)絡(luò)能快速、準確地預(yù)測水泥土無側(cè)限抗壓強度,能在一定程度上減小室內(nèi)試驗的工作量,從而節(jié)省時間及試驗成本。

圖6 水泥土抗壓強度預(yù)測結(jié)果對比

