顧及動態介數優先的城市路網抗毀性分析

黃丞甫，劉 剛,2，牟 標

（1.成都理工大學地球科學學院，四川成都 610059；2.地質災害防治與地質環境保護國家重點實驗室(成都理工大學)，四川成都 610059）

城市道路網絡是城市社會經濟運行的重要載體，同時也是城市空間形態結構特征的體現，其可靠性或者抗毀性直接關系到城市的安全和可持續發展.城市交通系統功能對維持城市生態系統至關重要[1].面對隨機事件（如突發災害、交通事故、交通擁堵等）或者惡意攻擊（即人為蓄意破壞關鍵道路），路網的連通性或者性能都會受到不同程度的影響，故如何系統分析實際路網的抗毀性一直以來都是復雜網絡、交通、地理信息系統等研究的熱點和重點問題[2-8].

近年來，學者們針對不同復雜系統的抗毀性進行了廣泛討論[9-11].研究認為，具有無標度特性的復雜網絡系統，其抗毀性表現出“魯棒而又脆弱”的特征，即面對隨機攻擊具有很強的魯棒性，但對于蓄意攻擊卻又非常脆弱[12].隨機攻擊大量節點，無標度網絡可能仍然能保持全局連通；但惡意攻擊少量節點，就可能破壞網絡的整體連通性并導致系統癱瘓[13-14].公路網的脆弱性表現為運行狀態脆弱性和結構脆弱性，可以從網絡拓撲結構和運行狀態兩個因素角度評價路網的整體脆弱性[15-17].從連通度、最大連通子圖、網絡效率等角度，相關研究探討了公路網按節點度、點介數和邊介數大小進行攻擊的魯棒性[4].從拓撲結構上，連接度和介數中心性都能較好地描述節點或者邊在網絡中的重要性[18].研究表明，對于公路交通網絡，無論是攻擊節點還是邊，考慮介數優先的攻擊策略引起網絡功能下降速度最快，攻擊效果更好，因此廣泛用于路網的魯棒性分析[19].在攻擊策略的選擇中，Holme采用了四種不同的攻擊策略：根據移除過程中初始網絡或當前網絡的度和介數中心性降序進行移除.研究發現，動態計算的度和介數中心性的攻擊策略，往往比基于初始網絡的攻擊策略更有害[20].聶廷遠等在此基礎上探尋了度和介數的相關性，并應用基于初始網絡和動態計算的兩種攻擊策略驗證了其效率[21].在抗毀性度量指標方面，平均測地線距離、最大連通子圖和網絡效能都是常用的評價指標，而網絡效能指標在道路網絡分析中具有顯著優勢，其評價效果優于平均路徑長度、連通度等指標，進而得到廣泛應用[22].

路網抗毀性分析主要是研究路網在不同攻擊強度下網絡功能的變化，惡意攻擊更能揭示重要道路的破壞對路網整體功能的影響.然而，針對城市路網的抗毀性分析，現有的惡意攻擊方法主要還是從道路或者節點的原始中心性來考慮其重要度，即基于靜態中心性的攻擊策略.以介數中心性為例，傳統方法關注靜態介數情況下的惡意攻擊，沒有考慮攻擊過程中節點或者邊介數中心性的變化，導致攻擊的目標可能并非當前網絡中介數中心性最大的或者最重要的.原始路網中所有道路的介數中心性是確定的，但遭受攻擊后，剩余路網的拓撲結構將發生改變，故道路的中心性或重要性也將隨之變化.惡意攻擊的思想是破壞路網中最為關鍵的道路，如果整個過程都是按照原始路網的介數中心性進行攻擊，難以保證后續攻擊的道路是當前路網中最為重要的.

為此，本文將從節點和邊的介數中心性角度，顧及在攻擊過程中介數中心性的變化，提出基于動態介數優先的公路網抗毀性分析方法.通過動態計算每次攻擊后當前網絡上所有元素的介數，重新評估節點或者邊的重要性，進而確保每次惡意攻擊都移除的是當前網絡中最為重要的節點或者邊，提升惡意攻擊的效果，為路網抗毀性分析提供更為科學的參考依據.

1 復雜路網模型拓撲表達方法

為深入研究路網的抗毀性情況，本文利用復雜網絡理論從尺度角度設計了兩種交通網絡模型：基于道路-道路關系的路網拓撲模型、基于節點-節點關系的路網拓撲模型.傳統的幾何路網模型雖然較好地保留了路網空間形態結構，但不便于利用復雜網絡理論研究其拓撲結構特征及實施交通流等動態過程的模擬.同時，外部攻擊對路網的破壞可能也存在尺度上的不同，比如單次攻擊可能只破壞一個路口（節點）或者一個路段，也可能破壞整條道路.所以，從單次攻擊尺度上研究路網在不同攻擊尺度下的性能變化，能更加準確刻畫路網的抗毀性.

圖1所示是兩種路網拓撲模型的建模原理.在基于道路-道路關系的路網拓撲模型中，將一條道路抽象為一個節點，如果兩條道路相互連接，則在二者對應的兩個節點之間產生一條邊[23-24].在基于節點-節點關系的路網拓撲模型中，幾何路網中的節點對應于該拓撲模型的節點，路段對應于模型中的邊且其權重即等于路段的長度.對于前者而言，采用的是對偶圖的方式進行復雜路網建模，有助于分析道路之間的連接關系以及整個路網的連通性.對于后者而言，可以準確地計算路網上每個路口和路段的中心性情況.

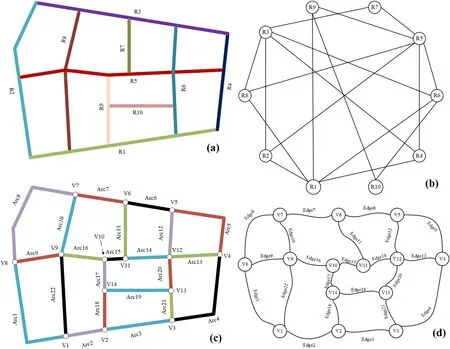
圖1 路網拓撲表達方法Fig.1 Topological representations of an urban road network

2 基于動態介數優先的城市路網抗毀性分析方法

復雜網絡的抗毀性指網絡功能在各種攻擊策略下持續作用的能力，通常被定義為網絡上部分節點或邊失效后網絡整體性能的下降值.理論上，隨著公路網上越來越多的節點或者路段失效，路網的整體性能必然呈連續下降趨勢.因此，為評價路網的抗毀性，必須對網絡的功能或者性能進行合理的度量.傳統方法常用網絡的平均路徑長度（L）來度量網絡的功能：

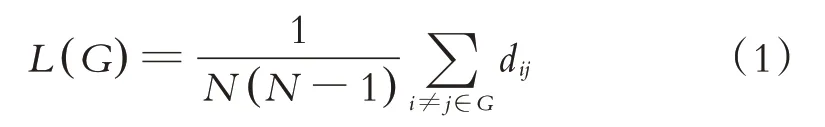
在由N個節點和K條邊組成的網絡G中，dij表示從節點i到j所需要經過邊的最小次數，在網絡節點或邊被毀壞后，平均路徑長度會增大，故網絡抗毀性就可以由平均路徑長度的增加值來衡量.顯然，平均路徑長度增加越多，說明網絡整體的連通度越不好，所以網絡性能顯著下降，其抗毀性就越差.然而，實際研究表明，利用平均路徑長度表征網絡功能變化存在明顯缺失，因為隨著破壞程度的加劇，平均路徑長度呈現“先增后減”的趨勢，主要是由于攻擊后期網絡規模太少導致的，故從全局意義上平均路徑長度不適宜用于網絡的抗毀性分析[15].研究發現，網絡整體效能指標在刻畫網絡抗毀性分析方面具有更加顯著的優勢，該指標描述的網絡性能隨攻擊程度呈穩定連續下降趨勢.故本文利用該指標進行網絡抗毀性分析.

2.1 網絡整體效能指標

為準確刻畫路網在遭受不同程度破壞下整個網絡的抗毀性情況，利用網絡整體效能(E()G)指標來進行網絡抗毀性的定量分析.一般地，兩個節點之間的效能定義為該兩點之間時間或距離的倒數：

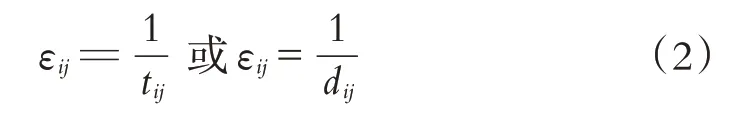
式中：εij為節點i和j之間的效能，tij為從節點i和j之間的時間成本，dij為兩個節點之間的距離成本.這里，默認以距離成本進行效能計算.

則E(G)定義為該網絡上所有節點對間效能的平均值：

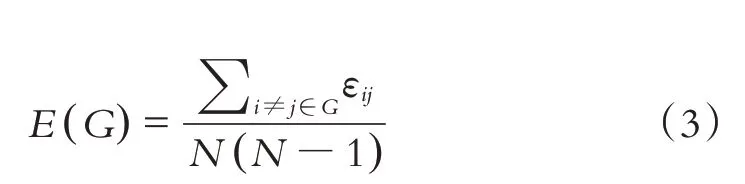
式中：E(G)為網絡G的整體效能，N為網絡節點個數.網絡整體效能指標廣泛應用于網絡抗毀性分析，效果優于網絡的平均最短路徑長度等指標，避免了其他指標隨網絡破壞程度的加大出現的先變大后變小的缺陷，保證路網抗毀性分析的穩定性和準確性.

2.2 基于動態介數優先的城市路網抗毀性分析算法

2.2.1 基本思想

路網的抗毀性分析通常研究路網在隨機攻擊和惡意攻擊兩種模式下網絡性能的變化.隨機攻擊是隨機破壞路網上的節點、道路或者路段，惡意攻擊一般是破壞路網上連接度較大、介數中心性較大等相關重要的節點、道路或者路段.針對惡意攻擊，現有方法是通過對原始路網的所有節點或路段按照某個中心性指標進行重要度排序，然后按重要度從高到低進行攻擊.

對于原始路網而言，對節點或者道路的中心性排序確實可以客觀地描述其重要程度.然而，在實施惡意攻擊后，路網上節點或者道路的中心性將發生變化，難以保證后續攻擊的目標為當前網絡中最重要的節點或道路，因此動態計算網絡元素的重要度并作為下一次攻擊的依據更能體現惡意攻擊的總體思想和目標.

為進一步闡述該方法，本文設計了一個示意圖（圖2）以及利用該方法攻擊節點后路網上節點重要度（基于介數中心性）排序的變化情況（表1）.

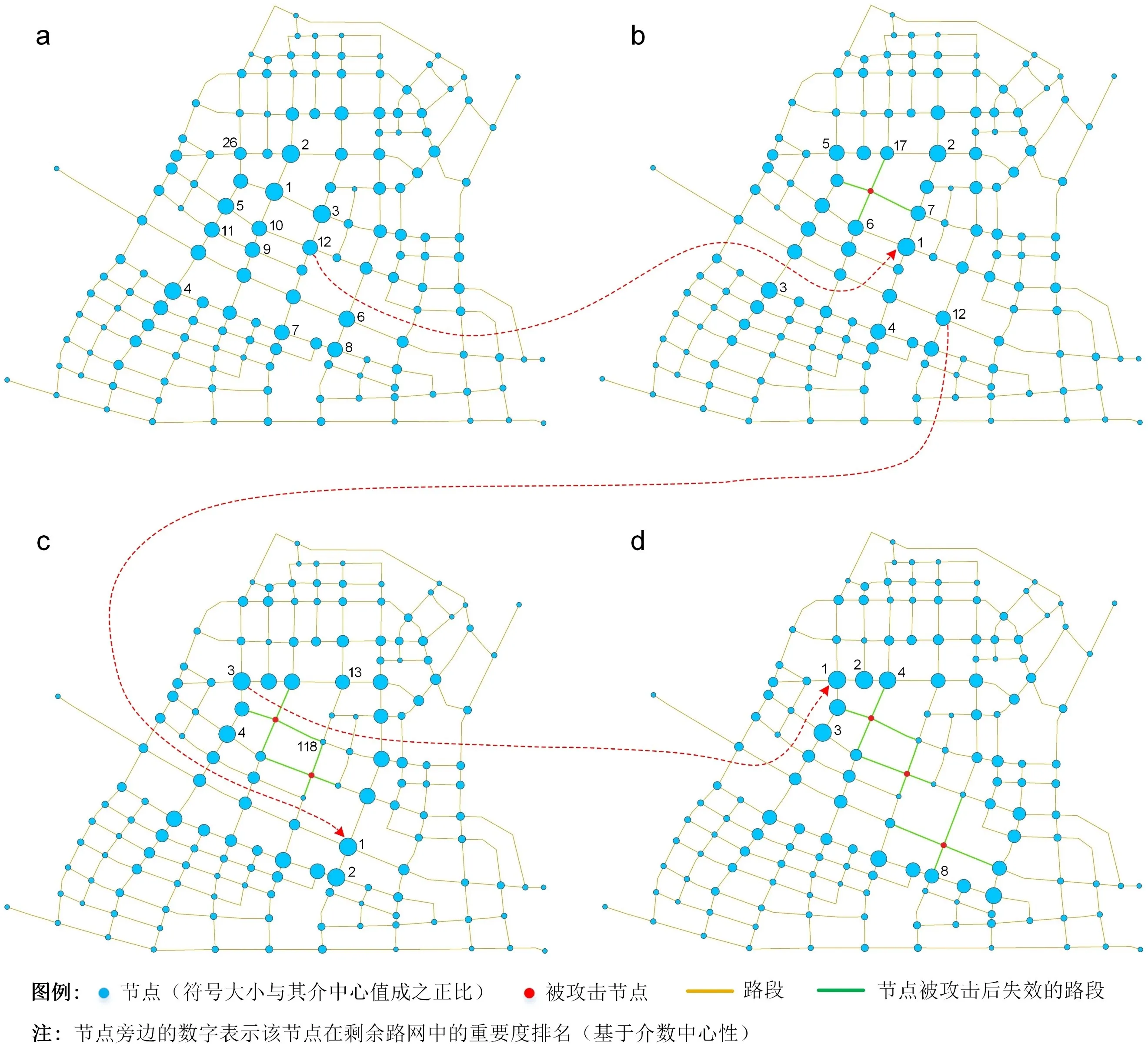
圖2 介數中心性動態變化的方法示意圖Fig.2 Schematic diagram of method based on dynamic changes of betweenness centrality

根據圖2和表1可知：當65號節點被攻擊后，在原始路網（圖2a）中介數中心性排名第2的節點（編號68），其動態介中心值排名在剩余路網（圖2b）中排名下降到第17位，而在原始路網中排名第12位的節點（編號76）上升到第1位；當76號節點被攻擊后，在圖2b路網中重要度排名第2的節點（編號89）在剩余路網（圖2c）中下降到第13位，而之前排名第12的節點（編號94）上升到第1位；當94號節點被攻擊，圖2c中排名第2的節點（編號87）在剩余路網（圖2d）中下降到第8位.經過三次攻擊，編號為48的節點從原始路網中排名26上升到排名第1，即圖2d中最為關鍵的節點；反之，原始路網中排名第3的節點（編號84）在經過兩次攻擊后直接下降到第118位（圖2c），即成為剩余路網中不重要的節點.根據該例子可知，實際路網在遭受惡意攻擊后，介數中心性的變化非常大，原始路網中一些非常重要的節點在少數幾次攻擊后就可能變得不重要；而一些之前不重要的節點在剩余路網中會迅速變得很重要.因此，充分考慮路網在遭受攻擊后網絡節點或者邊的重要性變化，其路網抗毀性分析將更為科學、合理.

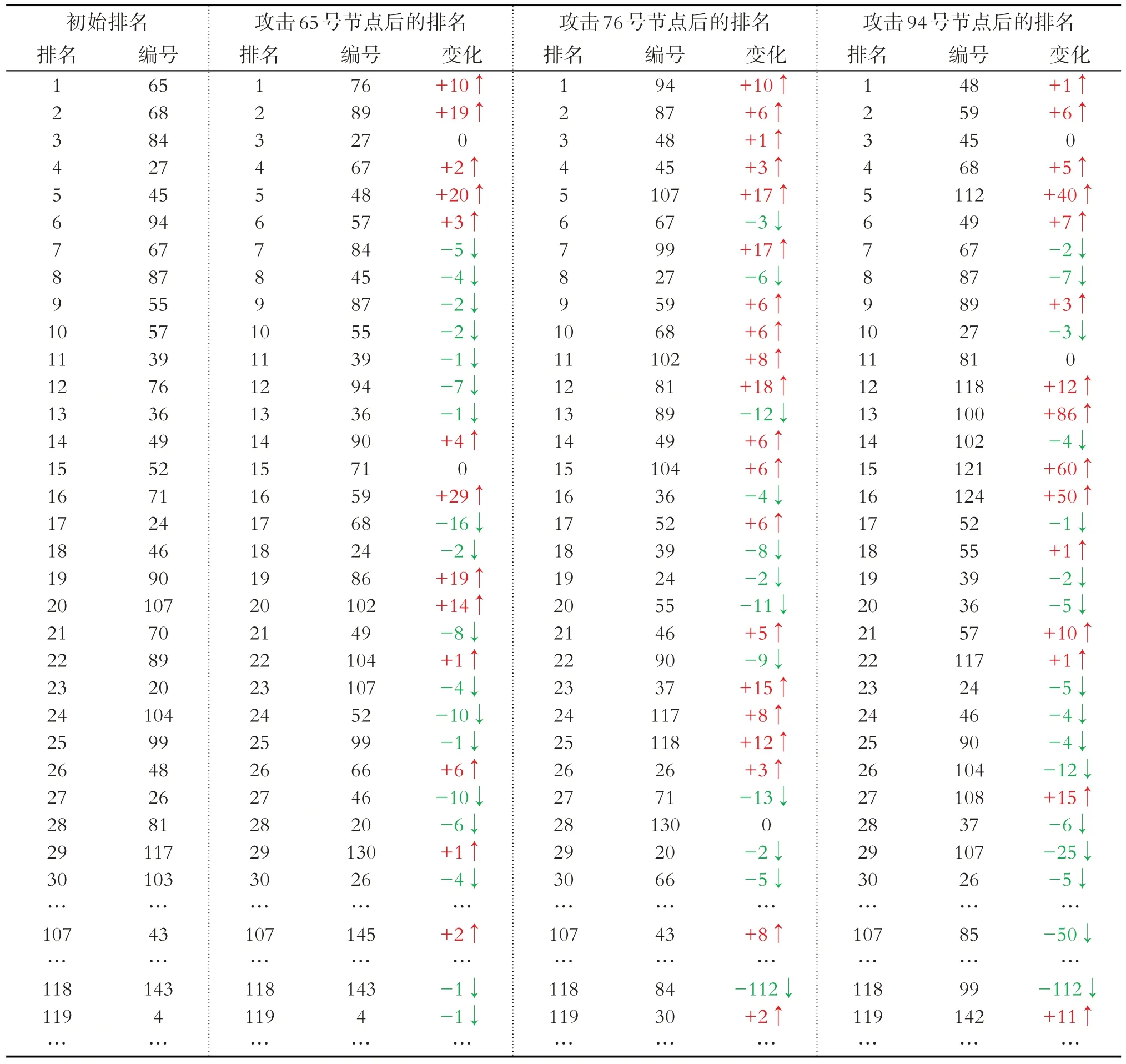
表1 動態介數優先的惡意攻擊方法下節點重要度變化（攻擊圖2路網節點）Table 1 Changes in the importance of nodes under the targeted attack method based on dynamic changes of betweenness centrality(attacking nodes in the road network in Fig.2)

2.2.2 算法描述

根據上述基本思想，本文提出一種基于動態介數中心性度量的公路網抗毀性評價方法.對于基于道路-道路關系的對偶圖和基于節點-節點關系的路網拓撲模型，都可以采用該算法進行抗毀性分析.以基于節點-節點關系的路網拓撲模型為例，抗毀性分析算法的具體過程描述如下：

（1）針對初始路網拓撲模型G=(V,E)，計算路網的整體效能指標E(G)；

（2）根據介數中心性方法計算當前路網中所有節點的介數中心性指標，進而按照介數大小對所有節點進行排序；

（3）攻擊當前路網中介數最大的節點vk，從網絡中移除該節點及其連接的所有邊，更新網絡拓撲結構G'=(V',E')；

（4）重新計算剩余路網的整體效能指標E(G')；

（5）回到步驟（2），直到攻擊完所有節點.

圖3所示為該算法的流程圖.在具體的抗毀性分析過程中，如果原始路網規模很大（比如上萬個節點），每次攻擊若只針對單個點或邊，效率會非常低.所以，一般可以采取按比重r攻擊，即按照路網規模的一定比例設施單次攻擊.這里，比重r的取值對結果有一定影響，r太大（如30%）不能反映路網效能的變化趨勢，r太小（如0.01%）計算量會很大.為準確刻畫路網整體效能與攻擊程度之間的關系，本文認為r取值在1%左右較為合適，這樣能在可控的計算規模下得到路網整體效能隨攻擊程度的連續變化.

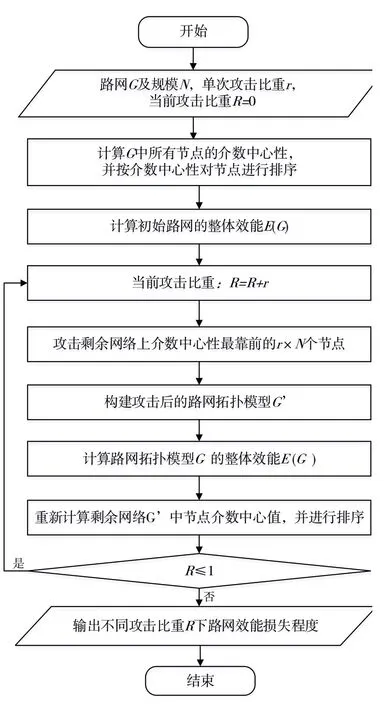
圖3 基于動態介數優化的路網抗毀性分析算法流程圖Fig.3 The flowchart chart of the algorithm with dynamic betweenness centrality priority

3 實驗與討論

3.1 實驗數據

以成都市道路網絡（圖4）為例，根據上述路網拓撲建模方法進行兩種網絡建模.基于道路-道路關系對偶拓撲模型共包含1484個節點（對應1484條道路）和5073條邊；基于節點-節點關系的路網拓撲模型共包含5162個節點和8943條邊（對應8943條路段）.本文將針對兩種路網拓撲模型進行實驗分析，并討論在不同攻擊策略下路網的抗毀性情況.

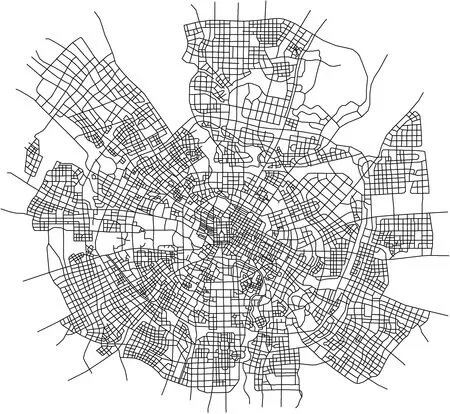
圖4 成都市城市道路網絡Fig.4 The road network of Chengdu

3.2 路網抗毀性分析場景設計

為系統分析公路網在不同攻擊下網絡整體效能的變化，針對基于節點-節點關系的路網拓撲模型，從攻擊方式（隨機、靜態或動態）、攻擊目標（節點或邊）角度設計了6種攻擊場景，具體如下：

（1）隨機攻擊節點策略.每次攻擊實驗均隨機選擇網絡上的節點，并計算在不同破壞程度下的網絡整體效能損失比例，進而分析路網效能損失比例與攻擊比重之間的關系.為保證隨機攻擊的準確性，進行100組隨機攻擊試驗，并計算每個攻擊比重下網絡整體效能損失比的平均值.

（2）隨機攻擊路段策略.即隨機攻擊網絡邊，計算在不同破壞程度下的網絡整體效能損失比例，分析路網效能損失比例與攻擊比重之間的關系.同樣，進行100組隨機攻擊試驗并取平均值.

（3）基于靜態介數優先的節點攻擊策略.根據初始路網計算所有節點的介數中心性，并按照介數從大到小進行節點攻擊，計算不同攻擊程度下路網的整體效能.該策略下，所有節點的介數中心性是靜態的.

（4）基于靜態介數優先的路段攻擊策略.根據初始路網計算所有路段的介數中心性，并對其進行排序，然后從中心性從高到低進行路段攻擊，計算路網整體效能的變化.

（5）基于動態介數優先的節點攻擊策略.該攻擊場景下，主要根據本文方法進行攻擊實驗，即每次攻擊后都需要重新計算所有節點的介數中心性，并以剩余路網中介數中心性最高的節點作為攻擊目標.

（6）基于動態介數優先的路段攻擊策略.即根據本文方法動態計算每次攻擊后路網上所有路段的介數中心性，確保下一次攻擊目標是剩余路網中最重要的路段.

針對基于道路-道路關系的路網拓撲模型，仍然從攻擊目標和攻擊方式角度采用上述6種攻擊策略進行公路網的抗毀性分析.因此，本文共設計了12種攻擊場景（表2）.

表2 公路網抗毀性分析攻擊場景設計Table 2 Scenarios of the attack experiment

3.3 結果與討論

3.3.1 基于道路-道路關系的路網拓撲模型抗毀性分析結果

針對成都市道路網絡的對偶拓撲模型，完成了上述6種場景下的抗毀性分析實驗（圖5、圖6）.結果表明：①無論是攻擊節點還是邊，隨機攻擊策略對路網整體效能影響最小，攻擊效果最差，而基于動態介數優先的惡意攻擊效果最好.以攻擊節點為例，當破壞比重為20%時，隨機攻擊下路網整體效能降低約為45%，靜態介數優先的惡意攻擊下路網整體效能降低約為70%，動態介數優先的惡意攻擊下路網整體效能降低超過90%.實驗結果證實了公路交通網絡面對隨機攻擊的魯棒性和面對惡意攻擊的脆弱性.②對于隨機、靜態和動態三種攻擊策略，攻擊節點比攻擊邊對路網整體效能的影響更為顯著.以動態介數優先攻擊為例，當攻擊比重為15%時，攻擊邊造成路網整體效能降低約36%，而攻擊節點將導致整個路網的效能損失約87%，這是由于在路網對偶圖中節點代表的是道路，攻擊一條主干道將破壞較多的連接關系，故造成的影響會很大.

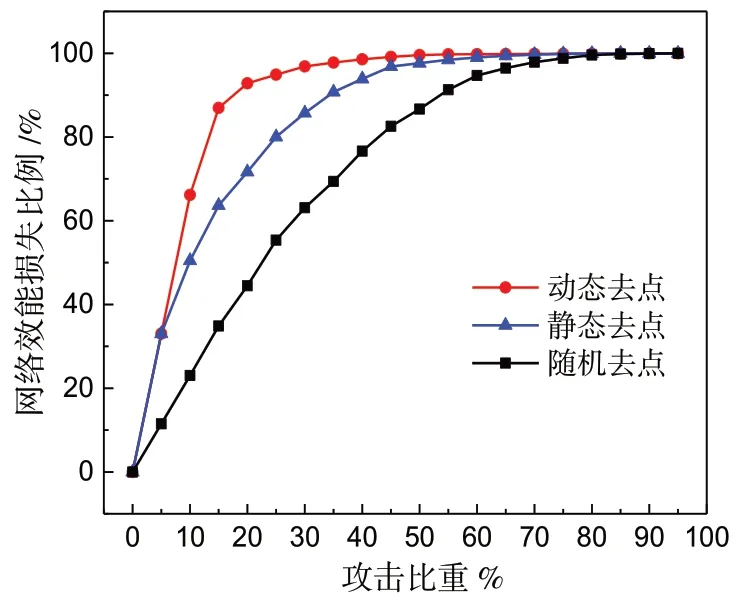
圖5 基于路網對偶圖的隨機和惡意去點攻擊對比Fig.5 Comparison of random attack and two targeted attacks on nodes based on the dual topological model of road network

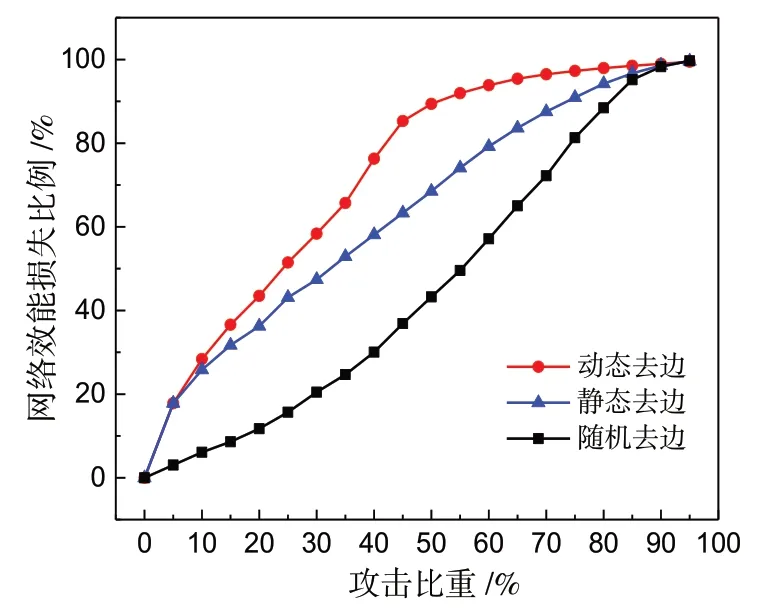
圖6 基于路網對偶圖的隨機和惡意去邊攻擊對比Fig.6 Comparison of random attack and two targeted attacks on edges based on the dual topological model of road network

可見，相比于傳統的靜態惡意攻擊策略，考慮路網動態中心性動態變化的惡意攻擊方式能達到更好的攻擊效果，其根據原因在于本文方法顧及了在攻擊過程中道路、節點或者路段的重要性的變化，能夠確保后續的惡意攻擊始終破壞的是當前路網中最為關鍵的部分.這為做好公路網安全防控提供了有力支撐.

3.3.2 基于節點-節點關系的路網拓撲模型抗毀性分析結果

利用本文方法，針對基于節點-節點關系的路網拓撲模型進行了抗毀性實驗分析（圖7、圖8）.與基于道路-道路關系的對偶網絡相比，該路網模型是對原始路網的精細表達，即每個路段（弧段）都有一條邊與之對應.所以，兩種路網模型的攻擊尺度（單次攻擊破壞程度）存在較大差異：對于道路級別的對偶圖，攻擊節點將破壞整條道路及其與鄰接道路之間的連接關系，攻擊邊將破壞兩條道路之間的連接關系；對于路段級別的網絡，攻擊節點只破壞該路口及與之連接的多個路段，攻擊邊只破壞單個路段（而包含該路段的道路上的其他路段不受影響）.基于節點-節點關系的路網模型抗毀性結果表明：①無論是攻擊節點還是路段，動態介數優先的惡意攻擊策略的攻擊效果最好；②對于三種策略，攻擊節點比攻擊路段能更快地破壞整個路網.當節點攻擊比重為15%，動態介數優先的惡意攻擊方式下路網效能損失達到80%以上，而靜態介數優先方式的破壞程度為65%，隨機攻擊方式的破壞程度不足40%.當邊攻擊比重為15%，動態介數優先方式下路網效能損失為55%，而靜態介數優先方式的破壞程度為35%，隨機攻擊方式的破壞程度為15%.

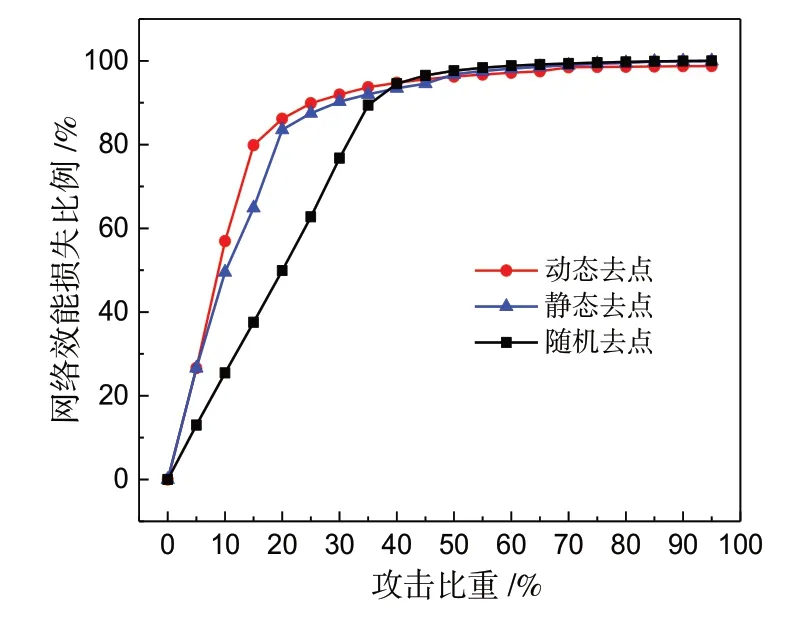
圖7 基于節點-節點關系的路網拓撲的隨機和惡意去點攻擊對比Fig.7 Comparison of random attack and two targeted attacks on nodes based on the node-node topological model

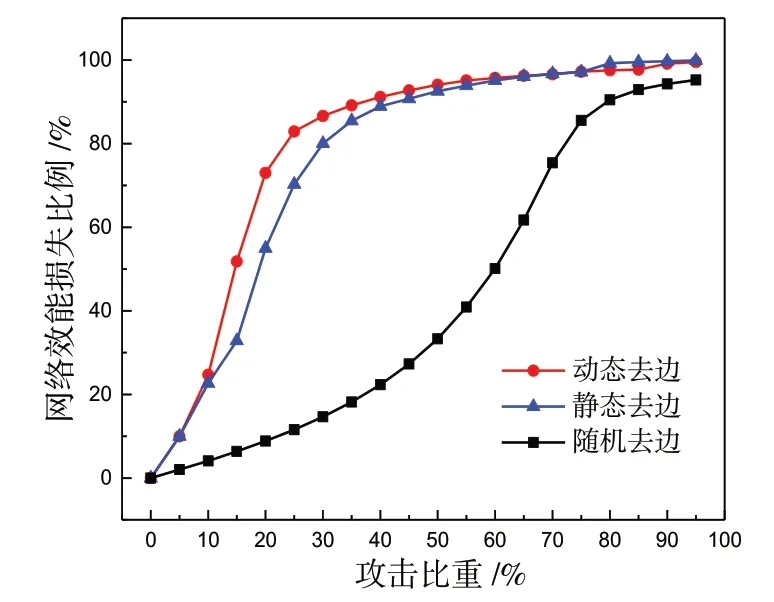
圖8 基于節點-節點關系的路網拓撲的隨機和惡意去邊攻擊對比Fig.8 Comparison of random attack and two targeted attacks on edges based on the node-node topological model

根據兩種路網模型的攻擊實驗可知：與隨機攻擊相比，惡意攻擊方式下路網整體效能降低更快；與靜態介數優先的惡意攻擊相比，基于動態介數優先的惡意攻擊方式能更快地破壞路網結構，攻擊效果最好.

3.3.3 討論

城市路網抗毀性分析有助于揭示路網在各種攻擊下的可靠性，挖掘攻擊各路段后對整個路網的影響，但如何合理地評價公路網的抗毀性是很重要的.面對隨機攻擊（無論攻擊節點還是邊），公路網表現出較強的魯棒性；反之，面對惡意攻擊，公路網則表現得非常脆弱.該現象是無標度網絡系統通常具有的特性.然而，如果要分析在給定破壞程度（網絡整體效能損失比）條件下最佳的攻擊策略，即具體破壞哪些關鍵道路且破壞道路數量盡可能少?隨機攻擊方式無法解決該問題.但基于網絡元素重要度變化的惡意攻擊是解決此類問題的一個優解，本文所提出的惡意攻擊方法體現了該思想，其抗毀性分析結果也表明該策略對路網整體效能破壞更快，攻擊效果比傳統惡意攻擊策略更為顯著.從兩種路網模型的抗毀性分析結果可知，在基于道路尺度的對偶圖中直接攻擊節點對路網造成的影響更大，本質上此時破壞的是一整條道路，從結構上該道路的損毀將破壞許多道路的連通關系，所以導致剩余路網中道路的中心性可能變化較大，這也是在路網對偶圖中實施動態介數優先惡意攻擊策略產生的影響尤為顯著的原因所在.該結論將為評估路網的魯棒性提供重要理論依據.

4 結語

城市路網抗毀性分析對整個城市交通系統的運行、城市安全以及理解城市功能具有重要意義.傳統方法主要從道路、路段或節點的靜態重要度角度進行抗毀性分析，然而在實際惡意攻擊中路網上各要素的重要度會變化，導致后續攻擊目標可能并非是當前網絡中最為重要的.針對該問題，本文提出一種基于動態介數中心性優先的城市抗毀性分析方法.該方法通過動態計算路網在遭受攻擊后的中介中心值，重新評估各節點和道路在剩余路網中的重要性，為后續攻擊提供了依據.為檢驗該方法的有效性，以實際城市路網為例，分別針對基于道路-道路關系的對偶拓撲模型和基于節點-節點關系的路段網絡模型進行面向隨機攻擊、靜態介數優先的惡意攻擊和動態介數優先的惡意攻擊試驗.結果表明，對于兩種路網拓撲，無論是攻擊節點還是邊，動態介數優先的惡意攻擊策略表現出更好的攻擊效果.該方法為進一步揭示城市路網功能及識別關鍵道路提供了新的研究思路.