函數思想在物理強基試題中的應用
王朝祥
(北京市第八十中學)
基礎學科招生改革試點也稱強基計劃,主要是為了選拔培養有志于服務國家重大戰略需求且綜合素質優秀或基礎學科拔尖的學生.從考查內容和能力要求來看,強基試題延續了自主招生試題的特點,并進一步突出對學生數學、物理等基礎學科的考查,要求學生能運用數學思想方法分析解決物理問題.
函數描述一個量隨其他量的變化關系,變量是函數的基礎,對應(映射)是函數的本質.函數思想的應用是指用函數的概念和性質分析問題、轉化問題和解決問題.普遍聯系和運動變化的觀點是函數思想的精髓.高中物理常用的函數有一次函數、二次函數、冪函數、指數函數、對數函數、三角函數,涉及函數的定義域、值域、單調性、奇偶性、周期性、極值等問題.實際應用中,不等式、數列、導數、定積分等問題也屬于函數范疇.本文重點討論函數思想在強基試題中的應用,闡述利用函數思想解決問題的一般思路.
1 利用導數思想,拓展解決問題的思路
函數y=f(x)在x=x0處的瞬時變化率,稱為函數在該點的導數,記作f′(x0),即
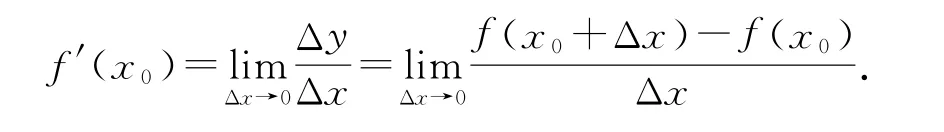
導數f′(x0)反映函數y=f(x)在x=x0處的增減趨勢和變化快慢.在圖像中,導數f′(x0)的幾何意義為曲線y=f(x)在x=x0處切線的斜率.
高中物理中,很多物理量都是通過變化率定義的,例如,速度是位移對時間的變化率,加速度是速度對時間的變化率,力是動量對時間的變化率,功率是能量對時間的變化率,感應電動勢是磁通量對時間的變化率.導數是函數對自變量的瞬時變化率,將導數思想引入物理實際問題,能有效拓寬學生的思路,并能化解僅用初等數學知識難以解決的問題,提升學生運用數學工具處理物理問題的能力.現結合一些常見問題舉例說明.
例1 (2011年華約自招)如圖1所示,紙面內兩根足夠長的細桿ab、cd都穿過小環M,桿ab兩端固定,桿cd可以在紙面內繞過d點并與紙面垂直的定軸轉動.若細桿cd從圖示位置開始,按照圖中箭頭所示方向,以勻角速度轉動,則小環M的加速度( ).

圖1
A.逐漸增加
B.逐漸減小
C.先增加后減小
D.先減小后增加

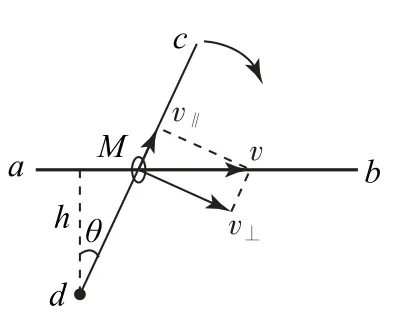
圖2
例2 (2015年清華領軍計劃)在距離水面高度為h的岸上,有人用繩子經定滑輪拉著小船靠岸,人收繩子的速率恒為v0,當小船與岸邊的水平距離為s時,其速度、加速度分別多大?


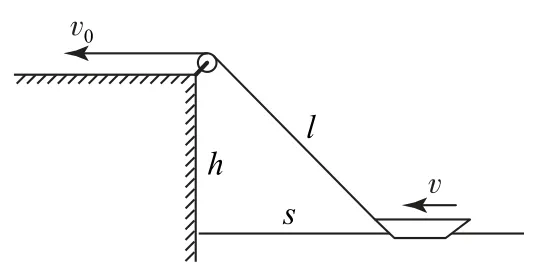
圖3

2 利用定積分化解連續函數求和問題
定積分的本質是連續函數的求和,其在高中物理中的應用涉及速度或位移的計算、液體壓力的計算、變力做功問題、物理量的平均值問題、轉動慣量問題、連續帶電體電勢的計算、交流電有效值的計算等.在物理教學中適當滲透定積分“分割—建立微元—求和”的思想方法,有助于學生對物理概念的準確理解和辨析,進而提升學生運用數學知識處理物理問題的能力,拓展思維空間.

例3 (2017年北大綜合營)一盛水的容器繞豎直中心軸勻速轉動,求容器內水面形狀.

如圖4所示,取旋轉液面表面任意位置(x,y)處的小水珠,質量記為m,該處液面切線與水平方向夾角記為θ.在旋轉的非慣性系中分析水珠受力,考慮慣性力,三力平衡,且有
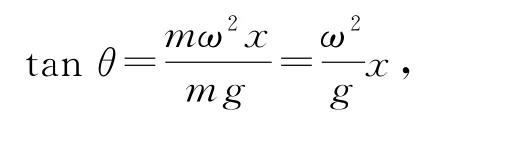

圖4

3 函數思想在極值問題中的應用
分析物理中的極值問題常涉及代數、幾何、向量、微積分等多個數學分支,對學生的分析綜合能力和應用數學知識解決物理問題的能力要求較高.解決極值問題的一般思路是認真分析物理情境,根據物理中的定理或定律建立因變量與自變量之間的函數關系,再利用數學方法求極值.在上述過程中,函數構建是解決問題的關鍵.
例6 一均勻細桿置于粗糙地面上,人對其一端施力,力與桿始終垂直,要將桿無滑動地慢慢抬到豎直位置,則桿與地面之間的靜摩擦因數至少應該多大?

如圖5所示,對桿受力分析,列共點力平衡方程有Fcosα+FN=mg,Fsinα=Ff,以A點為軸,由轉動平衡有


圖5

若n個數x1、x2、x3、…、xn的和為定值,當這n個數都相等時,它們的積有最大值;若n個數x1、x2、x3、…、xn的積為定值,當這n個數都相等時,它們的和有最小值.
例7 (2013年華約自招)明理同學平時注意鍛煉身體,力量很大,最多能提起m=50kg的物體.一重物放置在傾角θ=15°的粗糙斜面上,重物與斜面間


如圖6 所示,設該同學拉動重物的力F的方向與斜面成角度α,根據力的平衡,若重物剛好能被拉動(a=0),在垂直于斜面方向有
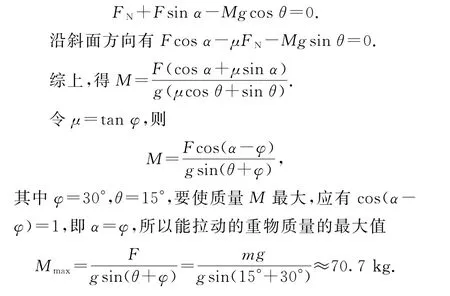

圖6

本題考查共點力的平衡,要求學生能熟練列出力的平衡方程,并能運用三角函數知識求極值,對數學運算能力要求較高.
若引入摩擦角和全反力的概念,本題可以采用矢量圖解法分析,解題思路大為簡化.
如圖7所示,斜面對重物的支持力FN與最大靜摩擦力Ffm的合力稱為全反力R,全反力與支持力的夾角φ稱為摩擦角,tanφ=μ,用R等效代替FN與Ffm,本題轉化為三力平衡問題.
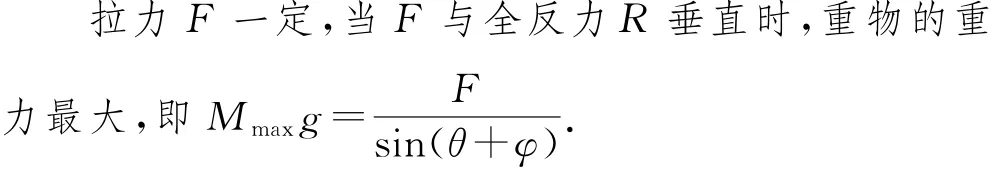
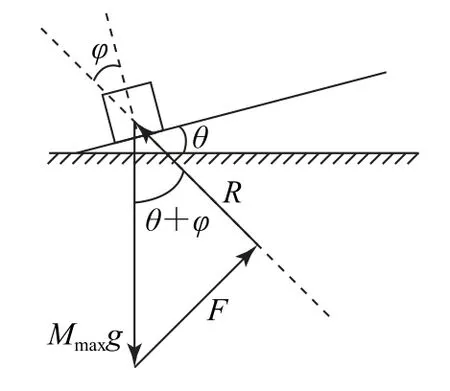
圖7
綜上所述,函數思想在強基試題中有廣泛的應用.利用函數思想解決物理實際問題的一般思路如下:1)根據物理情境梳理相關物理量之間的函數關系,從而把物理模型轉化為數學模型;2)經過數學演算、推理得出結果;3)再結合物理情境討論數學結果的物理意義,得出符合實際的結論.在上述環節中,函數構建是解決問題的關鍵.

