聯合三階Keystone變換與相關函數的機動目標補償算法
郭曉樂, 武正翔, 王善松, 張 科, 楊雪亞
(1. 中國電子科技集團公司第三十八研究所, 安徽合肥 230088; 2. 孔徑陣列與空間探測安徽省重點實驗室, 安徽合肥 230088; 3. 中國人民解放軍63629部隊, 北京 102600)
0 引 言
隨著武器裝備的不斷更新發展以及新型吸波材料的應用,戰斗機、導彈等空中目標的有效截面積越來越小,反射系數越來越低,信噪比越來越小。對于傳統的機載脈沖多普勒(Pulse Doppler, PD)雷達而言,通過多個脈沖進行相參積累從而提高目標信噪比,達到從噪聲中檢測出目標的目的[1-3],對于信噪比很低的弱目標,PD雷達為了能夠提高檢測的信噪比,需要不斷增加相參積累的時間,但是當積累時間增大時,由于目標的高速高機動會引起多個脈沖跨越多個雷達的距離分辨單元[4-6],導致相參積累的能量分散到多個距離單元,此外,目標回波的高階相位項還會導致多普勒的頻率走動,導致目標回波能量在多普勒頻道上出現散焦的現象,距離單元的走動和多普勒散焦的現象都會降低機載PD雷達的檢測性能。現有的基于目標速度的包絡補償算法需要準確知道目標的速度來對接收脈沖串進行脈間和脈內的補償;而普通的Keystone變換方法[7-11]雖然不用準確已知目標速度,可以對目標速度進行估計,但是這種方法只能補償目標速度導致的距離走動,而忽略了高機動目標的高階運動參數對相參積累的影響,因此只適用于低機動目標檢測或短時間積累的場合;廣義拉東-傅里葉變換[12](GRFT)和拉東多項式-傅里葉變換[13](PRPFT)等算法雖然可以實現對目標各階距離走動的消除和相位的補償,但是都需要對目標參數進行多維度搜索,運算量比較大,非常不適用于工程實現。
針對高機動目標的運動補償問題,本文提出了一種基于聯合三階Keystone變換、相關函數與尺度變換的距離維和多普勒維走動校正方法。首先對接收信號進行傳統的脈壓處理,然后通過對慢時間進行三階Keystone變換處理,消除由目標加加速度導致的距離走動,接著對三階Keystone變換結果分別進行頻移后,將兩個信號進行共軛相乘并進行距離維的IFFT處理,緊接著構造自相關函數,進行慢時間變量的相參積累,到這里可以補償掉機動目標引起的所有距離走動現象;之后對自相關函數的慢時間變量進行尺度變換,并對尺度變換后的信號針對時延和慢時間進行二維FFT變換,從而消除掉目標的多普勒散焦現象,得到目標聚焦峰值點,順利地進行目標檢測。
1 高機動目標回波模型
對于PD雷達而言,雷達發射的基帶信號為線性調頻信號(LFM),信號模型可以表示為
(1)
式中,t為單個脈沖持續的時間,即快時間,T0為發射脈沖寬度,fc為雷達載波頻率,K為線性調頻信號的調頻斜率,t為脈內快時間,矩形窗函數定義為
(2)
假設PD雷達發射的脈沖數為M,脈沖重復間隔為Tr,則脈間的慢時間序列可以表示為tm=mTr(m=0,1,…,M-1)。假設一個相對雷達做高機動運動的目標,初始距離、徑向速度、加速度和加加速度分別表示為R0,c1,c2和c3,則高機動目標相對于雷達在tm時刻的瞬時距離可以表示為
(3)
經數字解調后,接收回波信號數據的基帶信號可以表示為
(4)
式中,Ar為回波信號的幅度,c表示光速,λ=c/fc表示雷達波長。
對上述的基帶回波信號進行距離維脈沖壓縮,可得脈壓后的回波信號為
(5)
式中,Ac為脈沖壓縮后回波信號的幅度,B=KT0表示雷達信號帶寬。
在PD雷達中,一般情況下,目標具有多普勒模糊,即目標的速度表示為
c1=c0+Nambvamb
(6)
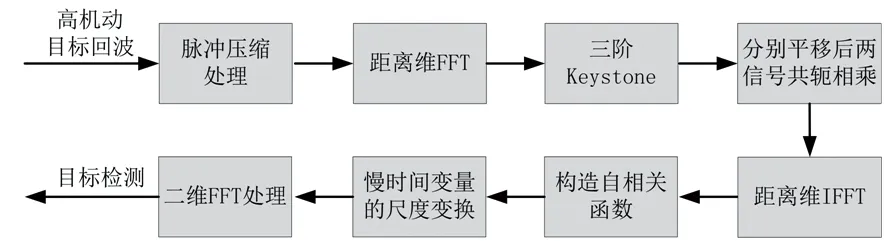
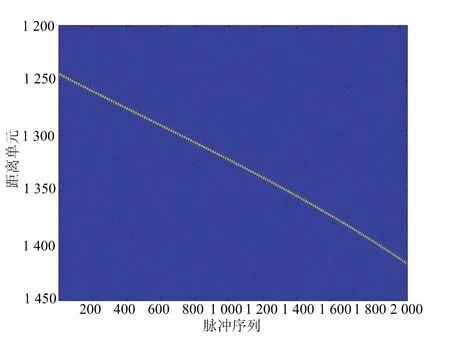
式中,Namb為多普勒模糊次數,vamb=λ/(2Tr)為雷達的最大不模糊速度(盲速),c0=mod(c1,vamb)為目標的基帶速度,滿足|c0| 將式(3)和式(6)代入式(5),式(5)中脈壓后的回波信號可以表示為 (7) 式中: (8) 由此可以看出,脈壓后的回波信號可以簡化為 (9) 由上式可以看出,脈壓回波在快時間維的sinc函數包絡位置隨著慢時間tm的變化而變化,并且慢時間維的高階相位項會導致多普勒譜發生展寬。當雷達進行長時間積累時,目標的能量在距離維和多普勒維都會產生跨單元走動的現象,這樣會嚴重影響目標的檢測。 對式(9)進行距離維的FFT,可得 (10) 式中,f為t對應的距離頻率分量,Af表示傅里葉變換后的雷達信號幅度。 由式(9)和式(10)可以看出,目標在距離維和多普勒維產生的單元走動現象是距離頻率變化量f與慢時間變量tm之間存在耦合反應到快時間維的結果所致,因此要校正距離維和多普勒維產生的單元走動現象,就需要消除距離頻率變化量f與慢時間變量tm之間的耦合關系。 針對高速運動目標,Keystone變換被提出并廣泛的應用,Keystone變換實際上是通過對慢時間軸進行尺度變換來消除距離頻率變化量f與慢時間變量tm之間的耦合,從而校正目標的距離走動,對式(10)中的慢時間tm通過下式替換: (11) 式中,tn可以表示為虛擬的慢時間變量。 Keystone變換可以認為是一個慢時間維的信號重采樣過程,將式(11)代入式(10)可得 (12) 針對窄帶雷達環境(f遠小于fc)而言,將上式關于f進行一階泰勒展開,可得 (13) 由式可以看出,經過了Keystone變換后,目標的基帶速度引起的距離走動得到了有效消除。然而,上式中距離頻率f和慢時間tn之間仍然存在耦合現象,說明Keystone變換只能校正目標基帶速度導致的距離走動,然而目標的高階運動參數和多普勒模糊導致的走動仍然沒有被有效校正。 由于目標的加加速度c3會導致距離彎曲現象,本文引入三階Keystone變換的,變換的關系如下: (14) 將式(14)代入式(10),并關于f進行一階泰勒展開,可得 (15) 由上式可以看出三階Keystone變換消除了由目標加加速度導致的距離走動現象,而由于目標速度和加速度導致的距離走動有剩余。接下來開始消除這兩項的距離走動現象,本文構造式(15)信號的相關函數為 (16) 上式中定義的相關函數實際上是對三階Keystone變換結果分別進行頻移后,再將兩個信號進行共軛相乘的過程,緊接著對Sc2(tn,f)進行距離維的IFFT處理,可以得到 (17) 式中,Ac2表示IFFT后信號幅值。 式(17)可以看出,經過相關處理后,機動目標的能量集中到同一個距離單元,距離走動得到了有效消除,并且慢時間維的三階相位項也得到了消除,針對式(17)中的慢時間變量可以重新建模為一個LFM,如下: (18) 式中,A=Ac2exp(-j2πBR0/c)表示幅值,f0=-B(2c0/3+Nambvamb)/c為等效載頻,K0=-2Bc2/(3c)為等效調頻斜率。經過上述所有的處理,可以說所有脈沖的脈內脈壓都壓到了同一距離單元,緊接著看是進行脈間的相參積累。 針對式(18)慢時間變量進行相參積累,本文通過自相關處理實現[14]。構造以下的自相關函數為 A2exp[j2πf0(τ+a)+j2πK0· (τ+a)tn] (19) 式中,τ為一個時延變量,a為一個固定的時延。 從式(19)可以看出經過自相關處理后,tn和τ之間出現了耦合現象,這會導致該自相關函數的二維頻譜也出現跨單元走動的問題,緊接著開始解決這一問題,本文定義如下的尺度變換: (20) 式中,h表示一個尺度因子,是一個常量。 將式(20)代入式(19),可得 (21) Affexp(j2πfτ)sinc(fτ- (22) 根據式(22)可以看出,經過二維FFT處理后,目標的能量會聚焦為一個譜峰,此峰值可以進行目標檢測。 本小節對所提方法的運算復雜度進行分析。假設Nr和M分別表示雷達回波的距離單元個數和脈沖個數。本文方法首先利用三階Keystone變換進行部分的距離校正,所需的運算復雜度為O(MNrlog10(M));緊接著頻移互相關處理和距離維的IFFT處理所需的運算復雜度為O(MNrlog10(Nr)),最后,尺度變換后對慢時間維的二維FFT變換需要的惡運算復雜度為O(M2log10(M))。綜上所述,本文所提方法的總的運算復雜度為O(MNrlog10(M)+MNrlog10(Nr)+M2log10(M))。 GRFT和PRPFT都是基于全參數搜索的算法,需要對目標初始距離和目標運動參數進行四維搜索,假設NRs、Nc1s、Nc2s和Nc3s分別表示目標初始距離、徑向速度、加速度和加加速度的搜索次數,則這兩種方法需要的運算復雜度為O(MNRsNc1sNc2sNc3s)。如果假設M=Nr=NRs=Nc1s=Nc2s=Nc3s=N,則本文方法的運算復雜度約為O(N2log10(N))量級,而GRFT和PRPFT的運算復雜度約為O(N5)量級,由此可知,本文所提方法運算量遠小于GRFT和PRPFT這兩種方法。 綜合前面的所有分析,聯合三階Keystone變換、相關函數與尺度變換的距離走動和多普勒走動補償處理的流程有: 1) 高機動目標回波數據進行脈沖壓縮處理,得到脈壓回波數據; 2) 距離維的FFT,得到距離頻率變化量f與慢時間變量tm之間的耦合關系; 3) 對慢時間進行三階Keystone變換處理,消除由目標加加速度導致的距離走動; 4) 對三階Keystone變換結果分別進行頻移后,將兩個信號進行共軛相乘; 5) 進行距離維的IFFT處理; 6) 構造自相關函數,進行慢時間變量的相參積累; 7) 對自相關函數的慢時間變量進行尺度變換; 8) 對尺度變換后的信號針對時延和慢時間進行二維FFT變換,得到目標聚焦峰值點。 處理流程如圖1所示。 圖1 聯合三階Keystone變換、相關函數與尺度變換的距離走動和多普勒走動補償流程圖 為了驗證本文方法的有效性,進行一個典型參數的仿真實驗來驗證本文方法的有效性,表1給出了雷達系統的仿真參數。 根據表1中所列的仿真參數,對高機動目標進行仿真處理。圖2給出了仿真參數下,高機動目標回波的脈壓結果,由圖可知,目標的高機動運動導致嚴重的距離走動,距離走動了164個距離單元。緊接著對回波信號進行三階Keystone變換處理,消除由目標加加速度導致的距離走動,之后 Keystone變換結果分別進行頻移后,將兩個信號進行共軛相乘,進行距離維的IFFT處理,并構造自相關函數處理,得到慢時間變量的相參積累,圖3給出了聯合三階Keystone變換與相關函數的距離走動補償后歸一化能量圖,由圖可知,經過處理后雖然目標的距離走動被補償掉了,但是在多普勒頻道上面出現了散焦。緊接著進行流程中的7)、8)兩步,得到圖4所示的慢時間尺度變換后二維FFT處理結果,從圖可見目標能量在二維平面上積累為一個譜峰,可以準確地實現目標檢測。 表1 雷達系統的仿真參數 圖2 所有脈沖序列接收回波脈沖壓縮結果 圖3 聯合三階Keystone變換與相關函數的距離走動補償后歸一化能量圖 圖4 慢時間尺度變換后二維FFT處理結果 由于目標的高速高機動會引起相參積累的能量分散到多個距離單元,并且目標回波的高階相位項還會導致多普勒的頻率走動,導致目標回波能量在多普勒頻道上出現散焦的現象,距離單元的走動和多普勒散焦的現象都會降低機載PD雷達的檢測性能。針對高速高機動目標的運動補償問題,本文提出了一種基于聯合三階Keystone變換、相關函數與尺度變換的距離維和多普勒維走動校正方法。通過三階Keystone變換和構造的自相關函數補償掉機動目標引起的所有距離走動現象,并且通過慢時間變量的尺度變換來消除多普勒的散焦現象,最后得到目標聚焦峰值點。仿真實驗驗證了方法的有效性。


2 傳統的Keystone變換進行走動補償
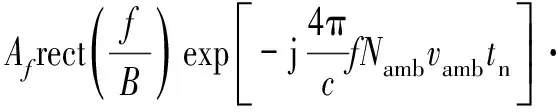
3 聯合三階Keystone變換、相關函數與尺度變換的距離維和多普勒維走動校正
3.1 距離走動校正
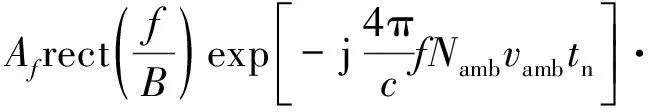
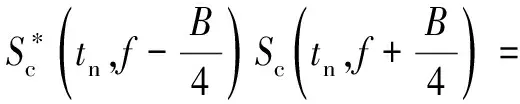
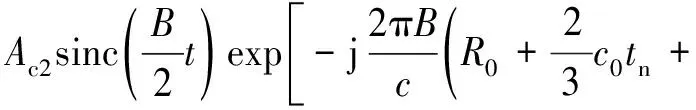
3.2 多普勒頻率走動校正



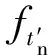
3.3 運算復雜度分析
4 處理流程及仿真實驗



5 結束語

