打破思維定式,落實核心素養
張亞光
(太和縣馬集鎮中心小學 安徽阜陽 236638)
小學生掌握的數學知識較少,再加上邏輯思維能力比較薄弱,他們對新知的獲取往往建立在模仿的基礎之上。“數學是一門關于模式和秩序的學科”,在新知識的理解和運用上,小學生常因思維定式而犯錯。要規避這種錯誤,引導學生向著思維定式的正方向發展,就要對思維定式有著更理性的認識。
一、思維定式的界定
認知心理學認為,由一定的心理活動所形成的準備狀態對于問題的解決起到促進或妨礙的作用,這種狀態叫作思維定式。可見,思維定式有其積極的一面,也有其消極的一面。作為教師,要運用恰當的教學手段引導學生朝著符合數學思維的方向發展,朝著思維定式積極的一面發展,使知識產生正遷移。
二、思維定式產生的原因分析
(一)正負遷移
問題1:簡便運算25×125×32=
生1:25×125×32=25×125×(4×8)=(25×4)×(125×8)=…
生2:25×125×32=25×125×(4×8)=(25×4)+(125×8)=…
生1對乘法結合律非常熟悉,并且知道25和4常結合,125和8常結合,進而想到把32分成4×8,這是對乘法結合律的運用熟練到一定程度的結果,也是思維定式積極的一面。有了上述思維定式,便能很快地解答本題,此為知識技能的正遷移。
生2在運算時,看到兩頭乘,聯想到乘法分配律。把乘法分配律負遷移到這里,是很多學生經常犯的錯誤。這主要是由于對乘法分配律的本質沒有理解透,故而將乘法分配律和乘法結合律混淆。對于某些新知識,理解不透徹而產生知識運用上的干擾,此為知識技能的負遷移。
問題2: 脫式計算 35+65×40÷5
在四年級學習混合運算時,學生易犯先算加法的錯誤,如下面生3的做法。出錯原因一方面是學生對“從左到右計算”和“先乘除,后加減”這兩者的認知出現沖突,另一方面是對運算順序理解不到位。
生3: 35+65×40÷5 生4: 35+65×40÷5
=100×40÷5 =35+260÷5
筆者認為更重要的原因是一年級就學習了加減法計算,學生已經習慣從左到右的計算順序,在實際計算時,不知不覺又這樣做,導致“從左到右”的計算法則在這里發生負遷移。
(二)經驗主義
問題3:解方程5+3x=6
生5:5+3x=6,3x=1,x=3
生6:5+3x=6,3x=1,x≈0.33
生5在第二步系數化為1的時候,本該運用積除以一個因數,卻因“習慣”了大數除以小數,結果用3除以1。之前的學習經驗在這里產生了知識負遷移,導致出錯。
生6在最后結果處取近似數,其原因是在低年級學除法時,沒學分數,結果除不盡時就保留。基于這一經驗,生4在學了分數后,沒有形成用分數表示結果的習慣,結果還是取近似數。
可見,學生在舊知識較熟練,而新知識還不熟練時,會因思維定式產生知識負遷移。之前學習積累的經驗反而成了學生解題的“絆腳石”。
問題4:爸爸今年31歲,比兒子的年齡2倍還多5歲,兒子今年多少歲?
對于這個問題,很多學生把算式錯寫成(31+5)÷2,其原因是在一年級時,習慣了見“多”就加,見“少”就減。學生不能從本質上理解爸爸和兒子年齡的數量關系,而是憑經驗列式計算。教師往往利用線段圖,或者結合方程解法讓學生比較、辨析來糾正錯誤。在這個過程中,要讓學生體驗到經驗不是什么時候都能用得上的,只有科學、正確地分析數量關系,才能找到正確做法。
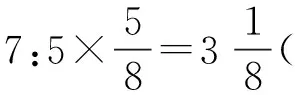
答:一個星期修不完。
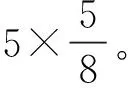
(三)審題不清
問題6:鐘表上,從12點到1點,分針轉了度。
本題常有學生錯填“30”這個答案,原因是審題時沒注意“分針”二字,思考時只想著12點到1點中間會有多少格、轉了多少度等。
問題7:一個長方體長、寬、高都擴大2倍,體積會( )。
A.擴大4倍 B.擴大6倍 C.擴大8倍
五年級學生在做這個題目時,常錯選B項,長、寬、高都擴大2倍,就是23,但是小學生對乘方計算還不熟練,把它當成了2×3來算。
三、打破思維定式的幾點建議
(一)強化解題技能
魏書生老師說過,學習就是“發展、發展、再發展,生長、生長、再生長”。要強化學生正確的、積極的一面,以此來“對付”學生易錯、易混的地方。這種教學思想,也可以用在糾正學生“思維定式負遷移”上面。數學是一門技能性學科,對于正確的技能,要達到熟練的程度才不會被“定勢”干擾。學生在學習了新知識后,若沒有做足夠的題進行強化、形成技能,很容易產生知識的負遷移。如對于問題3,學生在學習了“因數=積÷另一個因數”這個知識點后,只有做題強化、定時復習,才會避免因“定式”而出錯。只有對基本知識、基本技能的掌握達到一定熟練程度,才會產生思維定式的正遷移,避免思維定式的負遷移。在初學混合運算時,學生容易出現計算順序錯誤,而這種錯誤在后期很少出現,是因為學生經過了大量的練習、糾錯,熟練掌握了解題技能,理解了知識的本質。理解并掌握某一新知識,要有一個過程。在初學混合計算時,我們可以讓學生先觀察運算順序再算。熟練掌握基本技能,是避免出現思維負遷移的一個有效措施。
(二)重視思維過程
課堂上,我們不僅要關注學生的學習結果,更要關注學生在學習中的思維過程。小學生的學習以形象具體思維為主,他們的學習往往不深入,需要我們老師不斷鼓勵、引導他們走向深入。小學生的數學語言很匱乏,我們常發現學生會做題,卻說不出為什么這樣做。這就要教師重視知識的產生過程,從本源抓起。如問題1,若對乘法分配律有透徹的認識,學生就不會寫成25×4+125×8。
下面是筆者執教的一個教學片段。
師:你為什么把25×125×(4×8)這一步,寫成25×4+125×8呢?
生8:因為我想25和4結合,125和8結合,就想到了乘法分配律,所以就這樣做了。
師:乘法分配律用字母怎么表示呢?
生9:記不清了,好像式子兩頭乘法,中間加法。
生10:乘法分配律用字母表示是 (a+b)×c=a×c+b×c
師:這個式子左右兩邊各有什么特征呢?
生11:等式左邊是兩個數的和與一個數相乘的形式,右邊是兩個數分別與同一個數相乘,然后中間相加。
師:觀察得很仔細,只有兩個數的和或差與一個數相乘,才能變成“兩頭乘,中間加(或減)”的形式。而像25×125×(4×8)不可以變成25×4+125×8的形式,中間的加要改成乘才對。
作為一線教師,要站穩課堂,既要重視學習結果,又要重視學習過程。要在過程中,及時地反饋、評價,以此來促成好結果。
(三)培養學習習慣
要提高學生的思維品質,就要從培養學生的學習習慣抓起。教學時數學教師應該以嚴謹、認真的態度影響學生,小學生接受新知識的速度往往比較慢,幫學生打開思維、深入學習,比匆忙完成教學任務更重要。教育家杜威說過,“許多兒童由于緩慢,由于不能迅速作出回答而受到指責,其實,他們那時正在花費時間積聚力量以便有效處理他們面臨的問題。在這種場合下,若不能留給他們時間和空間,那就是鼓勵他們養成迅速的但卻是倉促的淺薄的習慣”。我們教師要學會等一等,引導學生走向深入學習。因思維定式產生知識的負遷移,往往是數學學習過程中不細致、不嚴謹的結果。像問題5,細致的學生是能注意到“分針”二字的,犯錯往往是因為不熟練、不細致,顧此失彼。數學是嚴謹的,我們要從平時抓起,從每一次數學思考抓起,培養良好的學習習慣。
(四)注重求異訓練
A.第一根長 B.第二根長 C.無法確定
A.剪去的繩子長
B.剩下的繩子長
C.無法確定
這兩題學生經常混淆,為此,筆者專門組織學生進行一次討論。
生12:問題8中“繩子總長不知道”,因此選“無法確定”,那問題9中“繩子總長不知道”,為什么就可以確定誰長呢?
師:問題8中是兩根繩子,問題9中是一根繩子。
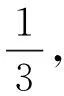
師:非常好,問題9中繩子長實際是一定的。不能一見到分數就以為它是分率,帶單位的分數它就表示一個量。
俄國著名教育家烏申斯基說,“比較是一切理解和思維的基礎,我們正是通過比較來了解世界上的一切”。比較是學生學習數學的一個重要方法,要針對學生產生負遷移的地方,專門設計一些練習,讓學生在比較后,進行充分的討論、辨析,從而糾正錯誤的“定勢”,形成知識的正遷移,最終實現正確的認知。小學生的思維常帶有不深入、停留在表面等特點,因此我們要引導學生觀察、比較、辨析。通過這些活動來提升學生的認識,加深學生對知識本質的理解,使學生思維走向深入。
四、結語
要避免思維定式產生負遷移,就要研究學生的“學”。只有充分了解學生,才能教好學生,才能使我們的教學目的明確、有效。我們只有把握學生的學習情況,引導他們朝著正確的方向發展,才能使學生避免因思維定式而產生知識負遷移。波蘭數學教育家波利亞說過,“教師教什么,當然是重要的,但是學生心里想什么,想知道什么卻是更重要的”。教師的教要建立在學生學的基礎之上。教學中要認真對待學生所犯的每一個錯誤,利用好這一生成性資源。對于思維定式引發的錯誤,要讓學生學會突破。只有更理性、更科學地處理學生因思維定式引發的錯誤,才能夠因學定教,才能真正落實核心素養。

