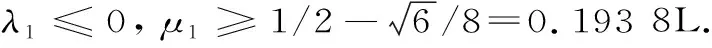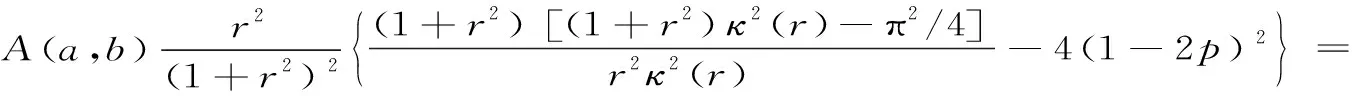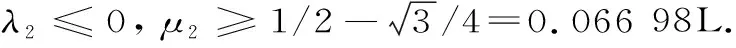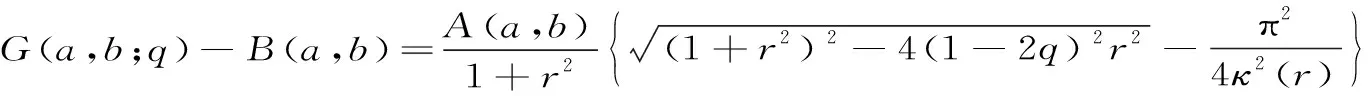特殊擬算術平均的單參數(shù)調和與幾何平均確界
楊 月 英
(湖州職業(yè)技術學院 機電與汽車工程學院, 浙江 湖州 313099))
一、研究基礎
設q∈[0,1],r∈和a,b>0且a≠b,則單參數(shù)對稱二元平均M(a,b;q),r階冪平均Mr(a,b),調和平均H(a,b),幾何平均G(a,b)和算術平均A(a,b)分別定義為:
M(a,b;q)=M[qa+(1-q)b,qb+(1-q)a].
(1)
(2)
我們熟知,對固定的a,b>0且a≠b冪平均Mr(a,b)關于r∈是連續(xù)且嚴格單調增加的,則會有不等式鏈
H(a,b)=M-1(a,b) 對所有的a,b>0且a≠b成立,其中L(a,b)=(a-b)/(lna-lnb)是對數(shù)平均. 1998年,Toader介紹了一個關于兩個正數(shù)a和b的經(jīng)典擬算術平均[1]358-368: 其中,rn(θ)=(ancos2θ+bnsin2θ)1/n(n≠0),r0(θ)=acos2θbsin2θ,p是一個嚴格單調增加函數(shù).許多特殊積分平均都是Mp,n(a,b)的特殊情形,例如: . 分別是Toader-Qi平均TQ(a,b),算術-幾何平均AG(a,b),Toader平均T(a,b),E(a,b)則是一個特殊的積分平均[2]1-10. 且可以寫為: (3) 關于完全橢圓積分在物理學,工程學,幾何函數(shù)理論,平均值理論,數(shù)論和其他相關領域有許多重要應用.在特殊情形下,若干含有完全橢圓積分的二元平均與其它二元平均的比較得到了許多數(shù)學工作者的深入研究[4]77-79 [5]637-642 [6]719-728 [7]1-12 [8]821-841.例如,楊月英證明了雙向不等式 和 H(a,b) (4) 對所有a,b>0且a≠b[3]42-46. 對p∈[0,1/2],我們不難證明單參數(shù)平均H(a,b;p)和G(a,b;p)對固定的a,b>0且a≠b,其參數(shù)p是連續(xù)且嚴格單調遞增的.從等式(1)~(3)和不等式(4)可得: H(a,b;0)=H(a,b) (5) G(a,b;0)=G(a,b) (6) 對所有a,b>0且a≠b成立. 受不等式(5)和(6)的啟發(fā),本文發(fā)現(xiàn)和證明了雙向不等式 H(a,b;λ1) G(a,b;λ2) 為證明本文的主要結果,需要以下相關基礎知識與引理. 分別是第一類和第二類完全橢圓積分且滿足下列等式[9]474-475: κ(0+)=ε(0+)=π/2,κ(1-)=+∞,ε(1-)=1, 引理1設-∞ 也在(a,b)上單調增加(減少).如果f′(x)/g′(x)的單調性是嚴格的,則F(x)和G(x)的單調性也都會是嚴格的[9]10. 引理2(1) 函數(shù)r[ε(r)-(1-r2)κ(r)]/r2在(0,1)上單調增加且值域為(π/4,1)[9]53; (2) 函數(shù)r[κ(r)-ε(r)]/r2在(0,1)上單調增加且值域為(π/4,+∞)[9]70; (3) 函數(shù)rε2(r)-(1-r2)κ2(r)在(0,1)上單調增加且值域為(0,1)[9]71; (4) 函數(shù)r[(2-r2)κ(r)-2ε(r)]/r4在(0,1)上單調增加且值域為(π/16,+∞)[9]71. 引理3函數(shù) 在區(qū)間(0,1)內是嚴格單調遞增的且值域為(3/2,2). 證明:設f1(r)=(1+r2)κ2(r)-π2/4,f2(r)=r2κ2(r).簡單計算可得: (7) f1(0+)=f2(0)=0, (8) (9) 從等式(9)和引理2(1)可知f1′(r)/f2′(r)在(0,1)內是單調遞增的.注意到: (10) 所以,引理3容易從引理1和等式(7)(8)(10)協(xié)同函數(shù)f1′(r)/f2′(r)的單調性得到. 引理4函數(shù) 在區(qū)間(0,1)內是嚴格單調遞增的且值域為(3,4). 證明:設g1(r)=(1+r2)2κ4(r)-π4/16,g2(r)=r2κ4(r).簡單計算可得: (11) g1(0+)=g2(0)=0, (12) (13) 其中, 簡單計算可得: (14) (15) 其中, g4(r)=(r4+2r2-3)κ2(r)-2(r4-r2-4)ε(r)κ(r)-5(r2+1)ε2(r)= (16) 由引理2的(1)~(4)和等式(16)可得: g4(r)>0 (17) 對所有r∈(0,1)成立. 從等式(13)~(17)可以得g1′(r)/g2′(r)在(0,1)內單調遞增.注意到: (18) 所以,引理4容易從引理1和等式(11)(12)(18)協(xié)同函數(shù)g1′(r)/g2′(r)的單調性得到. 定理1設λ1,μ1∈[0,1/2],則雙向不等式 H(a,b;λ1) 證明:根據(jù)H(a,b),B(a,b)和A(a,b)是關于a和b對稱且一階齊次的.不失一般性,假設a>b>0.設a=1,b=[(1-r)/(1+r)]2,r∈(0,1)和p∈[0,1/2].由等式(1)~(3)得: (19) (20) 由等式(19)和(20)容易得: (21) 其中,函數(shù)f(r)定義在引理3. 所以,由等式(21)和引理3協(xié)同函數(shù)r(1+r2)在(0,1)內單調遞增且值域為(1,2),不難得到(1+r2)f(r)在(0,1)內單調遞增.注意到: (22) (23) 所以,定理1容易從等式(21)(22)和(23)得到. 定理2設λ2,μ2∈[0,1/2],則雙向不等式 G(a,b;λ2) 證明:根據(jù)G(a,b),B(a,b)和A(a,b)是關于a和b對稱且一階齊次的,不失一般性,假設a>b>0.設b=[(1-r)/(1+r)]2,r∈(0,1)和q∈[0,1/2].由等式(1)~(3)得: (24) 由等式(19)和(24)容易得: (25) 其中,函數(shù)g(r)定義在引理4. 所以,定理2容易從等式(25)和引理4得到. 作為定理1和定理2的應用,可以得到推論1. 推論1雙向不等式 對所有r∈(0,1)成立. 綜上,近年來,完全橢圓積分與二元平均值的比較得到廣泛研究.本文建立了一個特殊擬算術平均關于單參數(shù)調和平均和單參數(shù)幾何平均的最優(yōu)不等式,得到了一個第一類完全橢圓積分的確界,所得結果改進了已有的相關不等式.該研究方法對從事二元平均值研究的愛好者具有一定的借鑒作用.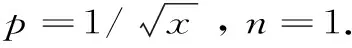

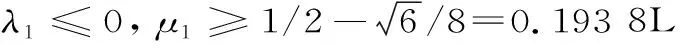
二、引 理
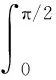

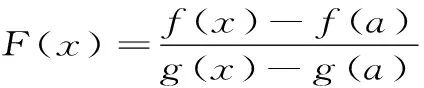
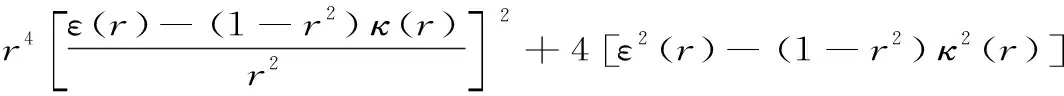
三、主要結果