切蛋糕切出來的三角形中位線*

劉 健

（黑龍江省大慶市教師發展學院 黑龍江大慶 163000）

三角形的中位線是平面幾何中一條非常重要的線段。如何引入三角形的中位線，讓學生感受三角形中位線的再創造過程一直是教學難點。教材中有多種引課，北師版教材采用的是在折紙中發現三角形的中位線，有的教材則直接給出問題讓學生完成證明，這兩種引課一個實際操作太難，另一個不能體現知識的再現。為了突破這個難點，能夠自然引入三角形的中位線，筆者經過多次嘗試最終在切蛋糕過程中產生了靈感，找到了一種能讓學生主動發現三角形中位線的方法。本文將呈現“三角形的中位線”的教學設計，供大家研討（參考北師大版教材）。

一、教材分析

根據《課程標準》（2022版），本節課要求學生探索并證明三角形的中位線。三角形中位線是繼三角形的“三線”（角平分線、中線、高線）后的第四種重要線段，但又不同于“三線”。教材從知識的整體性和聯系性考慮，將本節課放在平行四邊形之后。教材的設計力圖通過探索三角形中位線的過程，讓學生感受三角形和四邊形之間的相互轉化和知識間的內在邏輯關系，體會知識間的相互勾連，同時為學生面對一個新的數學問題提供研究思路。三角形中位線定理為判定兩直線的位置關系和論證線段倍分關系提供了新的方法和依據，也為后續學習相似三角形奠定了基礎。如何發現三角形的中位線，按照教材的設計在實際教學中操作難度太大，因此引課做了一些改動，重新設計了一個問題情境，從特殊的等邊三角形出發，然后拓展到一般，在這個過程中向學生隱性滲透從特殊到一般的研究思路，使得學生在獲得顯性知識的同時也有隱性的收獲。三角形中位線定理的得出是平行四邊形判定定理與性質定理的直接應用，前面運用連接對角線，把平行四邊形劃歸為兩個全等的三角形研究平行四邊形的性質，反之通過添加輔助線將三角形轉化為平行四邊形，然后利用平行四邊形的性質研究三角形的有關問題，在這個學習過程中讓學生充分感受化歸與轉化的數學思想，從而進一步提高學生分析問題、解決問題的能力。

二、教學目標

1.在切蛋糕的過程中，發現一條不同于三角形中線的線段——三角形的中位線，引發思考，進而開展研究。

2.能想到將三角形問題轉化為平行四邊形解決問題，體會轉化的數學思想，理解教材的設計意圖。

教學重點：證明三角形中位線定理。

教學難點：1.如何引導學生在切蛋糕的過程中發現三角形的中位線？

2.如何驗證三角形中位線定理？

三、教學過程設計

1.情境導入

7月9日是二年級小學生尚希的生日（圖1-1），尚希邀請了班級里的3個小朋友來到家里（圖1-2），尚希的爸爸端上來生日蛋糕如（圖2-1），蛋糕的水平截面是等邊三角形，生日蛋糕怎么平分啊（考慮到蛋糕表層有奶油和巧克力，所以只能豎直切刀）？

圖1-1 尚希的生日

圖1-2 分享

圖2-1 怎么分

2.質疑探究

活動1：發現三角形的中位線。

問題1：如何切蛋糕讓4個小朋友都滿意呢？如何將這塊蛋糕平均分成4份呢（圖2-1）？.

思考：如圖2-2，圖2-3所示，這兩種分法哪一種能讓小朋友都滿意呢？

圖2-2 分法一

圖2-3 分法二

問題2：尚希先切了一塊蛋糕給爸爸、媽媽，蛋糕的水平截面不再是等邊三角形了？還能平均分成4份嗎？

處理方式：問題1、2都是先讓學生自己切，然后再組內交流，重點交流你是怎么切的，是怎么想到這樣切的。

設計意圖：預設學生首先會想到利用中線的性質平均分得4塊，但是這種分法對于二年級的小朋友無法解釋4塊蛋糕大小相同，所以考慮其他的分法，既要平均分成4份，又要形狀相同，目的是引出三角形的中位線相關知識。

問題3：如圖3-1，圖3-2所示，是小朋友都滿意的切法，請你選擇其中一條線段描述這條線段的特征？

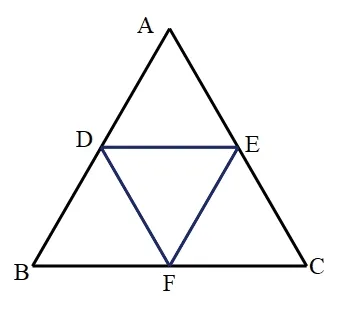
圖3-1

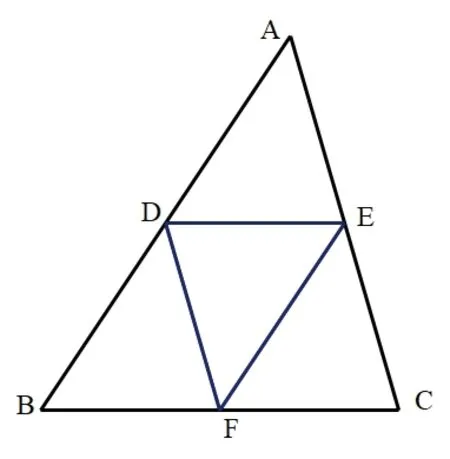
圖3-2

三角形中位線定義：____________________________。

問題4：①在三角形中，有幾條這樣的線段？②請你說出三角形中位線和中線的區別。

設計意圖：問題3完成具體到抽象的過程，得出三角形中位線的定義。問題4進一步明晰三角形中位線的特征。

活動2.猜想并證明三角形中位線定理。

猜想：問題5：已知線段DE為△ABC的中位線，觀察圖4，類比我們以往的學習經驗，你認為我們應該如何研究這條線段？

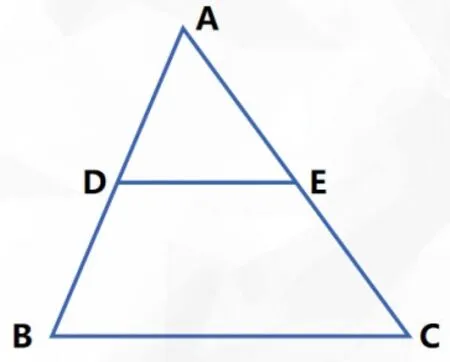
圖4

問題6：觀察圖4，你認為DE和△ABC的哪一條邊有關系？有什么關系？說一說你的猜想。

處理方式：讓學生通過觀察猜想DE與BC的關系，進行大膽猜想。

設計意圖：問題5讓學生體會研究問題的思路，研究三角形中位線的性質就是研究中位線與三角形組成元素之間的關系（位置關系與數量關系）；問題6是讓學生是自己發現DE與第三邊的關系，培養學生發現問題、提出問題的能力。

3.驗證猜想

（1）測量

（2）信息技術檢驗

處理方式：用GeoGebra（圖形計算器）軟件在白板上讓學生操作驗證猜想的正確性。

設計意圖：利用信息技術，讓學生直觀地感受猜想的正確性，獲得成就感。

（3）演繹推理證明

問題7：如圖5所示，你能用幾何推理證明上述結論嗎？觀察切完的蛋糕，你有什么想法？先獨立思考再小組交流。重點交流你怎么想的，怎么想到的？

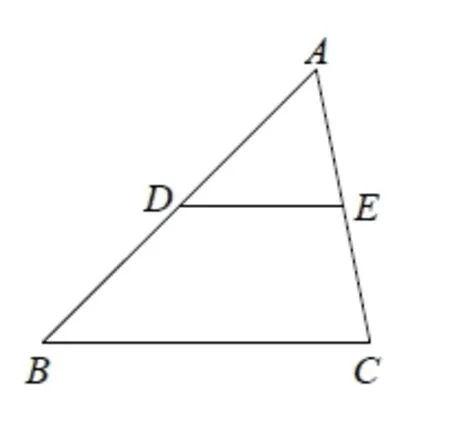
圖5

設計意圖：添加輔助線將三角形轉換成平行四邊形學是教學難點，為了突破難點。首先讓學生觀察操作后得到的圖形，然后進行獨立思考、小組交流，目的是在交流中有思維的碰撞，找到轉化的方法，揭示問題本質。

預設學生有可能添加的輔助線：如圖6-1，6-2，6-3所示。

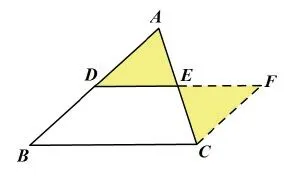
圖6-1

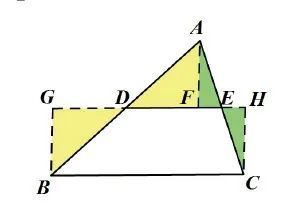
圖6-2

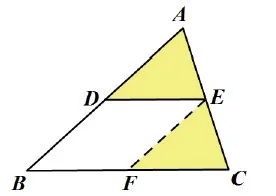
圖6-3

結論：

三角形中位線定理______________________________ 。

定理兩方面的含義：位置關系——平行，數量關系——倍分。

符號語言：______________________。

問題8.請你總結一下，我們是如何證明三角形中位線的。設計意圖：內化轉化的思想方法。

4.解決問題

（1）解決引課問題：教學處理：如圖7所示，回到引入中的“分蛋糕問題”。

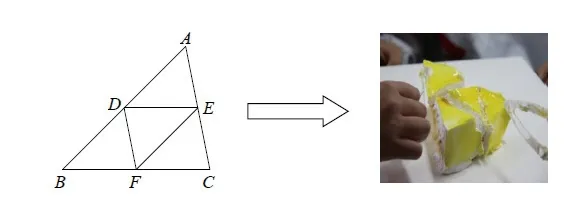
圖7 體會三塊蛋糕一樣大

設計意圖：肯定實踐操作的正確性，達到教學問題設計的前后呼應。

（2）例題

ΔA1B1C1如圖8中的（1）所示，在△ABC中，A1，B1，C1分別是邊BC，AC，AB的中點，（1）如果AB=12，BC=10，AC=8，求的周長。圖（2）A2，B2，C2分別是B1C1，A1C1，A1B1的 中 點，A3，B3，C3分 別 是B2C2，A2C2，A2B2的 中點，依此類推圖（3）.若△ABC的周長為a，面積為S，則ΔAnBnCn的周長為________，面積為________。

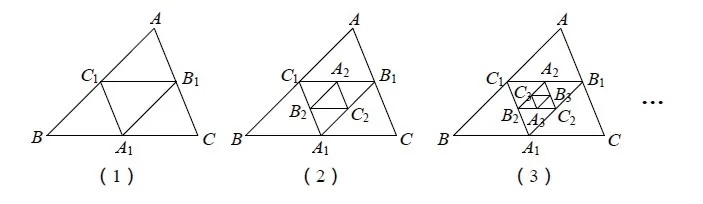
圖8

處理方式：（1）學生在黑板板書；（2）口答。

設計意圖：三角形中位線定理的直接應用。

（3）鞏固練習

如圖9所示，任意一個四邊形，以四邊形的中點為頂點組成一個新四邊形，試猜想這個新四邊形的形狀？并證明你的猜想。

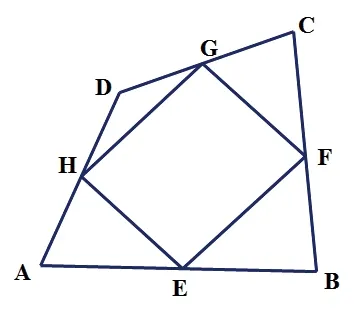
圖9

5.課堂小結

①敘述三角形中位線定理的內容。②你們是如何發現三角形的中位線的？說一說發現過程？你有什么感悟。③我們是如何證明這個定理的？在方法上，你有什么收獲？④你還有什么收獲？

結語

為了呈現一個自然、本質、樸實的課堂，筆者設計了一個貼近學生生活的問題情境，即分蛋糕的問題。在問題情境設計中的一個小細節就是選擇，小學低年級的小朋友，雖然利用三角形中線的性質可以平分蛋糕，但是形狀不同，怎么分才能不引起小朋友之間的矛盾呢？學生通過動腦、動手，相互合作交流、探究等多種學習途徑，發現三角形還有一條特殊的線段——三角形中位線，體現“再創造”的過程，進而產生研究這條線段的想法。整個教學過程自然、生動，達到了讓體會學生知識“再創造”的效果，培養了學生的創新能力。