在合作中優化 在交流中提升
王仕娜
河北省唐山市第十二高級中學
在高中數學教學中若能發揮好集體的智慧,通過互動交流,往往可以實現教學相長.筆者結合具體案例展示了生生合作和師生合作的價值,以期合作交流能更好地走進高中數學課堂.
1 生生合作,發掘學生潛力
在數學學習中,由于個體認知水平、思維方式等方面存在著差異,因此在解題時往往會出現多種解法,這也就為學生合作交流創設了良好的契機.在解題教學中若能充分發揮學生的主體作用,順應學生的思維,讓學生大膽嘗試,積極合作,在合作中體驗團隊合作的樂趣,則能很好地培養學生團隊意識,激發學習興趣.
案例1在△ABC中,角A,B,C對應的邊分別為a,b,c,若sinA=3sinCcosB,且c=2,則△ABC面積的最大值為.
師:請大家思考一下,這個問題該如何求解呢?(教師預留時間先讓學生獨立思考.)
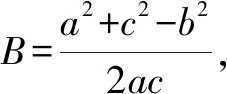
師:沒關系,能利用正弦定理和余弦定理得出a2+12=3b2,很不錯!結合三角形面積公式,看看是否能找到解題的突破口?
生3:我的運算過程稍微簡單一些.(學生正在為復雜的運算犯難時,聽說有更為簡單的方法,迅速被吸引.)
師:請說說你的想法.

生4:生3的運算過程還可以更簡單.(大家紛紛投來疑惑的目光.)
生4:當得到a=6cosB時,生3是將cosB用a表示出來,其實這步轉化是沒有必要的,可以直接將a=6cosB代入三角形面積公式,得
S△ABC=asinB=6sinBcosB=3sin 2B.
由于sin 2B≤1,因此S△ABC≤3.當sin 2B=1,即B=45°時等號成立,所以△ABC面積最大值為3.
師:非常好!經過一步步探究,同學們發現了解題的最佳方案.請大家參照幾位同學的解題過程,看看這幾種解法有哪些異同?各解法的本質又是什么?
本研究采用探索性因子分析方法來驗證結構效度。首先需要對數據進行KMO樣本測量和Bartlett球體檢測來判斷問卷是否適合做因子分析。一般KMO值在0.8以上,Bartlett球形檢驗的顯著水平(Sig.)<0.05表明可以做因子分析,本研究問卷的KMO 測量值>0.8,同時Bartlett球體檢測的顯著性概率<0.05,因此適合做因子分析。KMO和Bartlett的檢驗結果見表3。
生5:我們小組一致認為,從方法的本質上來分析,生2和生3運用的是“角化邊”,而生4運用的是“邊化角”.另外,生4在解題時還巧妙地運用了整體代入,使運算過程更加簡潔,大大節省了運算時間.
通過合作交流,不斷嘗試,實現了解題方法的不斷優化,進而達到事半功倍的效果.
2 師生互動,實現合作共贏
在教學過程中,讓學生積極參與進來,師生互動、合作交流,為學生營造一個開放的、輕松的學習環境,往往可以使師生共同成長.

本題是一道推理題,將平面幾何推廣至空間幾何,通過類比推理實現知識的拓展,體會“學以致用”的真正價值.
師:這個題目該怎么做呢?
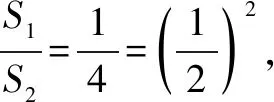
師:你們認為這個結論正確嗎?
師:你是怎么做到的呢?
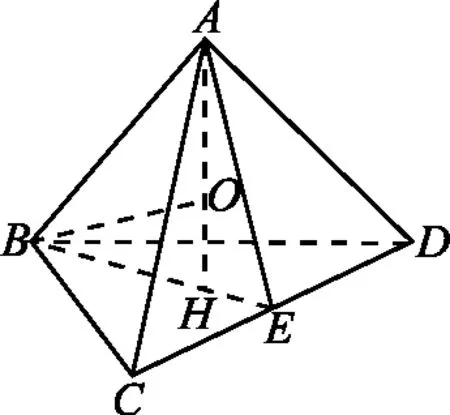
圖1
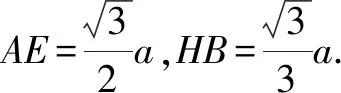
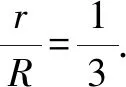
師:非常好,思路清晰,推理合理,值得大家學習.不過,本題是一道填空題,若運算過程復雜可能會影響解題的進度,這道題是否還有其他的解法呢?(大多學生也意識到了這個問題,已經有學生開始嘗試用其他方法演算了.)
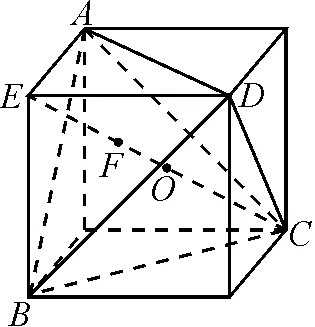
圖2
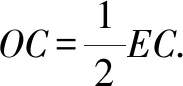
師:很好!解題時應用已有經驗簡化了運算過程,加快了求解的速度.
生4:我還有更簡單的方法.
師:哦!說說你的解題思路.
生4:我是受生3解題思路的啟發,生3是通過補圖法求解,而我嘗試用分割法求解.
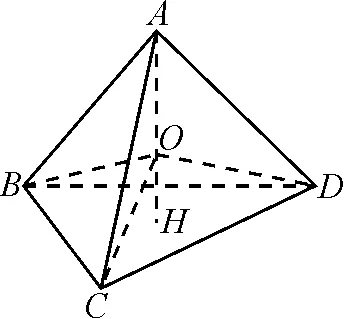
圖3
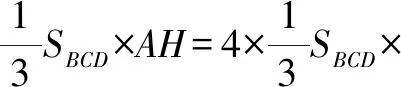
師:非常好!從補圖聯想到了分割,將割補法應用得淋漓盡致,經過轉化不僅使過程更加清晰易懂,而且大大降低了運算量,提升了解題速度.這個解題思路我也沒有想到,聽到生4的講解也深受啟發.
在教學過程中,生4分割法的給出也讓教師眼前一亮,驚嘆于學生無限的創造力.這也驗證了教學過程是動態變化的,即使精心預設也可能會發生一些“意外”.然這些“意外”往往就是新思路的生長點,在教學中教師要給“意外”提供生長的空間.當然,教學中也要有足夠的耐心解讀這些“意外”,這樣才能在“意外”中收獲更多的教學經驗,實現教學相長.
總之,在教學過程中,教師要給予學生足夠的時間進行合作交流,這樣不僅可以實現解題思路的優化,而且可以更加清晰地看到學生的優勢與不足,這對教學計劃的制定和教學目標的實施都有著積極的作用.同時,在此過程中教師的教學能力和知識儲備也會大大提升,實現了教學相長,合作共贏.Z

