淺談如何借助“意外”打造高質數學課堂
張 潔
湖北省大冶市第一中學
在新課改的推動下,數學課堂逐漸向多元化發展,更加關注學生主體作用的發揮,“自主、合作、探究”已成為高效數學課堂不可或缺的三要素,其在數學教學中發揮著不可估量的作用.為了提升數學課堂有效性,使課堂更加高效,教師在數學課堂上需要打破單一的、保守的“講授式”教學模式,將數學課堂打造成開放的動態課堂[1].為了打造高效動態的數學課堂,在教學中就需要引導學生經歷自主學習和合作探究,雖然在此過程中可能會出現一些不確定的因素,但這些“不確定”往往可能就是隱藏的意外驚喜.為此,在教學中,教師要鼓勵學生進行交流和探究,使不同思維碰撞出耀眼的火花,彰顯數學之美.
為了激發學生的積極性和探究欲,將課堂引入更深處,筆者結合教學中出現的“意外”,淺談了探究在數學教學中的重要意義,以期共鑒.
1 教學實錄
為了加深學生對圓錐曲線與方程的理解,教師在復習階段結合對下面一道例題的引導,以讓學生通過類比進一步實現知識的內化.
例已知兩定點F1(-2,0),F2(2,0),試分別求滿足下列條件的動點P的軌跡E的方程.
(1)|PF1|=|PF2|;
(2)|PF1|+|PF2|=6;
(3)|PF1|-|PF2|=2;
按照課前預設,該過程由小組探究合作完成,探究后學生板演求解過程,借助不同解題思路交流解題經驗,進而拓寬思維廣度.按照預期學生順利地完成了預設目標,教師想繼續進行下面的復習內容時,聽見有幾個學生在竊竊私語,他們在討論滿足|PF1|·|PF2|為固定值的動點P的軌跡方程該是什么樣子.面對教學中產生的這個“意外”,若教師選擇與學生一起探究可能會影響課程計劃,不利于教學目標的實現,但若置之不理將抹殺學生探究的積極性,不利于學習能力的提升,為此,教師選擇充分利用這次“意外”,讓學生通過探究消除疑惑,深化理解[2].
師:我們完成了前面四個題目,有些同學似乎又有新想法,我們一起來聽一聽.(教師引導學生大膽說出自己的疑惑.)
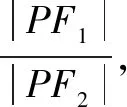
師:很好!確實我們上面只關注了|PF1|與|PF2|的“和、差、商”,忽視了“積”,那么這樣的曲線到底是什么呢?
師:現在大家思考一下|PF1|·|PF2|這個定值該如何表示?其與動點P到定點F1和F2的距離大小又有什么關系?(為了給學生指引探究的方向,教師將探究分成若干小問題,以淡化問題的抽象感,激發學生探究的熱情.)
生2:結合問題(2)和問題(3),設定值為a2,并且將a分成a>2,a=2,a<2三種情況進行比較.
師:很好!那么我們就從特殊值入手,看看從這三種特殊情況中能否發現一般規律.取a=1,2,3這三個特殊值來探究曲線的圖形.即|PF1|·|PF2|=12,|PF1|·|PF2|=22,|PF1|·|PF2|=32三種情況.那么我們該如何進行探究呢?
生3:應根據特殊值a=1,a=2,a=3分別求出曲線方程,接下來結合曲線方程的幾何性質逐一進行探究.
師:我們常用哪些幾何性質來探究呢?
生3:對稱性、頂點坐標、x的取值范圍等.
師:很好!看來大家已經掌握了研究解析幾何的精髓,實現“數”與“形”的相互轉化.現在一共三種情況,分三個大組進行探究,探究后請各小組參照表1的要求填寫求解結果.(教師根據學生反饋設計了表1,以讓學生更好地將各種情況進行類比,進而使計算結果更加清晰明了,便于學生觀察和理解.)
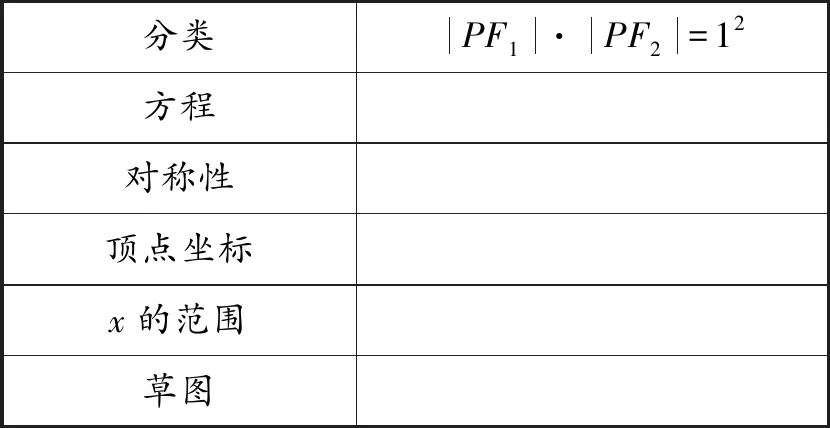
表1 曲線的圖形與性質
通過小組合作探究,各小組都順利地求解并繪制出了草圖.在關于對稱性的探究中,有些學生出現了思維障礙,教師借助師生交流的方式為學生釋疑.
師:對于對稱性你們是怎么驗證的呢?
生4:設點P(x,y)在曲線上,若點P關于x軸對稱,則對稱點P′(x,-y)也應在曲線上,代入后即可驗證曲線是否關于x軸對稱.同理,通過該方法還可以進一步驗證曲線是否關于y軸和原點對稱.
師:很好!我們根據x的取值范圍并結合曲線的對稱性繪制出了草圖,若我們想進一步精確繪制曲線圖形還需要知道什么?
生5:需要知道y的范圍.
師:那么y的范圍如何求解呢?
生6:可以利用求函數值域的思路求解.(生6的思路給出后,學生提出了質疑.)
生7:函數中x值與y值是一一對應的,曲線方程不能滿足這一條件,因此其轉化不等價,不能這樣求解.
師:那該如何實現等價轉化呢?
生8:剛剛已經知曉該曲線方程關于x軸,y軸和原點對稱,那么我們在求解時可以僅考慮第一象限的圖形,第一象限的圖形繪制完成后利用對稱性完成整個圖形的繪制.第一象限的x值與y值顯然是一一對應的,這樣就可以應用值域的思路求解了.
師:說的太好了!利用曲線方程的對稱性完成了函數與曲線方程的轉化,這樣,我們后期就可以利用研究函數的思路進一步研究曲線.
為了實現特殊向一般的轉化,教師引導學生借助曲線方程的一般形式繼續探究,其一般形式為[(x+c)2+y2][(x-c)2+y2]=a4(a>0).
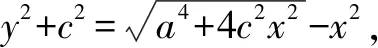
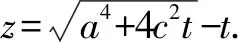
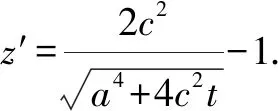
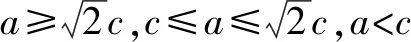
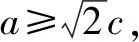
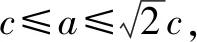
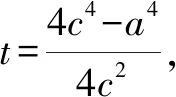
探究至此,學生可以結合圖形性質繪制出圖形.本節課雖然并未按照預期的效果完成預定教學目標,但通過利用“意外”學生收獲多多.通過類比探究不僅深化了對知識的理解,在此過程中函數與方程、特殊與一般的轉化也應用得淋漓盡致,大大地提升了課堂有效性.
2 教學反思
2.1 讓預設與生成同步發展
在教學設計階段,教師要善于從學生的角度進行思考,預判學生可能提出的問題,從而提前做出教學預案,這樣即使課堂中出現一些突發“小意外”時,教師也可以掌控教學方向,統籌全局.當然,只有教師課前精心地做好預設,課上才能及時捕捉這些“小意外”,實現精彩演繹.可見,預設與生成既對立又統一,教學中必須應用好這一對對立統一體,促進多元、動態課堂生成.
2.2 讓尊重扎根課堂
教學中要利用好思維差異的優勢,多鼓勵學生從不同角度提出問題,尊重學生的新想法和新思路,引導學生積極探究,進而達到發散思維、培養創新意識的目的.同時,教師要為學生營造平等、民主的學習氛圍,切勿只關注學優生的新思路而對學困生的問題置之不理,久而久之,勢必會挫傷學困生的積極性和自信心,不利于實現全員發展.
2.3 讓探究貫穿課堂始終
在新課改的推動下,學生的學習模式逐漸實現了由“接受式”向“探究式”的轉化,學生的學習模式也由“被動接受”向“主動建構”逐漸過渡,有助于課堂有效性的提升.同時,經歷探究使學生敢于聯想、勇于質疑、勤于思考,進而使學生的學習態度更加嚴謹,思維更加靈活,有助于學生自主學習習慣的形成.另外,通過探究,讓學生親身經歷知識生成的過程,有助于學生實踐能力和創新能力的提升.為此,在教學中,教師要鼓勵學生參與探究,去發現、去解決、去反思、去創新,進而使課堂變得生動又高效.
總之,課堂生成性資源是寶貴的教學資源,教師在教學中切勿只追求進度而忽視課堂生成性資源的利用,要鼓勵學生進行多角度、全方位地思考,引導其提出有價值的問題,讓學生在交流、合作、探究中不斷成長,進而培養學生良好的數學品質和數學素養,促進學生綜合能力全面提升.

