不同頻率的組合振蕩場下產生正負電子對*

羅蕙一 江淼2)? 徐妙華? 李英駿2)??

1) (中國礦業大學(北京)理學院,北京 100083)

2) (中國礦業大學(北京),深部巖土力學與地下工程國家重點實驗室,北京 100083)

吸收組合低頻外場提供的多個不同能量的光子發生躍遷可以在真空中激發正負電子對.本文探究了在組合振蕩場作用下,不同的外場頻率對正負電子對產生的影響,研究結果表明：與單個振蕩場類似,當雙振蕩場的頻率和約為 2.3mec2 時,電子對產量達到極值.在雙振蕩場的頻率和固定為 2.3mec2 的情況下,對不同組合頻率下正負電子對的產量以及能譜分布進行了研究,發現當兩場頻率差較小時,電子對產量隨時間演化會出現顯著的“拍”現象.還發現兩個振蕩場頻率差越小,電子對的單能性越好;場頻率差越大時,電子對的產量越高、能譜范圍越寬.通過對躍遷概率分布圖的比較和分析,發現主要原因是頻率差較大時能夠發生顯著躍遷的多光子躍遷形式數量增加,從而促進正負電子對(尤其是高能端電子對)的產生.

1 引言

量子電動力學可以用于精確描述帶電粒子與電磁場相互作用,在強電磁場作用下真空衰變產生正負電子對是量子電動力學的重要預言之一.1951 年Schwinger[1]給出了可以使真空發生衰變產生電子對的電磁場的最低強度,對于一個空間均勻且不隨時間變化的電場,產生真空極化的閾值為Ec=1.32×1016V/cm,相應的激光強度需要達到1029W/cm2.這一強度目前還無法利用現有實驗條件實現,包括一些正在建造的超高功率激光器.然而強場狀態下的輻射發射和電子對產生幾乎已成為每個激光設施計劃下實驗項目的一部分.目前產生正負電子對的實驗一般通過重離子碰撞[2,3]、激光與高能電子束相互作用[4,5]、以及激光與原子核相互作用[6]來實現.僅由超強激光場直接引起正負粒子產生的實驗還無法開展.隨著激光技術的快速發展,實驗中的激光強度將進一步接近這一閾值,并有望在不久的未來達到擊穿真空的閾值條件,這對人類探索科學邊界的推動將是巨大的.

理論方面,目前研究真空中正負電子對的產生已有多種方法,例如世界線瞬時技術[7,8],DHW 形式[9?11],量子Vlasov 方程解法[12?14]、計算量子場論[15?17]等.國內外研究組針對各種外場情況下的粒子產生過程進行了詳細的研究[18?22].研究表明主要有兩種不同的機制可以從真空中產生正負電子對.一般通過Keldysh 參數γK=mecω0/(eE0)來劃分這兩種機制.當γK?1 時,正負電子對產生主要源于隧穿機制[23,24],這種機制要求穩恒電場的強度超過Ec=1.32×1016V/cm .當γK?1 時,可看作是微擾的過程,此時產生機制為多光子效應[25],即通過同時吸收幾個光子的能量使正負能態之間縱向耦合,這種機制需要外場隨時間快速振蕩.

在第二種機制中,當一個光子的能量大于能帶間隙 2mec2的時候,真空中的正負能態通過光子躍遷效應發生交疊,從而產生正負電子對.此前的研究已經表明在單個頻率大于 2mec2的振蕩場情況下,通過吸收單光子能量可以持續激發電子對[26].然而這要求外場超高速振蕩,因此在實驗上較難實現.此外,多個光子的能量之和如果能夠越過能帶間隙,同樣也可以激發出正負電子對.本文將采用兩個振蕩場組合的模型,此前的研究表明,這時產生粒子對的臨界條件主要由場的頻率w決定,即使是亞臨界的場仍然可以通過光子躍遷觸發粒子對產生[27].本文將重點研究雙振蕩場情況下外場頻率對多光子躍遷產生正負電子對的影響.

2 方法及模型

本文使用計算量子場論的方法來描述強場下真空中正負粒子的產生過程,這一方法可以實現在全空間和時間上數值求解狄拉克方程[28,29].

描述粒子和反粒子的與時間相關的場算子Ψ?(z,t)滿足與時間相關的狄拉克方程.這里將模型簡化至一維,將狄拉克方程寫成如下形式(原子單位制):

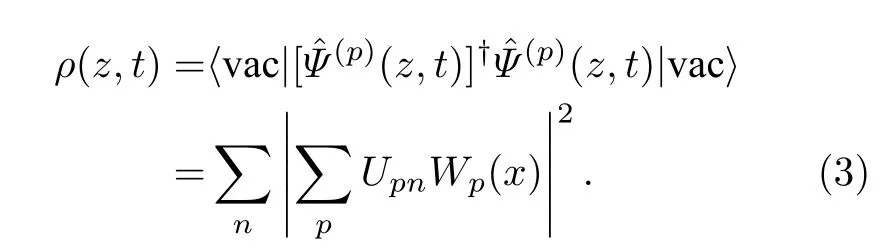
最后,將空間密度在全空間進行積分,可得出t時刻的粒子產生數:

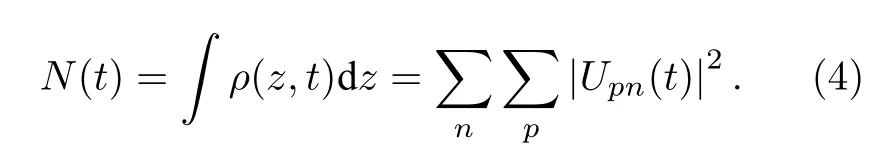
可以看到產生的粒子數目主要是由Upn(t) 來決定的.本文運用劈裂算符的方法[30,31]和快速傅里葉變換對狄拉克方程進行數值求解.運用劈裂算符的方法可將其中一步的演化算符定義為.通過推導簡化可以得到對應空間和動量的等效時間演化算符,將其與快速傅里葉變換的方法結合演算,就可以完成一個完整的演化步驟.

本文研究組合雙振蕩場下正負電子對的產生,所取的外場V(z,t) 為兩個頻率不同的隨時間振蕩的空間局域場的組合,表達式為V(z)=V1S(z)sin(ω1t)+V2S(z)sin(ω2t),其中w為場的振蕩頻率,V表示勢的高度,下文模擬中兩個振蕩場V1,V2均為 2.0c2.S(z) 為 Sauter 勢,其表達式為S(z)={1+tanh[(z ?z0)/W]}/2,其中W表示振蕩場的場寬,z0表示勢場的中心.通過前面介紹的方法可以對雙振蕩場情況下的狄拉克方程進行數值求解,得到不同頻率組合場下粒子對產量隨時間的演化過程.

3 外場頻率對多光子躍遷過程的影響

在多光子躍遷效應中,外場振蕩頻率w直接決定光子的能量,因此正負粒子的產生數與兩個振蕩場的頻率ω1和ω2緊密相關.圖1 顯示的結果是t=0.003時刻的電子對數量與振蕩場頻率的關系.將雙振蕩場中一個場的頻率ω1固定,另一個場頻率ω2在 0—4.0c2范圍內變化.這里設置外場寬度W=2/c,場強為V1=V2=2.0c2,圖中的虛線分別對應于將雙振蕩場中的ω1固定為1.5c2,1.6c2,1.7c2,1.8c2.作為對比,黑色實線給出了單個振蕩場情況下不同頻率的場激發的電子對數量.

從圖1 可以看出,對于單個振蕩場,正負電子對產量隨著頻率呈現先增長后降低的趨勢,在頻率為 2.3c2左右達到極值,這與文獻[27,32]中的結果是符合的.對于雙振蕩場來說,在一個場(ω1)為次臨界場的情況下,由于另一個次臨界場(ω2)的加入,電子對產量在 0<ω2<2.0c2區間內有顯著的提升.同時,對于兩個次臨界組合振蕩場來說,正負電子對產量隨組合場頻率之和的變化也呈現出先增長后降低的特征,與單個振蕩場的變化規律一致.以ω1=1.5c2的數據為例,從圖1 可以看出,當ω2為 0.7c2—0.8c2時,正負電子對的產量達到一個極值,此時兩個組合場頻率之和為 2.2c2—2.3c2,與單個振蕩場峰值頻率相符合.對于ω1為1.6c2,1.7c2,1.8c2的數據來說,均呈現出相同的規律.由于越靠近 2.0c2的位置能態密度越大,且能態分布有一定寬度,因此,在目前的模擬參數(主要是勢場高度V和場寬W)給定的情況下吸收 2.2c2—2.3c2的光子能量時相互作用的態比剛好等于 2.0c2時更多.這是導致正負電子對產量在單個振蕩場頻率和雙振蕩場頻率之和均在 2.2c2—2.3c2左右時達到峰值的原因.

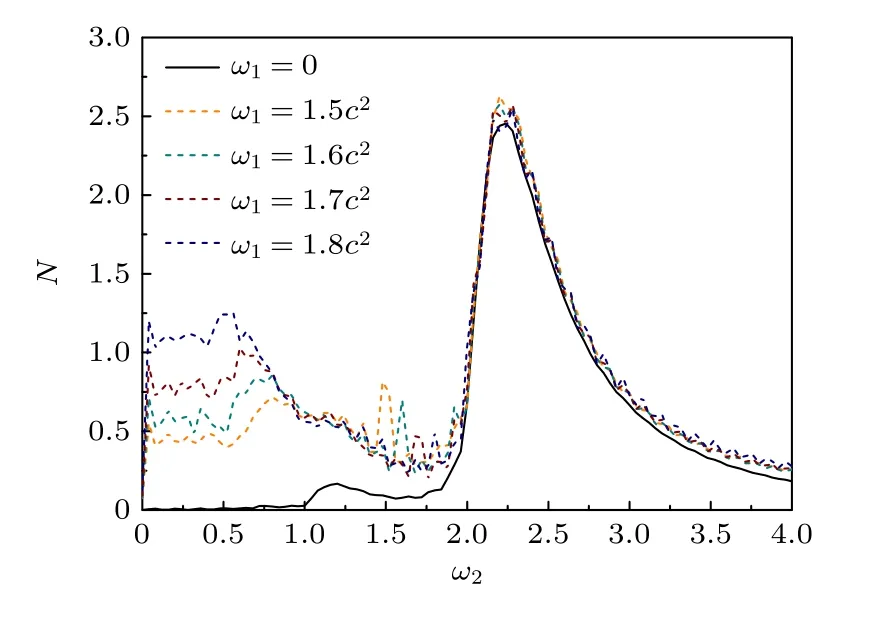
圖1 雙振蕩場情況下粒子對數量隨外場頻率 ω2 的變化關系圖(t=0.003 時刻),勢場高度 V1=V2=2.0c2,寬度W=2/c.黑色實線為單個振蕩場下的粒子對數量與頻率的關系Fig.1.The dashed lines give the total number of created pairs for different combined frequencies at t=0.003 ,V1=V2=2.0c2,and width is W=2/c .The black solid line illustrates the number of created pairs when only one oscillating field is presented.

從圖1 還可以看到,當兩個振蕩場的頻率相等時,電子對產量也會達到一個極值,同時不同頻率下電子對產量增加的程度不同.Jiang 等[26]在此前的工作中已經對這一現象進行了解釋.

3.1 場頻率和固定時的粒子對隨時間演化

在雙振蕩場的情況下,當組合場頻率之和約為2.3c2時電子對產量會出現峰值,所以在后續模擬中將雙振蕩場的頻率之和固定為 2.3c2.圖2(a)中不同顏色的實線給出了頻率和ω1+ω2=2.3c2不同組合頻率的粒子對產量的時間演化曲線,兩條虛線分別為ω=1.8c2,1.9c2的單振蕩場的結果.

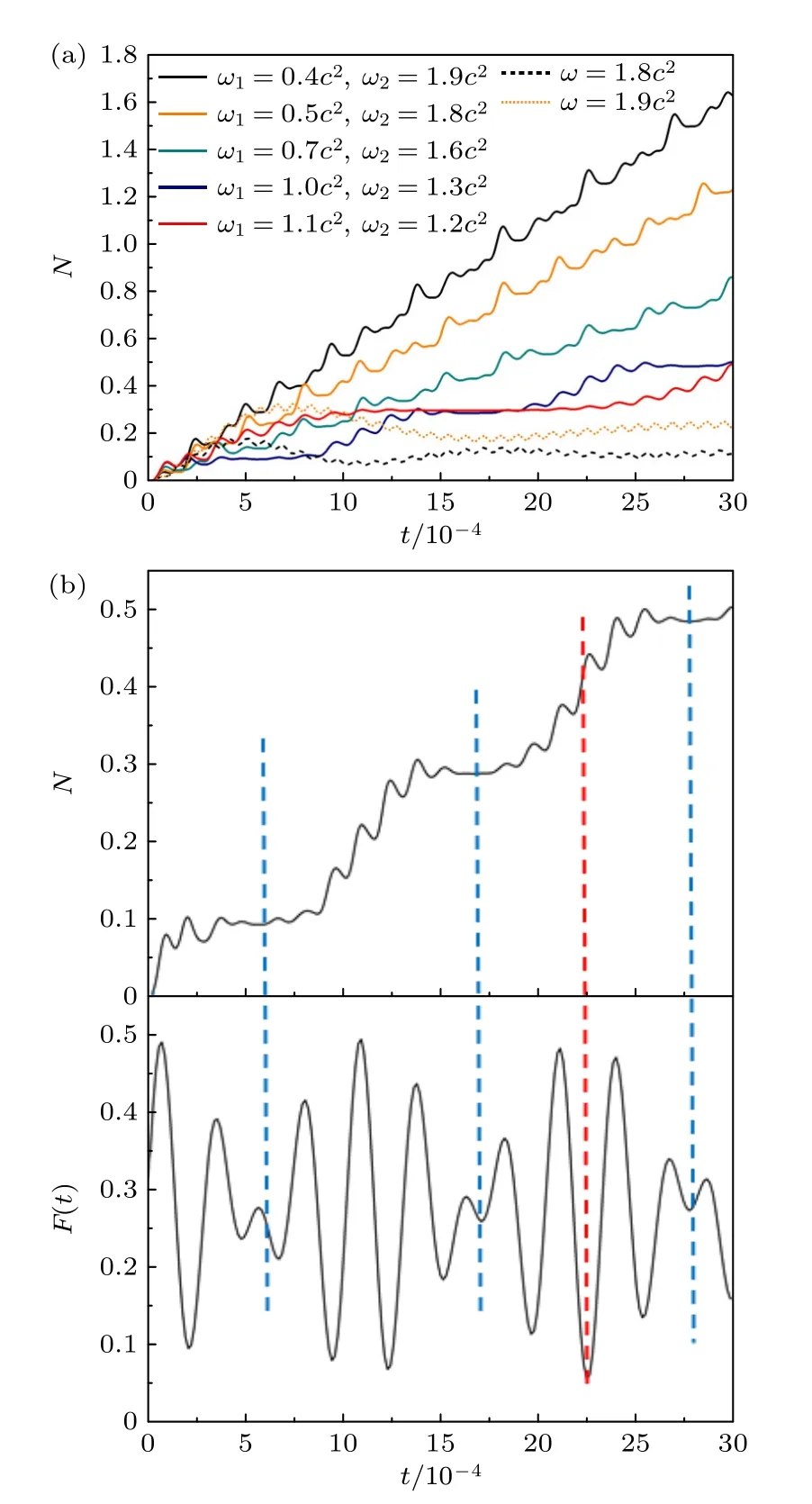
圖2 (a)保持雙振蕩場頻率和均為 2.3c2 時不同組合場頻率下電子對產量 N 隨時間的演化圖;(b) N(t) 與 F (t) 的對比圖,上半 部分為 ω1=1.0c2,ω2=1.3c2 時的 N(t) 曲 線,下半部分是相同條件下 F(t) 的示意圖.勢高V1=V2=2.0c2,場寬W=2/cFig.2.(a) Time evolution of the total number N of created electron-positron pairs under different combined frequencies.The sum of the frequencies of the two oscillating fields are kept as 2.3c2 .(b) Comparison of the time evolution of pair production N(t) and f (t) .The upper part is the N(t)figure for ω1=1.0c2,ω2=1.3c2 and the below part is the sketch of F(t) under the same conditions.V1=V2=2.0c2 ,W=2/c .

對比單個振蕩場和雙振蕩場的長時效應下的斜率可以發現,單個次臨界振蕩場作用下電子對產生率接近于0,而在兩個次臨界振蕩場的共同作用下電子對產生率有顯著的增加,可實現隨時間持續地產生.其次,從圖2(a)可以看到電子對產率隨時間出現周期性的變化.這個周期與兩個場的頻率差有關,頻率差越大,周期性變化越快.我們認為導致產率隨時間出現周期性變化的原因是雙振蕩場疊加后合成場振幅隨時間發生的振蕩.根據組合場模型,兩個場隨時間的振蕩由F1(t)=sin(ω1t) 和F2(t)=sin(ω2t)給出.由于兩個場在空間中處于完全相同的位置,所以總電場隨時間變化的形式為F(t)=2sin[(ω1+ω2/2)t]cos[(ω1?ω2/2)t].

圖2(b)上半部分對應于圖2(a)中藍色實線ω1=1.0c2,ω2=1.3c2時電子對產量隨時間的演化曲線,下半部分則是這一頻率參數下根據上述F(t)的表達式給出的合成電場隨時間振蕩的圖像.對于光子吸收引起的粒子對產生,粒子的產生率與激光場的強度以及光子吸收的個數相關,呈現A2n的規律,其中A為激光場的振幅,n為光子吸收個數.當ω1≈ω2時,合成場振幅在時間上出現明顯“拍”現象.在合成場的振幅A接近于 0 的時刻(如圖2(b)中藍色虛線所示),對應于N(t) 曲線上出現的平臺區,此時電子對產率 dN/dt接近于 0.在合成場的振幅A最大的時刻(如圖2(b)中紅色虛線所示),電子對的產量隨時間快速增長.由此出現了電子對產率隨時間出現周期性變化的現象.同時,平臺區的存在也導致電子對產量在ω1≈ω2的情況下受到抑制.此外,在N(t) 圖中還能觀察到短周期的小幅振動,這一振動周期主要取決于兩個振蕩場的頻率和.

此外還發現,長時效應下的電子對產率dN/dt與兩個振蕩場的頻率差緊密相關.當ω1=1.1c2,ω2=1.2c2時,電子對的平均產率約為 dN/dt=95.4,當ω1=0.8c2,ω2=1.5c2時,平均產率約為dN/dt=230.9,變為原來的 2.4 倍,當ω1=0.4c2,ω2=1.9c2時,電子對平均產率提升為 dN/dt=545.3,變為原來的 5.7 倍.可見,在雙振蕩場的頻率和固定為2.3c2的情況下,隨著兩個振蕩場的頻率差越大,電子對產率越高.后續將進一步討論這一現象的原因.

3.2 場頻率和固定時的粒子能量分布

同時,對兩個振蕩場頻率之和為 2.3c2時不同組合頻率下產生的正負電子對的能量分布進行了細致的模擬.將概率密度分布只對負能態求和,即可得出粒子在正能態上的分布.再通過動量和能量的轉換,可得出產生的電子對在能量上的概率分布.圖3 給出的是t=0.003 時刻的電子對能量分布概率圖.其中5 組數據對應的組合場頻率分別為ω1=0.4c2,ω2=1.9c2;ω1=0.5c2,ω2=1.8c2;ω1=0.8c2,ω2=1.52;ω1=1.0c2,ω2=1.32;ω1=1.1c2,ω2=1.2c2.

圖3 保持雙振蕩場頻率之和為 2.3c2 時五組不同組合頻率下產生粒子的能量分布概率.演化時間 t=0.003 a.u. .勢高 V1=V2=2.0c2,場寬W=2/cFig.3.The energy distribution of the particles created with two oscillating fields with different combined frequencies at t=0.003 a.u..V1=V2=2.0c2,W=2/c .

從圖3 可以看到組合雙振蕩場的兩場頻率差|ω1?ω2|越大,電子對產量越高.這一結果與圖2(a)中給出的電子對產率的結果是一致的.此外,從圖3可以看到兩場的頻率差越大,產生粒子的能譜整體上呈現更加分散的趨勢.當ω1=1.1c2,ω2=1.2c2和ω1=1.0c2,ω2=1.3c2時,產生的粒子能量基本上集中在 1.1c2—1.2c2附近,能譜峰的半高全寬約為 0.2c2,單能性相對較好.當ω1=0.8c2,ω2=1.5c2時電子對總產量增大,而且在高能端出現了更多的電子分布.當ω1=0.5c2,ω2=1.8c2時,電子產量進一步增大,且能譜上出現了兩個明顯的峰,能譜范圍顯著展寬.當ω1=0.4c2,ω2=1.9c2時,高能端粒子的占比已顯著大于低能端的粒子.

由于本文使用的是空間局域化的外場,并不是完全均勻的,粒子會發生動量不守恒的非對稱躍遷,所以僅通過正能部分的能量分布無法準確判斷粒子從負能態躍遷到正能態的躍遷形式和概率.為了進一步理解上述電子對產量和能譜分布的規律,接下來將結合躍遷能量概率分布圖來觀察不同組合頻率下電子對產生的躍遷情況.通過導出某一個能量為En的負能態與另一個能量為Ep的正能態之間的交疊概率,并比較各能態之間的交疊概率分布可以更深入地理解電子對產生的過程,同時對上述規律進行解釋.

圖4 給出的是三種組合頻率場下電子對躍遷能量概率分布圖.圖4(a)中ω1=0.5c2,ω2=1.8c2,圖4(b)中ω1=0.8c2,ω2=1.5c2,圖4(c)中ω1=1.0c2,ω2=1.3c2.圖中的水平軸和垂直軸分別表示負能量狀態和正能量狀態,水平軸與垂直軸相交的每一個點都對應于某一負能態到某一正能狀態之間的躍遷,這些點對應的顏色深淺表示該點吸收橫縱軸相加Ep+En的能量發生躍遷的概率大小.為方便觀察,圖中繪制的躍遷概率以對數形式 l og(p) 給出.

從圖4 的比較中可以看出: 當兩個場的頻率和固定為 2.3c2時,頻率差越大,能發生顯著躍遷的躍遷形式就越多.以圖4(a)為例,躍遷概率大于10?6的躍遷形式有 4 種,包括ω1+ω2,2ω1+ω2,3ω1+ω2,4ω1+ω2.當兩個場的頻率差越小,能發生顯著躍遷的躍遷數則越少.以圖4(b)為例,躍遷概率大于 10?6的躍遷形式僅有2個,僅包括ω1+ω2和2ω1+ω2.對于圖4(c)的情況,躍遷概率大于10?6的躍遷數目僅有 1 個,即ω1+ω2.在圖4 的3 個圖中,均包含顯著的吸收ω1+ω2形式的兩個光子發生躍遷的情況,這一躍遷產生的正負電子對的能量主要分布在1.1c2—1.2c2左右,這是在圖3 給出的5 組能譜分布中均出現 1.1c2—1.2c2的能譜峰的原因.當雙振蕩場的頻率差越大時(意味著低頻場頻率越低),則更多的多光子吸收的躍遷能量處于能態密度較大的位置.此時除了雙光子躍遷具有較大的概率以外,多種多光子躍遷過程對正負電子對產生的貢獻增強.其中三光子躍遷和四光子躍遷過程的概率甚至與雙光子躍遷的概率具有相同的數量級.從圖4(a)可以看到,對于ω1=0.5c2,ω2=1.8c2的情況即使在 4ω1+ω2的位置上仍能發生顯著躍遷,這對應于同時吸收4 個ω1和1 個ω2光子發生的多光子躍遷過程.此時產生的正負電子對的能量可以達到 1.9c2左右.這是雙振蕩場的頻率差較大的情況下電子對的產量增大、能譜擴展到高能端發生顯著展寬的主要原因.同時,由于所加振蕩場的空間局域化(W=2/c),非對稱躍遷也可以發生.從圖4(a)可以看到對于ω1+ω2,2ω1+ω2,3ω1+ω2,4ω1+ω24 種躍遷過程來說,非對稱躍遷均有較大的概率,因此能譜將在對稱躍遷的基礎上得到進一步展寬.

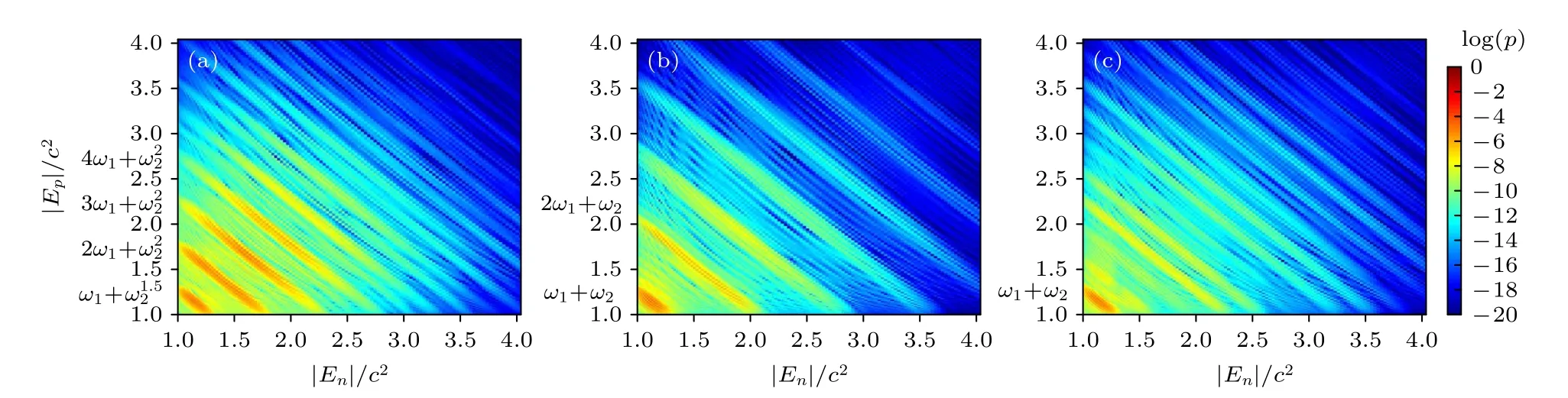
圖4 雙振蕩場下粒子躍遷能量概率分布圖 (a) ω1=0.5c2,ω2=1.8c2 ;(b) ω1=0.8c2,ω2=1.5c2 ;(c) ω1=1.0c2,ω2=1.3c2.勢高 V1=V2=2.0c2,場寬W=2/cFig.4.The probability distribution of transitions with different frequency combinations: (a) ω1=0.5c2,ω2=1.8c2 ;(b) ω1=0.8c2,ω2=1.5c2;(c) ω1=1.0c2,ω2=1.3c2 .V1=V2=2.0c2 .W=2/c .

考慮到外場寬度對多光子躍遷和正負粒子產生過程具有重要的影響[32],本文還對更寬的場寬下組合雙振蕩場中頻率對正負粒子產生的影響進一步進行了模擬.圖5 給出了場寬W=5/c時的躍遷能量概率分布圖和產生粒子的能量概率分布.

圖5 場寬為 W=5/c 時(a) ω1=0.4c2,ω2=1.9c2 和(b) ω1=1.0c2,ω2=1.3c2 的概率分布圖.(c)不同組合頻率下粒子的能量概率分布.勢高V1=V2=2.0c2Fig.5.The probability distribution of transitions with W=5/c: (a) ω1=0.4c2,ω2=1.9c2 ;(b) ω1=1.0c2,ω2=1.3c2 .(c) The energy distributions of the particles at t=0.003 a.u. .V1=V2=2.0c2 .

通過與圖4 的比較可以看出,在場寬較大時,高階多光子躍遷形式相對于前面窄場的情況發生了削弱,同時非對稱躍遷的概率也顯著減小,因此產生的粒子對數量小于窄場的情況,同時粒子的能量分布也更為集中.從不同的組合頻率對粒子對產生的影響上來看,在寬場情況下,頻率差較大(ω1=0.4c2,ω2=1.9c2)的雙振蕩場相對于頻率差較小(ω1=1.0c2,ω2=1.3c2)的情況仍然具有更多更強的高階多光子躍遷形式,因此總體產量更高,高能粒子更多.

綜上所述,結合電子對躍遷概率分布圖,對雙振蕩場情況下不同組合頻率對正負電子對產量與其能量概率分布的影響和規律進行了很好的解釋.

4 結論

本文基于計算量子場論,以劈裂算符和快速傅里葉變換為基礎的模擬方法對狄拉克方程進行全空間和時間上的數值求解,詳細討論分析了振蕩場作用下真空中產生正負電子對的過程,研究了兩個次臨界振蕩場情況下場的頻率參數對電子對產生的影響.研究結果表明,對于次臨界頻率場,通過兩個組合場的方式可以有效產生正負電子對.在場頻率之和約為 2.3c2時電子對產量達到極值.在兩場的頻率和固定為 2.3c2的情況下,對不同頻率組合下電子對的產量以及其能量概率分布的研究表明: 兩個振蕩場的頻率差越大,能發生顯著躍遷的多光子躍遷的形式越多,電子對的產量(特別是高能端電子對產量)越高,而且產生的粒子整體上能量分布的范圍越寬.