基于低損光學相變和超透鏡的可控多阱光鑷*

王焱 彭妙 程偉 彭政 成浩 臧圣寅 劉浩 任孝東 帥雨貝 黃承志 吳加貴 楊俊波

1) (西南大學人工智能學院,重慶 400715)

2) (國防科技大學物質與材料科學實驗中心,長沙 410073)

3) (西南大學物理科學與技術學院,重慶 400715)

4) (西南大學藥學院,發光與分子傳感教育部重點實驗室,重慶 400715)

5) (國防科技大學前沿交叉學科學院,長沙 410073)

為提升光鑷在三維空間中對粒子的捕獲性能,本文設計和分析了新型的雙阱和多阱超透鏡光鑷方案.首先基于低損耗相變材料Sb2S3設計了可控超透鏡雙阱光鑷,并對兩個半徑為250 mm 的SiO2 粒子所受光力進行了矢量橫向分析和軸向分析.仿真實驗結果表明,當Sb2S3 在晶態下時,超透鏡捕獲的兩個粒子的橫向光阱剛度 kx分別 達到了約25.7 pN/(μm·W)和37.4 pN/(μm·W),軸向光阱剛度 kz 均約為10.0 pN/(μm·W);而當Sb2S3 在非晶態下時,kx 和 kz 值均降低到其對應晶態下的1/10,且此時粒子在z 方向上不能被穩定捕獲,從而實現了在三維空間中對粒子的可控捕獲.進一步本文給出了陣列式的可控多阱光鑷.通過調控相變材料Sb2S3 的晶態和非晶態,能形成不同組合粒子的三維捕獲方案.這些新型可控光鑷可實現多種方式的三維空間粒子捕獲,提高了光鑷的靈活性,為超透鏡在光鑷領域中的應用提供了一種新思路.

1 引言

光鑷可以實現對多種粒子的非接觸式捕獲和操縱,在生物學領域和物理學領域發揮著重要的作用[1?9].近年來,多阱光鑷逐漸成為研究的熱點[10?13],其在細胞分類、微粒之間的作用力測量和光鑷成像打印等方面的應用,顯著提升了光鑷系統的捕獲性能[14].目前多阱光鑷可通過全息光鑷技術、多光束干涉、光纖成像等方法來實現[15?20],可實現對多粒子的同時捕獲和操縱.

隨著超表面技術的快速發展,超透鏡憑借著高集成性和超高數值孔徑(numerical aperture,NA)等優勢,逐步應用于光鑷領域,并對納米級粒子進行捕獲和操縱[21?26].然而,在多阱光鑷方面,相應的超透鏡研究較少,且僅僅處于初步階段.2017 年,Ma 等[27]實現了偏振敏感的多焦點渦旋超透鏡對微粒的捕獲和操縱.2021 年,Li 等[28]將光鑷和光扳手集成在一個超透鏡上,形成雙焦平面來對粒子進行捕獲和操縱.然而,目前多阱光鑷的超透鏡不能實現對多焦點的可控操作,只能完成一種方式的粒子捕獲,這嚴重限制了多阱光鑷對粒子捕獲的靈活性和高效性.

基于此,本文首先設計了基于低損相變材料Sb2S3和超透鏡的可控雙阱光鑷,用于對粒子的可控三維 (3D) 捕獲.在入射光功率保持一定的情況下,當Sb2S3處于晶態時,SiO2粒子可以被穩定的3D 捕獲;而當Sb2S3處于非晶態時,SiO2粒子在z方向上不能被穩定捕獲,從而實現對粒子可控3D 捕獲.在此基礎上,為進一步提升光鑷的捕獲性能,本文又設計了基于低損相變材料Sb2S3和超透鏡的多阱光鑷,同樣實現了粒子的可控3D 捕獲,并可靈活操縱粒子,形成不同形狀的圖案.

2 基于光學相變和超透鏡的可控雙阱光鑷

2.1 超透鏡設計

相變材料通過在晶態和非晶態之間的復折射率n=n+ik的顯著變化而實現對光場的調控.其中,Ge2Sb2Te5(GST)[29]和Ge2Sb2Se4Te1(GSST)[30]為目前常用的相變材料.但在近紅外波段,GST 的晶態損耗(k=1.49)和非晶態損耗(k=0.12)均較大,而GSST 在晶態的損耗也較大.與之相比,Sb2S3的晶態和非晶態的損耗k均可小于10–5,且其相變溫度(270 ℃)也較低[31],是極具應用前景的新型超低損耗光相變材料.圖1 展示了本文設計的基于低損相變材料Sb2S3的超透鏡結構,可用于實現可控雙阱光鑷.其中超透鏡的直徑為25 μm,工作波長為1064 nm,入射波長為右旋圓偏振光(right-handed circularly polarized light,RCP),輸出光場為左旋圓偏振光 (left-handed circularly polarized light,LCP).超透鏡由低損相變材料Sb2S3納米方柱、ITO 層和SiO2基底組成,并被分為A (y>0) 和B (y<0) 兩個部分,每個部分都可以實現Sb2S3納米方柱晶態和非晶態之間的互相轉換.當Sb2S3的納米方柱為紅色時,其狀態為晶態,光可以透過;當Sb2S3的納米方柱為藍色時,其狀態為非晶態,光基本不能透過.圖1(a)所示為A 和B 兩部分的Sb2S3均處于晶態時,可以形成兩個焦點.圖1(b)為A 部分的Sb2S3處于晶態,B 部分的Sb2S3為非晶態時,只在A 部分可以形成焦點.圖1(c)為A 部分的Sb2S3處于非晶態,B 部分的Sb2S3處于晶態時,只有B 部分可以形成焦點.圖1(d)為A 和B 兩部分的Sb2S3均處于非晶態時,兩部分均沒有形成焦點.因此,在入射光功率保持一定的情況下,只需要調控Sb2S3的狀態,便可以靈活調整超透鏡的聚焦狀態.

圖1 用于雙阱光鑷的超透鏡結構圖 (a) A 和B 部分的Sb2S3 均處于晶態;(b) A 部分的Sb2S3 處于晶態,而B 部分的Sb2S3 處于非晶態;(c) A 部分的Sb2S3 處于非晶態,B 部分的Sb2S3 處于晶態;(d) A 和B 部分的Sb2S3 均處于非晶態Fig.1.Structure of dual-trap optical tweezer metalens:(a) Sb2S3 in both parts A and B are in crystalline state;(b) Sb2S3 in part A is in crystalline state,while Sb2S3 in part B is in amorphous state;(c) Sb2S3 in part A is in amorphous state,and Sb2S3 in part B is in crystalline state;(d) Sb2S3 in both parts A and B are in amorphous state.

超透鏡的A (y>0) 和B (y<0) 部分分別對應兩種不同的相位分布,A 部分所對應的相位分布為

B 部分所對應的相位分布為

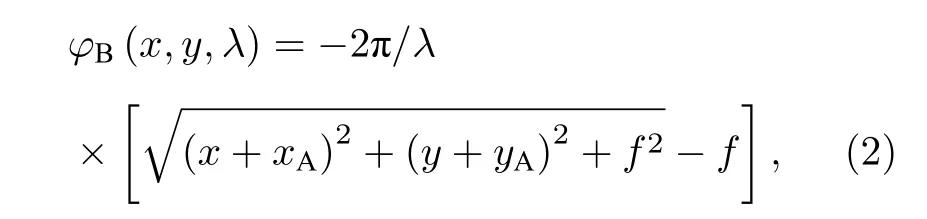
其中,(x,y) 代表超透鏡表面的坐標,(xA,yA) 為焦點坐標,λ為入射波波長,f為焦距.焦點坐標(xA,yA)=(5 μm,0),A 和B 部分焦距f均為2.5 μm.?(x,y,λ)為響應相位,采用Pancharatnanm-Berry(PB) 相位來實現.

超透鏡的單元結構如圖2(a)所示,P為單元結構的周期,取值為0.5 μm,大約為1/(2λ) .ITO材料擁有足夠用的導電性,可以通過電焦耳加熱Sb2S3.因此通過施加適當的電流脈沖(約0.3 V),可以快速進行溫度調節,從而可以可逆調節Sb2S3的狀態.ITO 層的厚度太薄會導致加工的困難,太厚則會影響納米方柱最后的相位調控,因此綜合考慮,T取值為0.03 μm.為滿足單元結構相位的2 π 分布,Sb2S3納米方柱的高度H設置為1 μm.W和L為Sb2S3納米方柱的寬和長,可由后續優化得到.納米方柱與x軸的夾角為θ,當入射光為RCP 時,根據瓊斯矩陣的原理,單元結構的出射光場為

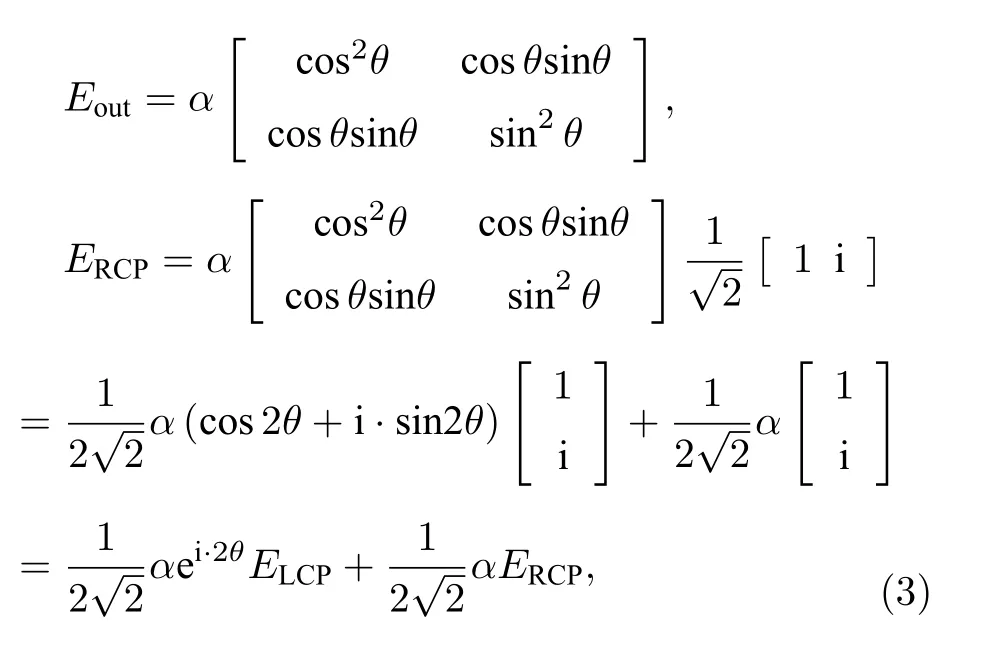
圖2 (a)單元結構的結構圖,從上至下分別是高度H 為1 μm 和不同寬度長度比W/L 的Sb2S3,厚度T 為0.03 μm 的ITO 層和SiO2基底,單元結構周期P 為0.5 μm;(b),(c) Sb2S3處于非晶態和晶態下,納米方柱不同寬度長度比W/L 的PCE 圖;(d) Sb2S3 納米方柱L=220 nm,W=160 nm 時,相位和PCE 與旋轉角 θ 的關系圖Fig.2.(a) Structural diagrams of the unit cell,from top to bottom,Sb2S3 with H of 1 μm and different W/L,ITO layer with T of 0.03 μm,and SiO2 base,and unit cell P of 0.5 μm,respectively;(b),(c) PCE diagrams of the nanosquare pillars with different W/ L when Sb2S3 is in the amorphous and crystalline states,respectively;(d) the plots of phase and PCE versus rotation angle θ for Sb2S3 nanosquare pillars with L=220 nm and W=160 nm.

其中,ERCP/LCP=表示光的偏振態,α為傳播常數.輸出光場中包含僅振幅調節的同偏振光和具有相位調制的交叉偏振光,并且納米方柱旋轉角θ與PB 相位的響應關系為θ=?/2 .Sb2S3光學相變的晶態和非晶態可以通過溫度的調控來實現可逆轉換,在1064 nm 波長下的折射率分別為3.4 和2.6,并且損耗均接近0[32].為了實現超透鏡在焦點處的可控和后續實驗中對粒子3D 捕獲的可控,Sb2S3納米方柱需要在非晶態下的偏振轉換效率(polarization conversion efficiency,PCE)最小化,因此可以選擇犧牲一點晶態下的PCE 來實現.PCE 的定義如下(入射光為RCP):

時域有限差分(finite-difference time-domain,FDTD)法可以用來對納米方柱的L和W進行參數掃描,其中L和W的變化范圍均為100—400 nm,步長為10 nm.仿真邊界均設置為周期性,最小網格單元設置為10 nm.圖2(b),(c)為Sb2S3納米方柱分別在非晶態和晶態下的PCE.最終設置納米方柱的L為220 nm,W為160 nm.圖2(d)展示了L=220 nm,W=160 nm 的納米方柱的相位和PCE 隨θ的變換.Sb2S3納米方柱在晶態和非晶態下都完全覆蓋2 π 相位分布,且滿足?=2θ.PCE與θ基本無關,且Sb2S3納米方柱在晶態下的平均PCE 約為50%,非晶態下約為10%.任何偏振未轉換的光(與入射偏振狀態相同的偏振)都不攜帶超透鏡的相位信息,對聚焦沒有任何貢獻.圖3 展示超透鏡在xz平面和xy(z=3.3 μm) 平面的電磁場強度分布圖,一共為4 個狀態.

當超透鏡A 和B 兩部分的Sb2S3均處于晶態時,會形成兩個焦點,如圖3(a),(b)所示.實際聚焦位置分別在(–4.9 μm,0,3.3 μm)和(4.9 μm,0,3.3 μm),與原設計值相差不大.焦點處的半峰全寬(full width at half maxima,FWHM)均為0.56 μm.當超透鏡只有A 部分的Sb2S3處于晶態下時,實際聚焦位置只有(–4.9 μm,0,3.3 μm),FWHM 為0.54 μm,如圖3(c),(d)所示.當超透鏡只有B 部分的 Sb2S3處于晶態下時,實際聚焦位置只有(4.9 μm,0,3.3 μm),FWHM 為0.54 μm,如圖3(e),(f)所示.當超透鏡A 和B 部分的Sb2S3均處于在非晶態下時,x方向上無焦點形成,如圖3(g),(h)所示.特別地,當z=3.3 μm,y=0 時x方向電磁場強度分布圖(圖3(a),(c),(e),(f)中的紅線所示)可以體現出,超透鏡的Sb2S3處于晶態和非晶態下焦點處強度分布最大值的對比可以達到10,實現了雙焦點的可控.

圖3 xz 平面和xy (z=3.3 μm) 平面的電磁場強度分布圖 (a),(b) A 和B 部分的Sb2S3 均處于晶態;(c),(d) A 部分的Sb2S3處于晶態,而B部分的Sb2S3處于非晶態;(e),(f) A部分的Sb2S3處于非晶態,B部分的Sb2S3處于晶態;(g),(h) A和B部分的Sb2S3 均處于非晶態Fig.3.The electromagnetic field intensity distribution in the xz plane and xy (z=3.3 μm) plane,respectively: (a),(b) Sb2S3 in both parts A and B are in crystalline state;(c),(d) Sb2S3 in part A is in crystalline state,while Sb2S3 in part B is in amorphous state;(e),(f) Sb2S3 in part A is in amorphous state,and Sb2S3 in part B is in crystalline state;(g),(h) Sb2S3 in both parts A and B are in amorphous state.

2.2 光力計算

由于本仿真實驗選取的粒子尺寸小于波長,因此光力模擬采用電磁理論中的瑞利模型進行分析[33,34].光力的數值計算是通過麥克斯韋應力張量(Maxwell stress tensor,MST)在SiO2粒子表面的虛擬閉合曲面s上進行積分求得.其中光力F計算公式如下:

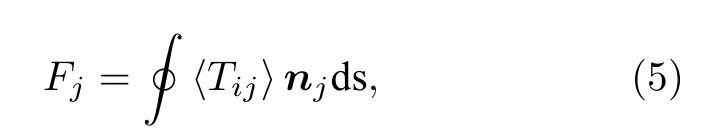
其中n為法向量,s為SiO2粒子的表面積,Tij為MST.

其中,ε和μ是常數項,分別表示真空介電常數和磁導率,E和H為電場和磁場均通過FDTD 方法求解得到.?代表共軛復數.i和j均可取x,y和z三個方向,δij為Kronecker 函數.因此Tij可以在x,y和z三個方向上展開:

光阱剛度k主要用來評估對粒子捕獲的穩定性并通過以下公式計算[35]:

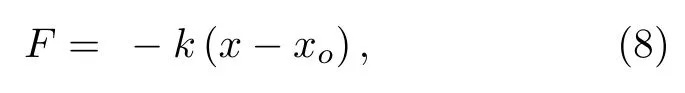
其中,F為光力,這里取最大F計算,x為當F為最大值時粒子的位置,xo為平衡點位置.光力沿其捕獲方向上的位移積分可以用勢阱深度U來表示,同樣可以用來評估對粒子捕獲的穩定:

其中,F為光力,x為粒子位置.這里采用FDTD方法對基于光學相變和超透鏡的雙阱光鑷進行仿真并驗證其對粒子3D 捕獲的可控效果.捕獲環境為空氣(n=1),入射光功率保持在100 mW.圖4展示了在超透鏡的4 種聚焦狀態下,兩個半徑250 nm 的SiO2粒子在(–4.9 μm,0,3.3 μm)和(4.9 μm,0,3.3 μm)周圍受到的橫向光力Fx和軸向光力Fz.其中藍色代表超透鏡的Sb2S3在非晶態下,SiO2粒子受到的光力大小與x方向位移和z方向位移關系,紅色代表超透鏡的Sb2S3在晶態下,SiO2粒子受到的光力大小與x方向位移和z方向位移的關系.

當A 和B 兩部分的Sb2S3均處于晶態時,兩個SiO2粒子在不同焦點處的Fx和Fz分布如圖4(a1),(a2)狀態1 所示.A 部分粒子受到的最大Fx和kx約為0.77 pN 和25.7 pN/(μm·W),B 部分粒子受到的最大Fx和kx約為0.86 pN 和37.4 pN/(μm·W).此外,Fz在z方向上的分布不對稱,這是由于z方向上焦點強度分布不均勻導致的.兩個粒子受到的最大和最小Fz均分別約為0.60 pN 和0.22 pN,kz均 約 為10.0 pN/(μm·W),因此可以實現兩個SiO2粒子在不同的焦點處穩定的3D 捕獲.當A 部分的Sb2S3處于晶態,B 部分的Sb2S3處于非晶態時,兩個SiO2粒子在不同焦點處的Fx和Fz分布如圖4(b1)和圖4(b2) 狀態2 所示.A 部分粒子的Fx和Fz與其狀態1 中基本一致,可以實現對粒子的3D 捕獲.而B 部分的最大Fx和kx約為0.08 pN 和4 pN/(μm·W),最大和最小Fz約為0.08 pN 和0.01 pN,kz約為0.69 pN/(μm·W),均約為其晶態下的1/10,并且其最小Fz也遠小于最大Fz,并更接近0,因此粒子在z方向的捕獲是不穩定的.這主要是因為,在非晶態條件下,焦點處的光強分布不均勻導致粒子所受的散射力遠大于梯度力而引起的.當B 部分的Sb2S3處于晶態,A 部分的Sb2S3處于非晶態時,兩個SiO2粒子在不同焦點處的Fx和Fz分布如圖4(c1),(c2)狀態3 所示.B 部分粒子的Fx和Fz與其狀態1 中基本保持一致,可以實現粒子穩定的3D 捕獲.而A 部分的最大Fx和kx約為0.06 pN 和2.0 pN/(μm·W),最大和最小的Fz約為0.06 pN 和0.01 pN,kz均約為0.69 pN/(μm·W),均約為其晶態下的1/10,同樣其最小Fz遠小于最大Fz并更接近0,從而不能實現對SiO2粒子的穩定的3D 捕獲.當A 和B 部分的Sb2S3均處于非晶態時如圖4(d1),(d2)狀態4 所示,A 和B 兩部分粒子受到的Fx和最大Fz分別與其在狀態3 和2 中保持一致,但是最小Fz進一步減小至0.006 pN,這主要是由于A 和B部分的入射光均基本不能透過,焦點處光強減弱導致的.此外,z方向的光強分布不均勻,最終會使得兩個SiO2粒子在z方向上完全不能被捕獲.此外,半徑為250 nm 的SiO2粒子重量約為7.9×10–4pN,遠遠小于Sb2S3為晶態時粒子受到的正方向最大Fz.因此,z軸的光力是可以平衡重力的.從4 個狀態可以看出,基于光學相變和超透鏡的雙阱光鑷實現了對粒子的可控3D 捕獲.并且,A 和B 兩個部分是獨立的,基本不互相影響,因此可以通過單獨調節超透鏡每個部分的Sb2S3狀態來實現不用方式的粒子捕獲.

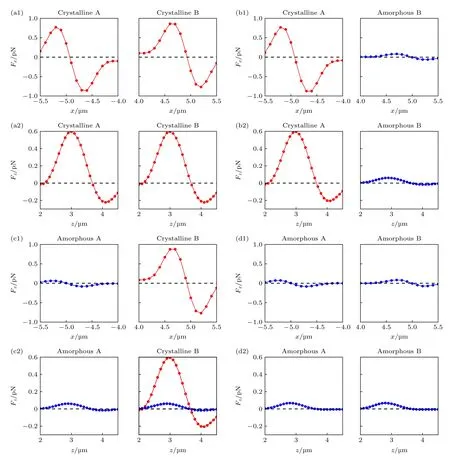
圖4 施加在粒子上Fx 和Fz 分別與x 位移和z 位移的關系圖 (a) A 和B 部分的Sb2S3 均處于晶態;(b) A 部分的Sb2S3 處于晶態,而B 部分的Sb2S3 處于非晶態;(c) A 部分的Sb2S3 處于非晶態,B 部分的Sb2S3 處于晶態;(d) A 和B 部分的Sb2S3 均處于非晶態Fig.4.Plots of Fx and Fz for the particle versus x displacement and z displacement,respectively: (a) Sb2S3 in both parts A and B are in crystalline state;(b) Sb2S3 in part A is in crystalline state,while Sb2S3 in part B is in amorphous state;(c) Sb2S3 in part A is in amorphous state,and Sb2S3 in part B is in crystalline state;(d) Sb2S3 in both parts A and B are in amorphous state.

由于圖3 中顯示的電磁場強度分布在y向相較于x有明顯的拉伸,因此本文又分析了A 和B 部分在Sb2S3晶態和非晶態下SiO2粒子受到的Fy與y方向位移的關系.在圖5(a)中,當A 部分的Sb2S3處于晶態時,最大Fy和ky約為0.77 pN和11 pN/(μm·W),平衡點為(–4.97 μm,–0.34 μm,3.6 μm);而當Sb2S3處于非晶態時,最大Fy和ky約為0.07 pN 和0.8 pN/(μm·W),均約為晶態下的1/10.圖5(b)顯示,當B 部分的Sb2S3處于晶態時,最大Fy和ky約為0.76 pN 和10.9 pN/(μm·W),平衡點為(4.97 μm,0.34 μm,3.6 μm);而當Sb2S3處于非晶態時,最大Fy和ky分別約為0.07 pN 和0.7 pN/(μm·W),均約為晶態下的1/10.其中,Fy在y方向上的分布不對稱,是由于y方向上的焦點強度分布不均勻導致的.由于用于雙阱光鑷的超透鏡在設計時候的焦點位置偏離超透鏡的中心位置(0,0),從而使得聚焦光束向設計的焦點位置發生偏斜(圖3 中xz平面的電磁場強度分布圖也有體現),導致在3 個方向上焦點強度分布不均勻.

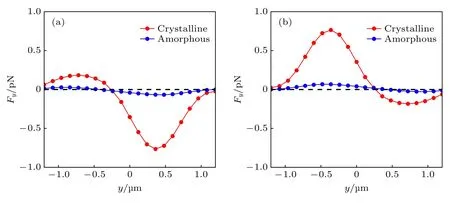
圖5 施加在粒子上Fy 與y 位移關系圖 (a) A 部分的Sb2S3 分別均處于晶態和非晶態;(b) B 部分的Sb2S3 分別均處于晶態和非晶態Fig.5.Plots of Fy for the particle versus y displacement: (a) Sb2S3 in part A is in the crystalline and amorphous states,respectively;(b) Sb2S3 in part A is in the crystalline and amorphous states,respectively.

本文進一步計算了超透鏡A 和B 部分的Sb2S3處于晶態下的勢阱深度U,并與kBT進行歸一化,其中kB為玻爾茲曼常數(1.38×10–23J/K),T為溫度(300 K)[36].圖6 顯示了超透鏡A 和B 部分在晶態下的Ux和Uz.

圖6 當A 和B 部分的Sb2S3 為晶態時Fx 和Fz 的勢阱深度圖 (a),(b) Fx 的勢阱深度Ux 圖;(c),(d) Fz 的勢阱深度Uz 圖Fig.6.Potential depth plots of Fx and Fz when parts A and B are crystalline state: (a),(b) potential depth Ux plots of Fx;(c),(d) potential depth Uz plots of Fz.

圖6(a),(b)為超透鏡A 和B 部分Fx的勢阱深度.平衡點處為最大勢阱深度,A 和B 部分的最大Ux分別為68.3× kBT和96.4× kBT,圖6(c),(d)為超透鏡A 和B 部分Fz的勢阱深度,Uz均為123.0× kBT.其中,所有的勢阱深度值都遠遠大于kBT,表明在用于雙阱光鑷的超透鏡中,當A 和B 部分的Sb2S3處于晶態下時,可以實現粒子的穩定3D 捕獲.值得注意的是,A 和B 部分的最大Ux的不同是由于xy平面上焦點處的電磁場強度分布存在較小的不對稱,使得B 部分沿正方向的最大Fx(0.86 pN)要大于A 部分沿正方向的最大Fx(0.77 pN).此外B 部分粒子朝正方向的運動位移要大于A 部分的粒子,因此根據 (9)式勢阱深度的計算方式,B 部分的最大Ux要大于A 部分.

3 基于光學相變和超透鏡的可控多阱光鑷

為了進一步提高光鑷系統的高效性,本文設計了基于相變材料Sb2S3,且直徑為30 μ m 的超透鏡,并用于可控多阱光鑷,其設計思路與實現雙阱光鑷的基本相同.超透鏡被分為9 個部分,每個部分的相位分布公式如下:

其中,i代表超透鏡9 個部分,λ和f同樣取值為1064 nm 和2.5 μm.同樣,當每個部分的Sb2S3處于紅色晶態時,形成焦點,當Sb2S3處于藍色非晶態時,則無焦點形成,如圖7(a),(b)所示.并且超透鏡的入射光為RCP,出射光為LCP.

圖7(a)顯示了當超透鏡中間部分的Sb2S3處于非晶態,其余部分的Sb2S3均處于晶態時的結構圖.圖7(c),(d)則顯示了其在xy(z=3.3 μm)平面和xz平面上的強度分布圖.可以看出在xy平面上紅色虛框里的焦斑強度明顯小于周圍的焦斑.在xz平面上,焦點的實際位置在z=3.3 μm,與設計位置相差不大,FWHM 為0.62 μm.特別地,晶態和非晶態下的焦點處強度分布的最大值的對比可以達到10,實現了焦點形成和消失的可控.圖7(b)顯示了所有部分的Sb2S3均處于晶態下的結構圖,相對應的xy(z=3.3 μm)和xz強度分布圖如圖7(e),(f)所示.超透鏡所有部分均形成焦點,并且FWHM 相差不大,分別為0.56,0.64 和0.56 μm.

圖7 (a),(b) 用于多阱光鑷的超透鏡結構圖,(a) 中間部分的Sb2S3 處于非晶態,其余部分的Sb2S3 均處于晶態,(b)所有部分的Sb2S3 均處于晶態;(c),(d) 分別為(a)狀態下xy (z=3.3 μm)平面和xz 平面的電磁場強度分布圖;(e),(f) 分別為(b)狀態下xy (z=3.3 μm)平面和xz 平面的電磁場強度分布圖Fig.7.(a),(b) Structure of the multi-trap optical tweezer metalens,(a) Sb2S3 in the middle part is in the amorphous state,and Sb2S3 in the rest parts are in the crystalline state,(b) Sb2S3 in all parts are in the crystalline state;(c),(d) the electromagnetic field intensity distributions in the xy (z=3.3 μm) plane and xz plane in (a) state,respectively;(e),(f) the electromagnetic field intensity distributions of xy (z=3.3 μm) plane and xz plane in (b) state,respectively.

隨后本文討論了圖7(c)和圖7(e)中紅色虛線對應部分的Sb2S3在晶態和非晶態下,半徑為0.25 μm 的SiO2粒子受到的Fx和Fz分別與x位移和z位移的關系,如圖8(a),(b)所示.圖8(a)為SiO2粒子受到的Fx與x位移的關系.晶態下,SiO2粒子受到的最大Fx和kx分別為0.6 pN 和20 pN/(μm·W),而非晶態下的最大Fx和kx分別為0.04 pN 和1.3 pN/(μm·W),僅約為其晶態下的1/10,因此,微球的橫向穩定性較弱.圖8(b)為SiO2粒子受到Fz與z位移的關系.晶態下,SiO2粒子受到的最大和最小Fz分別為0.49 和0.05 pN,kz為3 pN/(μm·W),平衡點為(0,0,5.1 μm),根據上述計算的SiO2粒子的重力,z軸的光力也是可以平衡重力的.非晶態下,SiO2粒子受到的最大和最小Fz分別為0.06 和0.007 pN,kz=0.3 pN/(μm·W),均約為晶態下的1/10.并且,由于焦點位置處的光強分布不均勻,導致散射力遠大于梯度力,因此最小Fz約為最大Fz的1/10,基本趨近于0,因此粒子在z方向上完全不能被穩定捕獲.由此可見,超透鏡的中間部分可以實現對粒子的可控3D 捕獲.圖8(c),(d)為中間部分的Sb2S3處于晶態時Fx和Fz的勢阱深度,Ux和Uz的最大勢阱深度分別為64.2× kBT和153.9× kBT,證明可以實現粒子穩定的3D 捕獲.因此可以推廣到超透鏡的其他8 個部分,實現同時對多個粒子的可控3D 捕獲.

基于上述用于多阱光鑷對粒子的可控3D 捕獲的理論與仿真分析,可以實現同時操縱和捕獲多個SiO2粒子并擺放成任意的圖案.圖9 展示了超透鏡在6 種聚焦狀態下的xy(z=3.3 μm)平面和xz平面的強度分布圖.其中,超透鏡中的每一部分都可以控制Sb2S3晶態和非晶態的轉換,并實現對粒子的可控3D 捕獲.因此本文可以僅通過使用同一個超透鏡便可實現多種方式的粒子捕獲并形成多種形狀的圖案,進一步提高了光鑷的高效性.

目前基于相變材料Sb2S3的超透鏡加工可以采用電子束光刻和反應離子刻蝕對Sb2S3薄膜進行圖案化[37,38].其中,超透鏡采用SiO2蓋層,頂部是導電的碳層.Sb2S3薄膜可以通過原位襯底加熱下的離子濺射而產生,過量的硫可以通過提高襯底溫度和非原位退火來緩解[37,38].ITO 層可以濺射在SiO2襯底上[39].對于雙焦點和多焦點的超透鏡設計,每一個區域之間可以添加薄的絕緣體材料,這樣便可以避免熱傳導[40],從而實現對不同區域的狀態調控.

4 結論

本文首先設計了基于低損相變材料Sb2S3和超透鏡的可控雙阱光鑷.其中,超透鏡被分為兩個部分: Sb2S3均處于晶態下時,A 部分粒子受到的最大Fx和kx分別約為0.77 pN 和25.7 pN/(μm·W),B 部分粒子受到的最大Fx和kx分別均約為0.86 pN和37.4 pN/(μm·W),兩部分粒子的最大和最小Fz均分別約為0.60 pN 和0.22 pN,kz均約為10.0 pN/(μm·W),都約是其非晶態下的10 倍,實現了對粒子穩定的3D 捕獲.其中,在非晶態下由于光強分布不均勻,粒子的最小Fz均小于最大Fz并更接近0,因此在z 方向容易被光“推走”,從而不能實現粒子穩定3D 捕獲.在此基礎上,為進一步增加光鑷系統捕獲性能的高效性,本文設計了基于相變材料Sb2S3和超透鏡的可控多阱光鑷.其中,當超透鏡中間部分的Sb2S3為晶態時,最大的Fx和Fz分別為0.6 pN 和0.49 pN,kx和kz分別為20 pN/(μm·W)和3 pN/(μm·W),均約是其非晶態下的10 倍,同樣可以實現粒子的可控3D 捕獲.因此可以擴展到超透鏡的其他部分實現多種粒子的可控3D 捕獲并形成多種形狀的陣列.可控3D 捕獲增加了超透鏡光鑷系統的高效性和靈活性,可以僅通過單一的超透鏡來實現粒子的不同捕獲狀態,提高了光鑷的實用性,并提供了一種新的超透鏡光鑷的設計思路.