基于最小二乘法和支持向量機的海洋內孤立波傳播速度反演模型*

梁可達 劉滕飛 常哲 張猛 李志鑫 黃松松 王晶

(中國海洋大學物理與光電工程學院,青島 266100)

傳播速度是內孤立波的重要參數之一,如何通過光學遙感圖像準確快速地獲得內孤立波速度是目前需要解決的重要科學問題.本文在實驗室建立了模擬內孤立波光學遙感成像系統,開展了系列綜合實驗,獲取實驗數據庫,并利用最小二乘法和支持向量機兩種方法分別建立基于單景光學遙感圖像的內孤立波速度反演模型.利用中國南海的MODIS 圖像和GF-4 圖像數據對速度反演模型進行精度檢驗.研究結果表明: 最小二乘法內孤立波速度反演模型能夠給出回歸方程,物理意義更為直觀,且在300—399 m 水深范圍精度更高,而支持向量機內孤立波速度反演模型在水深400—1200 m 和83—299 m 的范圍內精度高.因此兩種內孤立波速度反演模型各有優勢,都可以應用于真實海洋中內孤立波速度的反演.

1 引言

海洋內波是指在海水穩定層化的海洋中產生的、最大振幅出現在海洋內部的波動,是一種常見的海洋現象[1].海洋內孤立波是周期短的非線性內波,具有傳播的單向性和波形的不變性等特點[2].海洋內孤立波會對海上石油、天然氣等資源的勘探以及開采設施的安全構成破壞,也會改變水下聲信號傳播路線,對潛艇航行產生影響等等[3?6].同時海洋內孤立波會影響海洋表面溫度的變化[7],對海洋的生態環境具有重要影響[8].因此,研究內孤立波特性具有重要的科學意義和良好的應用前景.

目前研究內孤立波的方法有很多,其中利用衛星遙感圖像是研究內孤立波的重要方法之一[9,10].其中光學遙感具有時間、空間分辨率較高和圖像豐富等優點,常被學者用來研究內孤立波的時空分布及傳播特性[11?13].海洋內孤立波的特征參量主要包括半寬、振幅和速度等,這些參量的大小決定了內孤立波在海洋混合中的作用量級,因此遙感圖像反演內孤立波參數引起了研究人員的關注.而內孤立波的速度作為重要的傳播特性,一直以來也被許多學者利用不同手段開展研究.目前測量內孤立波傳播速度的常用方法主要是通過現場實測或利用遙感圖像計算內孤立波速度.現場實測可以通過兩個或多個系泊裝置觀測內孤立波計算傳播速度,該方法難度大、費用昂貴.Alford[14]等利用2007 年的系泊數據研究了中國南海的非線性內波的速度和演化.Huang 等[15]利用水下系泊陣列進行了“南海內波實驗”.報道了2013 年12 月4 日的一次極端內孤立波,其最大振幅為240 m,并對傳播速度進行了分析.此外,呂海濱等[16]利用 2009 年 6 月24 日 15 時 40 分至 25 日 16 時 40 分“科學一號”考察船在東沙島東北部陸架上K106 站進行的長達 25 h 的 X 波段雷達、溫度鏈、聲學多普勒流速剖面儀同步觀測,在該海域利用 Radon 變換技術獲取了本次觀測到的內孤立波的傳播速度.雖然現場實測可以測量內孤立波平均速度,但大規模大范圍的測量難于實現.

遙感觀測手段測量內孤立波速度主要是利用多時間圖像法,即采用同一天不同時刻的包含同一內孤立波的遙感圖像,利用傳播路程與傳播時間的比值估算內孤立波的傳播速度.Hong 等[17]利用衛星數據估算南海淺水區內孤立波相速度,基于環境衛星高級合成孔徑雷達(ASAR)和中分辨率成像光譜儀(MODIS)在很短的時間間隔獲得不同的位置圖像,進行內孤立波速度計算.Meetei 等[18]利用2002 年12 月 至2016 年5 月 的ERS2 和Envi Sat 衛星的不同圖像對和MODIS 的光學圖像,以及可見紅外成像輻射計來調查和估計安達曼海內孤立波的傳播速度.Sun 等[19]利用MODIS Terra/Aqua 衛星2014 年1 月至2018 年12 月采集的195對影像對估算安達曼海內孤立波傳播速度.多時間圖像法計算內孤立波速度相比現場實測手段更加便捷,但很難獲取某一海域任意時刻的兩景包含同一內孤立波的光學遙感圖像,且該方法計算的速度為內孤立波平均速度，這些都是該方法的不足之處.然而,發展一種只用單景圖像反演內孤立波速度的方法顯然是非常重要的.

本文通過實驗模擬光學遙感內孤立波成像,獲得了大量實驗數據,采用最小二乘法和支持向量回歸兩種方法建立利用單景光學遙感圖像反演內孤立波速度的模型,為內孤立波速度的研究和獲取提供了新方法.無疑,這對于海洋內孤立波傳播特性的研究起到了推動作用.

2 實驗設計及數據處理

2.1 實驗設計

實驗在長寬高分別為5 m×0.8 m×0.35 m 三維長直水槽中進行.為模擬海洋中的層結現象,根據流體力學相似性原理,在水槽中鋪設上下兩層水體,下層水體模擬高鹽度海水,上層水體模擬低鹽度海水.長直水槽為玻璃材質,可從水槽側面觀測水體內部的內孤立波演化過程,從而獲取內孤立波的半波寬度、振幅和速度等參數.為了仿真光學遙感成像,將水槽中的水體表面視為海表面,在水槽一端上方放置LED 面光源,調整好角度,發出白光模擬太陽光;在水槽另一端上方放置CCD1,模擬衛星的可見光傳感器,LED 光源發出的光照射到水體表面,經反射后在CCD1 形成仿真光學遙感內孤立波圖像;在水槽側面放置CCD2,與上下層水體的分層位置等高,用來采集記錄內孤立波圖像,獲取內孤立波特征參量.兩臺CCD 的視場邊界相同,并連接一臺電腦同步采集圖像,獲得了內孤立波一一對應的仿真光學遙感圖像和波形圖像,光學遙感圖像參數與內孤立波特征參數完全匹配[20].實驗平臺結構如圖1 所示.

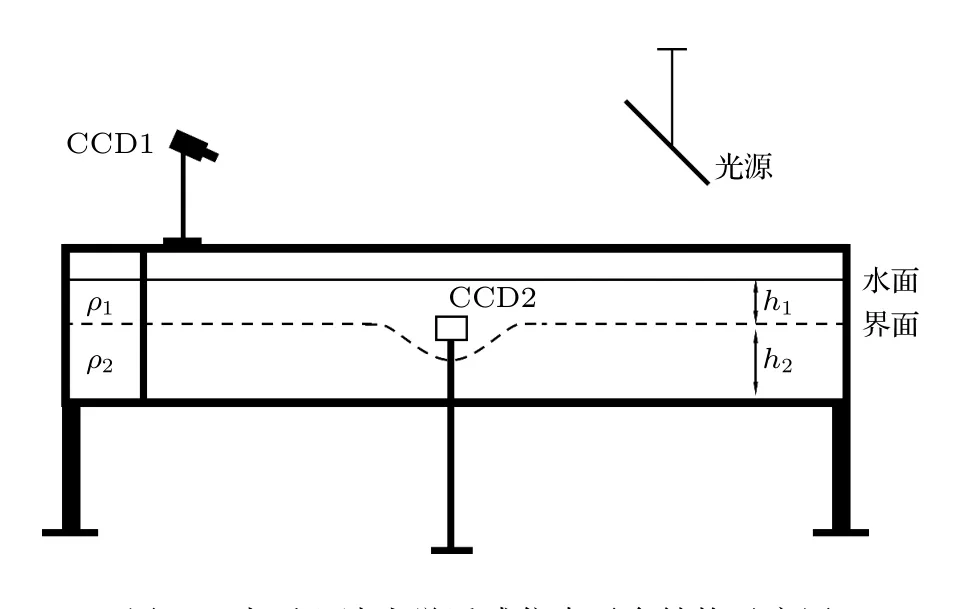
圖1 內孤立波光學遙感仿真平臺結構示意圖Fig.1.Schematic diagram of simulation platform of the internal solitary wave optical remote sensing.

實驗采用重力塌陷法制造內孤立波,即靠近水槽一側用擋板隔開的區域為造波區,可以通過控制在造波區加入或抽取上層水體的多少來控制塌陷高度,獲得內孤立波不同大小的振幅.針對不同水文參數和層結的海洋,根據流體力學相似性原理設計了不同水深、不同層結、不同密度差和不同塌陷高度的系列實驗,如表1 所列.

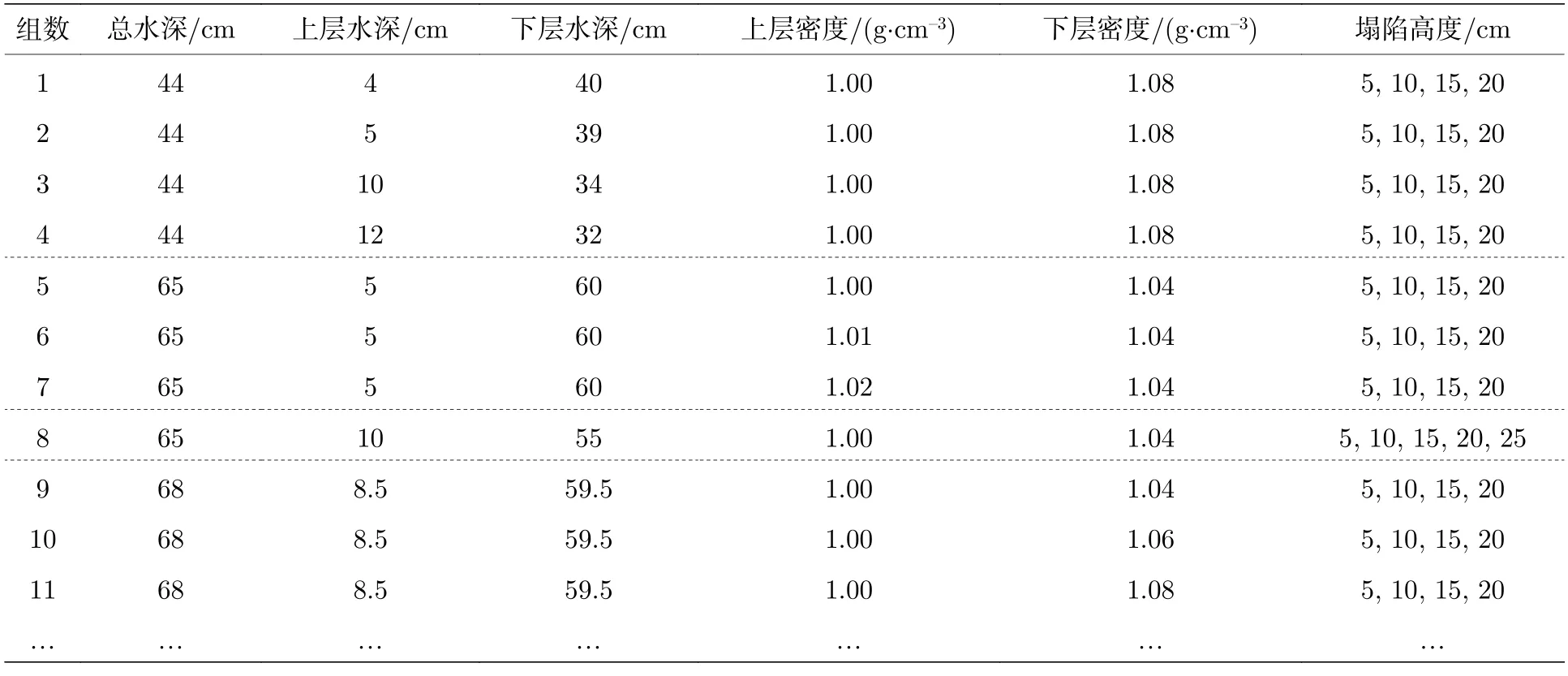
表1 內孤立波實驗設計表Table 1.Design table of internal solitary wave experiment.

2.2 數據處理

在采集的圖像中選取不同位置做時間序列圖,CCD1 采集圖像的時間序列圖模擬了光學遙感圖像,可從中提取亮暗間距和灰度差等遙感圖像特征參量.CCD2 采集圖像的時間序列圖可提取內孤立波傳播速度、半波寬度和振幅等波要素參量.在提取同一組實驗的參數時,根據標尺選取表面與側面圖像相對應的取樣線,利用MATLAB 程序做時間序列圖,如圖2 所示.圖2(a)為內孤立波仿真光學遙感圖像,圖2(b)為內孤立波波形圖,可提取內孤立波振幅、半波寬度等參數,圖2(c)為內孤立波仿真光學遙感圖像灰度剖面圖,可提取灰度差和亮暗間距等遙感圖像參數.

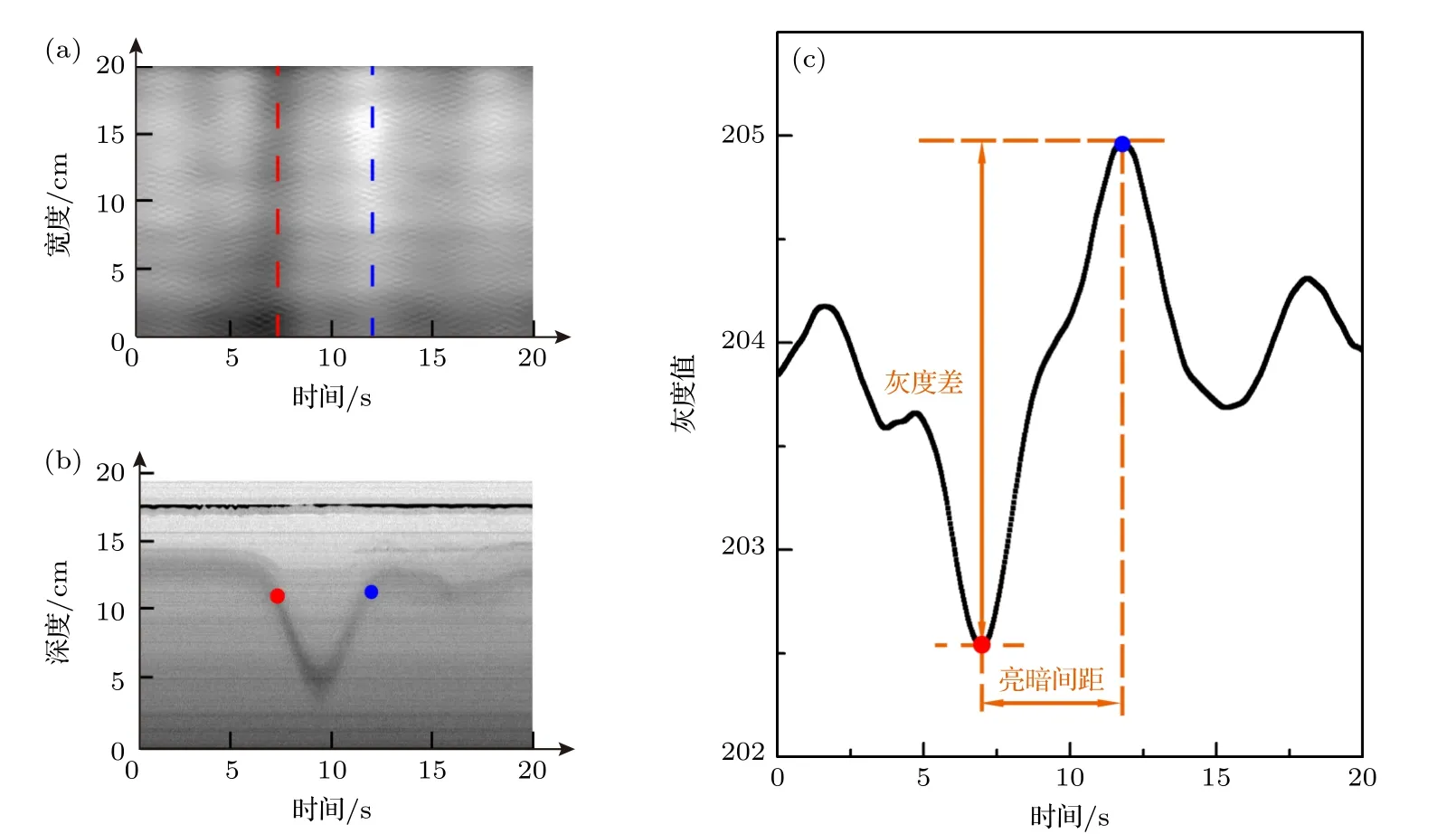
圖2 實驗室內孤立波參數示意圖 (a) 內孤立波仿真遙感圖像;(b)內孤立波波形圖;(c)內孤立波灰度剖面圖Fig.2.Schematic diagram of the internal solitary wave parameters in the laboratory: (a) Simulated remote sensing images;(b) the internal solitary wave waveform diagram;(c) the gray scale profiles.

在實驗中共提取1440 組實驗數據,每組實驗數據包括上下層水深、上下層密度、振幅、速度、半波寬度、亮暗間距、灰度差等參數.對獲得的1440 條實驗數據進行無量綱化處理,無量綱參量定義如下:

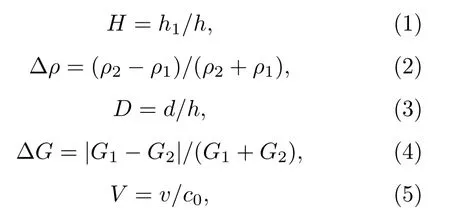
h1,h分別為水槽實驗的上層水深和總水深,ρ1,ρ2分別為上層和下層水的密度,d,G1,G2分別為仿真遙感圖像內孤立波條紋的亮暗間距、灰度最大值和灰度最小值,v為內孤立波傳播速度,c0為線性相速度.建立了無量綱化的實驗室內孤立波數據樣本庫,利用樣本庫中的數據進行內孤立波速度反演模型的訓練.

3 內孤立波速度反演模型

從經典的KdV 理論模型中可知內孤立波傳播速度與水深、層結、密度差和振幅相關,對于海洋內孤立波的振幅可以通過現場實測和光學遙感圖像反演模型獲取,Wang 等[21]利用內孤立波光學遙感圖像中條紋的灰度差和亮暗間距以及其他海洋水文參數反演了內孤立波振幅.而本文是利用光學遙感圖像來進行內孤立波速度的反演,所以輸入參量中包含了與內孤立波振幅相關的光學遙感圖像特征參量亮暗間距和灰度差,以這兩項遙感圖像參數反映內孤立波振幅的作用.因此建立內孤立波速度反演模型時將水深、水體分層結構、密度差和遙感圖像的亮暗間距、灰度差作為速度反演模型的自變量.下文分別利用最小二乘法和機器學習兩種技術建立內孤立波速度反演模型.

3.1 最小二乘法的內孤立波速度反演模型

最小二乘法是解決曲線擬合的常用方法,其原理是尋找最小化的誤差平方和來確定與數據對應的最佳匹配函數,進而可以直觀表達因變量與自變量的函數關系,物理意義也就一目了然,所以最小二乘法在多個領域研究中被廣泛地應用.本文利用所獲得的大量內孤立波實驗數據,采用最小二乘法尋找最佳的回歸方程,建立基于最小二乘法的反演內孤立波速度模型.將無量綱數據庫中的H,△ρ,D,△G作為模型自變量,將V作為因變量.考慮到4 個自變量是相互獨立的,所以在回歸方程中將其作為獨立項進行擬合.由KdV 方程等理論可知速度與自變量具有非線性關系,回歸方程中應包含有自變量的高次方項.因此通過最小二乘法擬合的二次回歸方程和三次回歸方程如下:

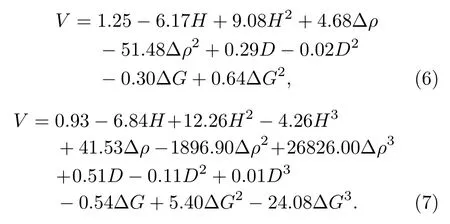
用實驗數據檢驗回歸方程反演值的結果如圖3 所示,圖3(a)為2 次方的回歸方程的結果,方程反演值與實驗值的相關系數為0.927,平均絕對誤差為1.64 cm/s,平均相對誤差為8.25%.圖3(b)為最高次為3 次方的回歸方程的結果,方程反演值與實驗值的相關系數為0.928,平均絕對誤差為1.61 cm/s,平均相對誤差為8.13%.從圖中可知,2 個回歸方程都有效,它們的相關系數和誤差大小接近,差異不大.

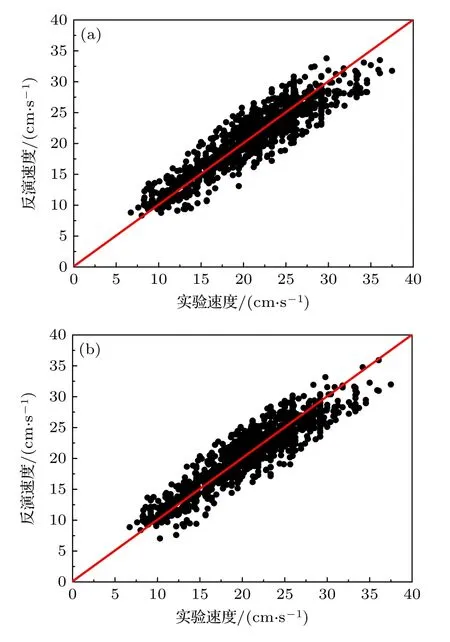
圖3 最小二乘法回歸方程反演結果散點圖 (a)最高冪次為2 次方;(b)最高冪次為3 次方Fig.3.Scatter plot of the inversion results of the least squares regression equation: (a) With the highest power of 2;(b) with the highest power of 3.

3.2 支持向量回歸內孤立波速度反演模型

支持向量機中的支持向量回歸(support vector regression,SVR)是一種應用于函數回歸預測領域的機器學習方法,SVR 相較于其他機器學習方法而言更適合于小樣本的回歸預測,且能夠處理樣本數據線性不可分的情況,所以本文采用SVR 的方法對內孤立波速度反演模型進行訓練.選擇局部性強且有將訓練樣本的特征空間從低維映射到無窮維性能的高斯徑向基函數(radial basis function,RBF)作為模型核函數.

與最小二乘法相同,將無量綱數據庫中的H,Δρ,D,ΔG作為模型輸入參量,將V/C0作為輸出參量.首先將所有數據輸入SVR 程序中運行,去除誤差較大的數據后,將剩余的1383 條樣本數據隨機排序,按照大致4∶1 的比例劃分為模型訓練集和測試集,訓練集為1100 條樣本數據,測試集為283 條樣本數據.之后再次將數據輸入SVR程序進行模型訓練,得到模型后,記錄模型的懲罰系數c和核函數參數g的值,c的值為1,g的值為16.圖4 為SVR 內孤立波速度反演模型測試集實驗數據與反演數據散點圖,反演值與實驗值的相關系數為0.888,平均絕對誤差為2.10 cm/s,平均相對誤差為10.28%,表明模型是有效的.

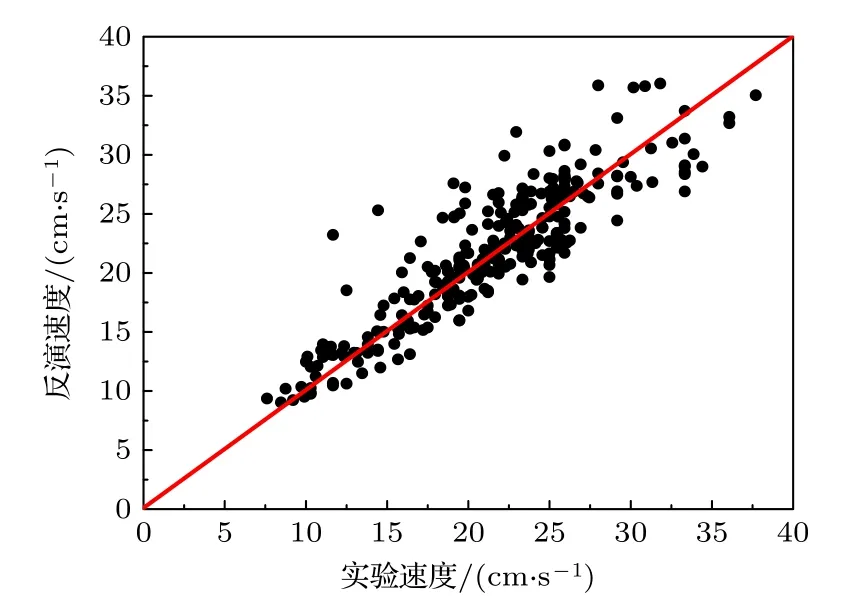
圖4 SVR 內孤立波速度反演模型測試集散點圖Fig.4.Scatter plot of test set of solitary wave speed inversion model in SVR.

4 結果與分析

4.1 光學遙感圖像下載與處理

選取2021 年中國南海海域的遙感圖像和數據來進行模型精度驗證,在NASA 官方遙感影像數據下載網站LADDS DAAC 下載所需的MODIS遙感圖像,在中國資源衛星應用中心下載高分4 號衛星光學遙感圖像.對遙感圖像進行篩選和處理,提取參數,對模型精度進行驗證.

采用多時間圖像法對內孤立波速度進行計算,從獲得有內孤立波的遙感圖像中選取同一天不同時刻的圖像,找到同一個內孤立波,根據不同遙感圖像中的內孤立波位置計算其傳播距離,兩景遙感圖像的間隔時間為內孤立波的傳播時間,傳播距離與傳播時間的比值就是傳播速度.同時利用ENVI軟件提取內孤立波的亮暗間距和灰度差等遙感圖像參數.圖5 為多時間圖像法示意圖.一般在采用多時間圖像法計算內孤立波傳播速度時兩景圖像的時間間隔約在1—3 h,時間間隔較短,所以將計算的平均速度近似作為兩景遙感圖像中內孤立波的傳播速度.

圖5 多時間圖像法示意圖 (a) 2021年5月25日10:43南海海域GF4光學遙感圖像;(b) 2021年5月25日13:40南海海域MODIS 光學遙感圖像Fig.5.Schematic diagram of the multi-time image method: (a) An optical remote sensing image of GF-4 in the South China Sea at 10:43 on May 25,2021;(b) the MODIS optical remote sensing image of the South China Sea area is at 13:40 on May 25,2021.

從光學遙感圖像中提取內孤立波條紋的亮暗間距和灰度差,對數據進行無量綱化處理,將輸入參量代入反演模型,利用上述模型計算內孤立波速度.與多時間圖像法計算出的內孤立波傳播速度比較,驗證模型精度.

4.2 模型精度驗證

在利用最小二乘法內孤立波速度反演模型對遙感數據進行反演時,兩種模型的反演值均小于實測值,存在系統偏差,如圖6 中黑色散點所示.實驗仿真與真實海洋的差異可能是導致驗證時產生系統偏差的原因.為了消除系統偏差,對模型進行校正,使得系統偏差和其他誤差最小,校正后的模型如下:

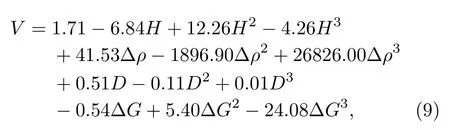
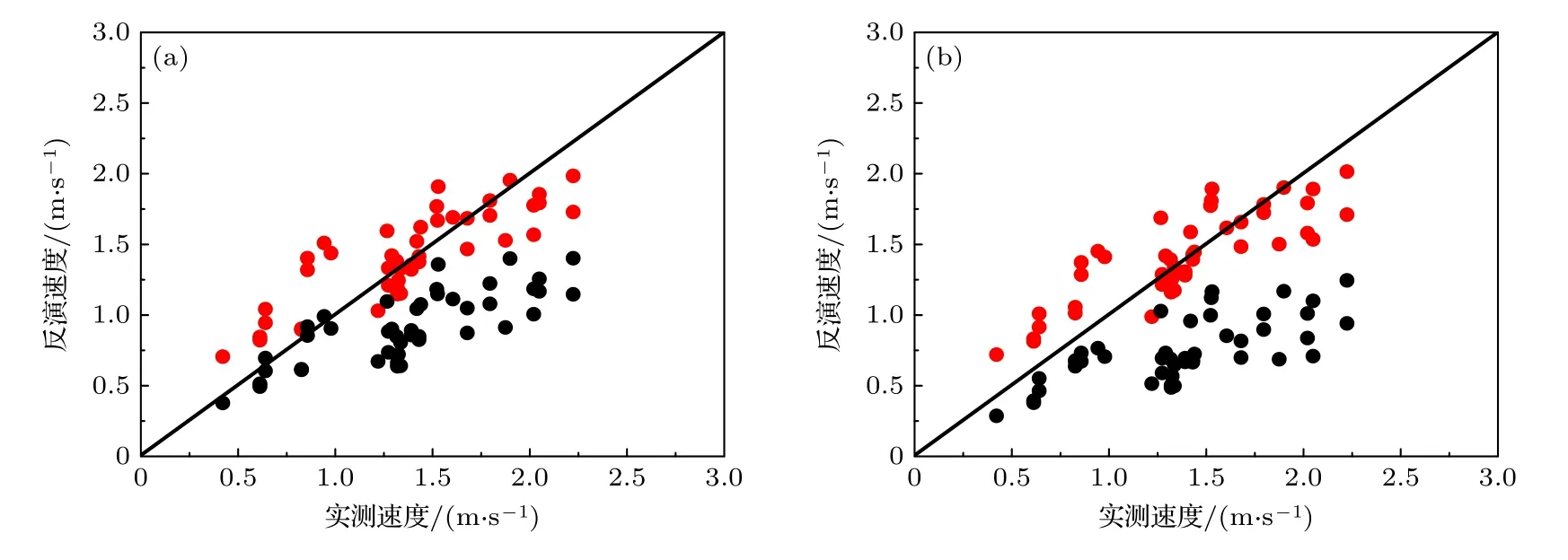
圖6 最小二乘法內孤立波速度反演模型精度散點圖 (a)校正前后最高冪次為2 次方的最小二乘法回歸方程的反演結果散點圖,黑色散點為校正前模型結果,紅色散點為校正后模型結果;(b)校正前后最高冪次為3 次方的最小二乘法回歸方程的反演結果散點圖,黑色散點為校正前模型結果,紅色散點為校正后模型結果.Fig.6.Scatter plot of the solitary wave speed inversion model accuracy within least squares.(a) The scatter plot of inversion results of least squares regression equation with the highest power of 2 before and after correction.The black scatters are the model results before correction,and the red scatters are the model results after correction.(b) The scatter plot of the inversion results of the least squares regression equation with the highest power of 3 before and after correction.The black scatters are the model results before correction,and the red scatters are the model results after correction.

(8)式為校正后的2 次方最小二乘法反演模型,常數項由1.25 校正為1.84,校正前后的實測值與反演值分別如圖6(a)中黑色散點和紅色散點所示.(9)式為校正后的3 次方最小二乘法反演模型,常數項由0.93 校正為1.71,校正前后的實測值與反演值分別如圖6(b)黑色散點和紅色散點所示.由圖6 可知,校正后的模型消除了系統偏差,反演效果良好,所以將校正后的模型作為最終模型.

依據4.1 節的方法,共獲得南海光學遙感觀測的44 個內孤立波速度數據,將所得的遙感觀測數據按水深劃分為400—1200 m,300—399 m,200—299 m 和83—199 m 四個范圍,用3 種模型對光學遙感數據進行反演.反演結果如表2 和圖7所示.

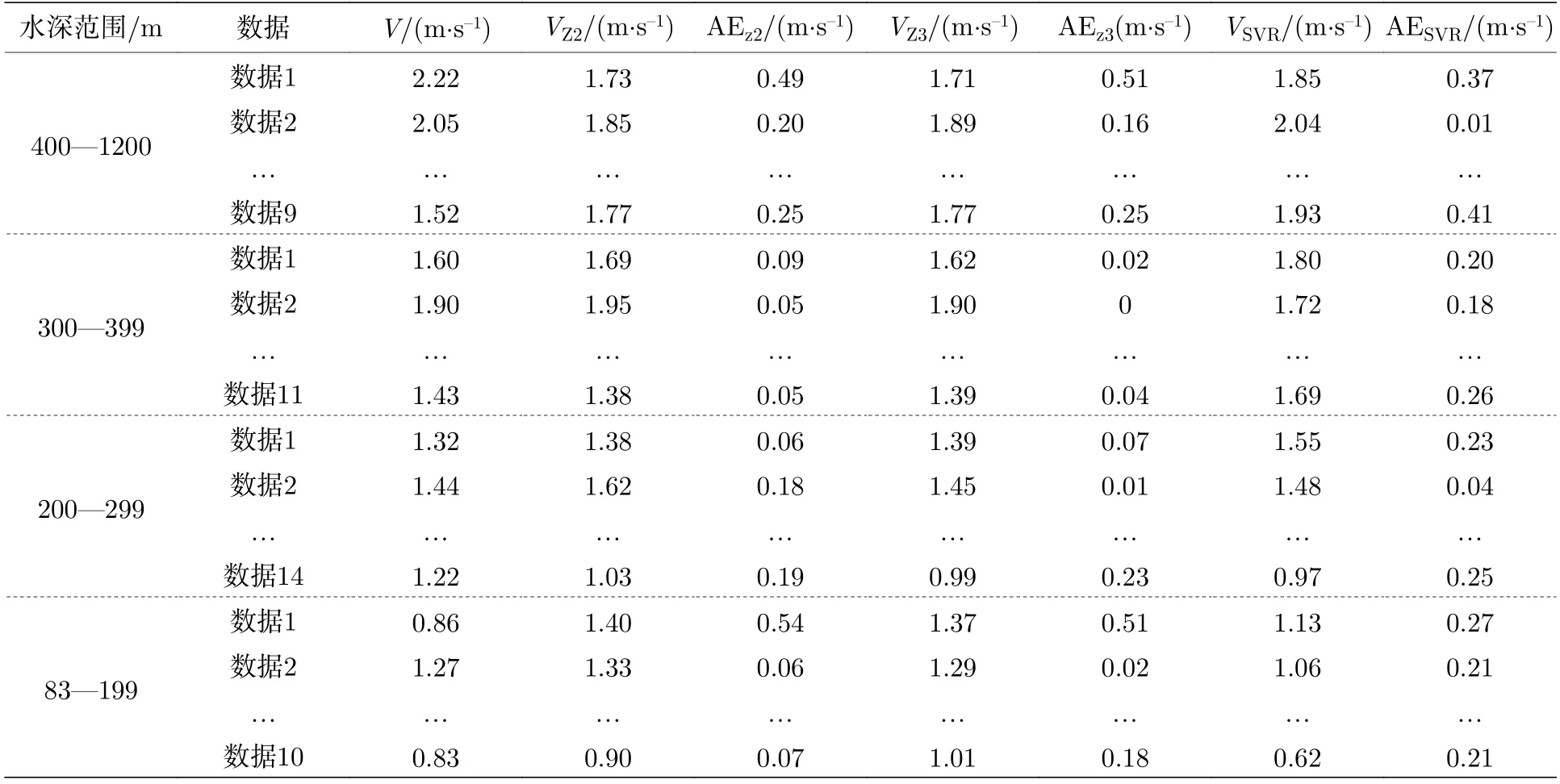
表2 內孤立波速度反演模型精度驗證表Table 2.Precision verification table of internal solitary wave velocity inversion model.

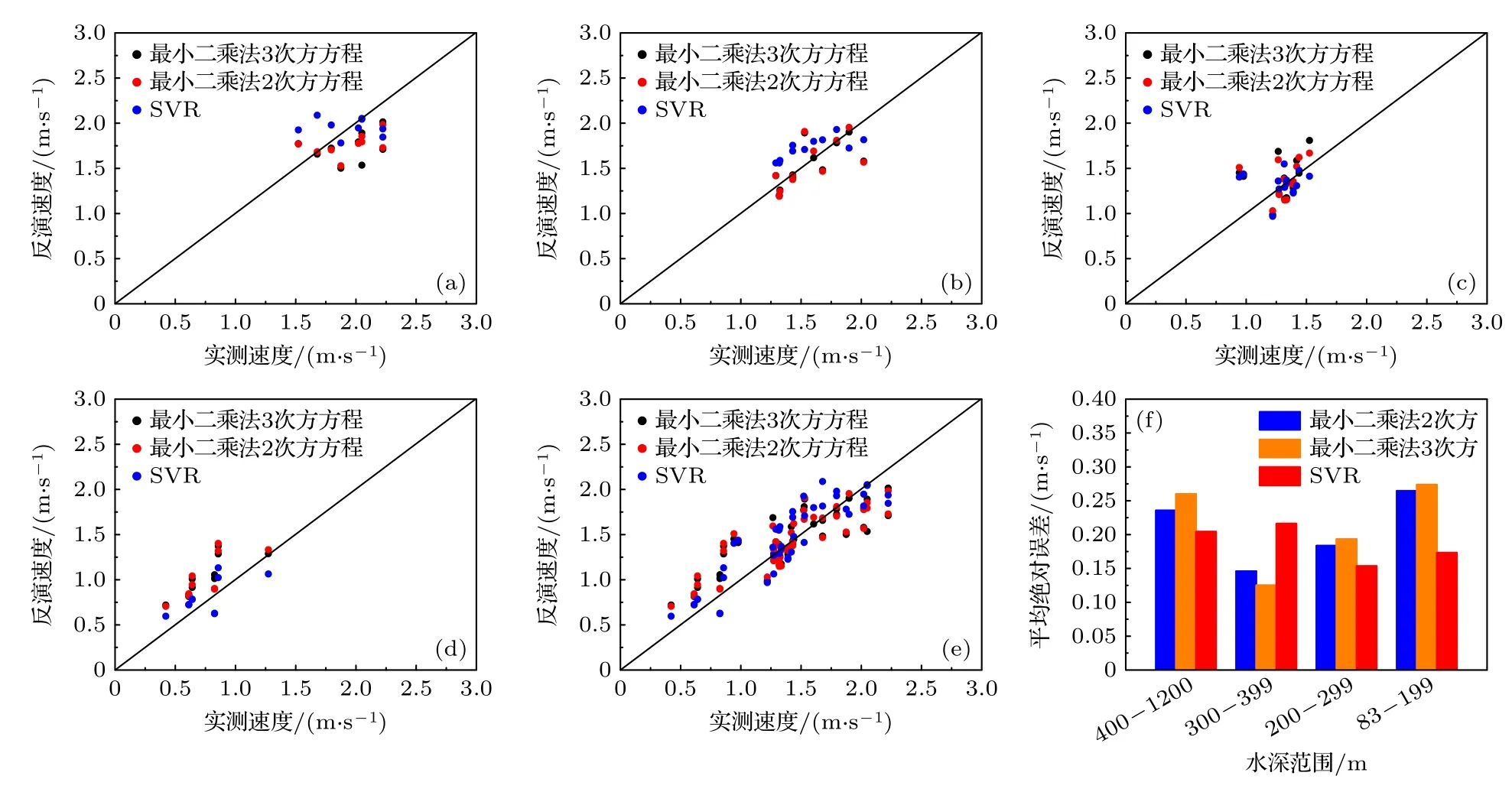
圖7 內孤立波速度反演模型精度驗證圖 (a)—(d) 3 種反演模型對400—1200 m、300—399 m、200—299 m、83—199 m 水深范圍的內孤立波的速度反演結果散點圖;(e) 3 種反演模型對83—1200 m 水深范圍的內孤立波的速度反演結果散點圖;(a)—(e) 黑色散點為最高冪次為2 次方的最小二乘法反演模型結果,紅色散點為最高冪次為3 次方的最小二乘法反演模型結果,藍色散點為SVR 反演模型結果;(f) 三種反演模型對400—1200 m、300—399 m、200—299 m、83—199 m 水深范圍的內孤立波的速度反演結果的平均絕對誤差柱狀圖Fig.7.Precision validation diagram of the internal solitary wave velocity inversion model: (a)–(d) Scatter plots of inversion results of three inversion models for internal solitary waves speed in water depths of 400–1200 m,300–399 m,200–299 m and 83–199 m,respectively;(e) scatter plot of inversion results of three inversion models for internal solitary waves speed in water depths of 83–1200 m;(a)–(e) the black scattered points are the results of least squares inversion model with the highest power of 2,the red scattered points are the results of least squares inversion model with the highest power of 3,and the blue scattered points are the results of SVR inversion model;(f) the average absolute error histogram of the inversion results of the three inversion models for internal solitary waves speed in the water depths of 400–1200 m,300–399 m,200–299 m and 83–199 m.

由圖7(a),(c),(d),(f)可知,SVR 內孤立波速度反演模型在水深400—1200 m 和83—299 m 的范圍精度要高于最小二乘法的兩種模型.由圖7(b),(f)可知在水深范圍300—399 m 時,最小二乘法內孤立波速度反演模型精度較高,其中3 次方的反演模型誤差最小,精度最高.從圖7(f)還可看到,在各個水深二次方和三次方的最小二乘法內孤立波速度反演模型精度相差較小,所以在滿足精度要求時內孤立波速度反演方程就可以采用二次方程描述.

5 總結

本文在實驗室中搭建內孤立波光學遙感仿真平臺,進行了系列仿真實驗.提取并處理實驗數據,建立樣本庫.利用最小二乘法和機器學習SVR 兩種技術建立了內孤立波速度反演模型.共建立了三種反演模型,分別是最小二乘法3 次方內孤立波速度反演模型、最小二乘法2 次方內孤立波速度反演模型和SVR 內孤立波速度反演模型.

收集南海內孤立波光學遙感圖像,提取遙感參數和水文參數,利用多時間圖像法計算內孤立波速度,作為內孤立波現場實測速度,對反演模型精度進行驗證.最小二乘法建立的兩個反演模型對實測數據反演時存在系統誤差,所以利用實測數據對反演模型進行了校正.之后將三種模型按不同水深范圍分別進行精度驗證,結果為: SVR 內孤立波速度反演模型在水深400—1200 m 和水深83—299 m的范圍精度要高于最小二乘法的兩種反演模型,表明了SVR 非線性擬合能力更強.在水深范圍300—399 m 時,最小二乘法內孤立波速度反演模型精度較高,其中3 次方的反演模型誤差最小,精度最高.三種模型的反演精度和誤差基本都在合理范圍,在進行真實海洋條件實際應用時,可以將兩種方法的模型結合應用,當SVR 內孤立波速度反演模型更適用于水深范圍為400—1200 m 或83—299 m,水深范圍在300—399 m 時,優選3 次方最小二乘法內孤立波速度反演模型進行速度反演.兩種方法結合的方式,可以從不同角度理解內孤立波的速度.

通過南海海域遙感數據的驗證可知,最小二乘法內孤立波速度反演模型和SVR 速度反演模型均具有較高精度,最小二乘法內孤立波速度反演模型給出回歸方程進行反演,物理意義更為直觀;SVR 內孤立波速度反演模型則在全水深都具有較高精度.兩種模型都可應用于南海的內孤立波速度反演.