上下游區域間環境保護與生態補償的博弈研究

鄭江麗，楊 川,3，張 康，王 森，黑 亮

(1.水利部珠江河口治理與保護重點實驗室，廣東 廣州 510611； 2.珠江水利科學研究院，廣東 廣州 510611； 3.河海大學水利水電學院，江蘇 南京 210098)

由于不同區域所處的地理位置不同，往往造成區域間自然環境的差異，這種差異使得各區域在經濟發展方面呈現出不同的特點。流域作為一個完整的自然單元，各要素間緊密相連、不可分割，上下游由于自然條件的差別，使得兩者存在較大的經濟差異[1]，如何統籌兼顧上下游經濟發展與環境保護，實現全流域的可持續發展，是擺在上下游面前的一道難題。

流域系統不僅具有整體性，還具有地域分異性，同時面臨著上下游不同利益群體之間的利益沖突，傳統環境經濟學的理論和方法在解決流域問題時遇到了障礙[2]。生態補償是以保護和可持續利用生態系統服務為目的，以經濟手段為主調節相關者利益關系的制度安排[3]。流域上下游的生態補償是在流域形成合理的利益分工條件下，上游地區用水權益讓渡后的利益均衡。因此，相關學者結合博弈理論，為我國流域生態補償制度的順利實施提供研究基礎，實現以生態補償為紐帶促進流域上下游統籌保護和協同發展的目的。馬駿等[4]以微分博弈理論為基礎構建多種生態補償模型，對流域內實施協同生態補償活動以及中央政府制定補貼政策提供了科學依據。劉慧芳等[5]運用完全信息動態博弈、演化博弈理論對東江流域上下游利益相關方的博弈結果與得失進行研究，表明中央財政的支持和監督管理以及政治考評的收益決定了江西和廣東兩省政府對東江治理的意愿和力度。徐大偉等[6]運用演化博弈的方法，分析流域生態補償的特點和結果，表明流域生態補償需要中央政府的適度干預。曲富國等[7]研究認為通過地方政府間有約束力的協議及中央縱向財政轉移支付相結合的模式可實現生態補償的最大效用。劉加伶等[8]基于強互惠主體理論，運用演化博弈方法分析了中央政府、當地政府、地方企業三者之間在長江經濟帶水資源生態開發利用時的利益訴求以及補償行為的動態演化過程。

關于流域生態補償，前人已取得豐富的研究成果，亦表明政府的干預是生態補償政策實施的主要觸發點之一。事實上，生態補償還具有經濟效應和公眾參與效應，針對上述兩方面效應，本文通過系統研究上下游進行環境保護和生態補償時的特征，定義影響博弈雙方行為選擇的具體變量，以此建立上下游的環境保護與生態補償成本收益的博弈模型，并解析相關變量對上下游實施正向措施的影響，以期為流域的生態補償提供參考。

1 博弈演化模型的構建

1.1 模型假設和支付矩陣

上下游是環境保護與生態補償的主體雙方，各個博弈主體都需要承擔相應的責任，博弈雙方是否保護環境、實施生態補償，是在特定的條件下存在的。基于此，本文以博弈論為理論依據，以“誰受益誰補償”為原則[9-10]，構建上下游環境保護與生態補償的演化博弈模型。本文結合上下游區域之間的不完全信息動態博弈過程給出以下4個假設：

假設1：博弈雙方有實施和不實施相應策略的選擇方式。其中，上游區域作為博弈參與者，其策略空間為{保護，不保護}；下游區域的策略空間為{補償，不補償}。

假設2：博弈雙方的決策實施后，能獲得足夠的收益，且不會損害自身的利益。

假設3：上游區域有保護環境和不保護環境的策略。若上游區域實施保護環境的策略，限制相關產業的發展，為下游經濟發達區提供優質的水資源，助力下游的經濟發展；若上游區域為追求經濟發展，選擇不保護環境，使下游區域經濟發展受到約束。

假設4：在生態補償方面，下游區域可以選擇實施或不實施該項策略。若下游區域實施生態補償，是建立在上游區域進行環境保護策略下進行；若上游區域進行環境保護，而下游區域未實施生態補償，則下游區域會因為社會輿論壓力，在經濟方面遭受損失。

上下游區域作為共同面臨環境保護和生態補償策略選擇行為的博弈雙方，定義影響博弈雙方行為選擇的具體變量包括：上游經濟初始收益ES；下游經濟初始收益EX；上游保護環境，延緩經濟發展時的經濟減少系數α；上游保護環境，下游經濟發展的獲益系數β；上游實施保護環境措施且下游實施補償措施時，下游給予上游的經濟補償值B；上游保護環境而下游不實施補償措施時，下游受到輿論壓力，在經濟方面遭受的損失系數ω；當上下游實施正向措施(上游保護環境，下游進行補償)時，由于環境的改善，上下游獲得的環境收益值EH；當上下游實施負向措施(上游不保護環境，下游不進行補償)時，上下游的經濟懲罰系數ε。根據上述假設和變量，構建上下游區域博弈的收益信息如表1所示。

表1 上下游區域間的收益信息

1.2 博弈演化模型的構建

假設上游區域實施環境保護的概率為px(0≤px≤1)，則不實施環境保護的概率為1-px；設下游區域實施生態補償的概率為py(0≤py≤1)，則不實施生態補償的概率為1-py。根據博弈演化理論，設上下游實施正向策略概率px和py的初始值是一定的。由進化博弈模型，可得下列賦值動態方程：

a.對于上游區域，采取環境保護的期望收益S0、不采取環境保護的期望收益S1和上游區域平均期望收益S2分別為

S0=py(ES-αES+B+EH)+(1-py)(ES-αES)

(1)

S1=pyES+(1-py)(ES-εES)

(2)

S2=px[py(ES-αES+B+EH)+(1-py)(ES-
αES)]+(1-px)[pyES+(1-py)(ES-εES)]

(3)

可得上游區域實施環境保護策略的賦值動態方程為

f(px)=px(1-px)[(B+EH-εES)py+ES(ε-α)]

(4)

b.對于下游區域，采取生態補償的期望收益S3、不采取生態補償的期望收益S4和下游區域平均期望收益S5分別為

S3=px(EX+βEX-B+EH)+(1-px)EX

(5)

S4=px(EX+βEX-ωEX)+(1-x)(EX-εEX)

(6)

S5=py[px(EX+βEX-B+EH)+(1-px)EX]+
(1-py)[px(EX+βEX-ωEX)+
(1-px)(EX-εEX)]

(7)

則下游區域實施生態補償策略的賦值動態方程為

f(py)=py(1-py){[EX(ω-ε)-B+EH]px+εEX}

(8)

將上下游的復制動態方程聯立構成方程組，得到上下游區域在生態補償策略方面的博弈演化模型：

(9)

分別對f(px)和f(py)求偏導，得到博弈演化模型的雅可比矩陣：

(10)

根據雅克比矩陣得到矩陣的行列式detJ和矩陣的跡trJ分別為

detJ=(1-2px)[(B+EH-εES)py+ES(ε-α)]·
(1-2py){[EX(ω-ε)-B+EH]px+εEX}-px(1-px)·
(B+EH-εES)py(1-py)[EX(ω-ε)-B+EH]

(11)

tr(J)=(1-2px)[(B+EH-εES)py+ES(ε-α)]+
(1-2py){[EX(ω-ε)-B+EH]px+εEX}

(12)

1.3 演化穩定策略分析

博弈系統在平面內的5個局部均衡點分別為(0，0)、(0，1)、(1，0)、(1，1)和(x*,y*)。由上述5個均衡點得到矩陣行列式detJ和跡trJ的表達式，如表2所示。

表2 均衡點對應的矩陣行列式和跡的表達式

根據Friedman[11]提出的方法，行列式detJ>0和矩陣的跡trJ<0時，則該局部平衡點即為上游區域和下游區域實施相應策略的進化穩定策略[11]。對于(x*,y*)，trJ恒等于0，不符合trJ<0的條件，因此不予討論。依次分析各個局部均衡點對應的雅克比矩陣的行列式及其跡，以此得出各個局部平衡點的穩定性：①若均衡點(0,0)為演化穩定策略，需要滿足條件ε<α，且εEX<0；由于εEX一定大于零，因此均衡點(0,0)不可能成為演化穩定策略，即上游區域和下游區域不會同時實行否定策略，即上游不進行環境保護，下游不實施生態補償策略。②若αES-B-EH>0，則均衡點(0,1)為演化穩定策略。③若α<ε且B-EH-ωEX>0，則均衡點(1,0)為演化穩定策略。④若αES-B-EH<0且ωEX-B+EH>0，則均衡點(1,1)為演化穩定策略。

2 博弈模型仿真分析

前述分析結果顯示，當αES-B-EH>0時，上游實施的策略為環境保護策略，導致延緩經濟發展，由于經濟受損較大且獲得的補償較小，此時上游將不實施環境保護策略，均衡演化點為(0，1)；當α<ε且B-EH-ωEX>0時，；因上游保護環境，下游需要給與的補償較大，因此下游區域將不實施生態補償措施，此時的均衡演化點為(1，0)。由于上下游區域均實施正向策略為最優策略，本文將重點解析均衡點(1,1)為演化穩定策略時的情形。

分析前述8項參數在滿足αES-B-EH<0和B-EH-ωEX<0的條件時進行演化的過程。為了更好地分析上下游之間的策略選擇變化，本文通過對各參數賦值的方式進行模擬仿真。

a.各參數取值為：ES=150，EX=300，α=0.3，β=0.2，B=100，ω=0.3，ε=0.4，EH=50，對該假定數值進行模擬，分析上游區域實施保護策略的比例x與下游區域實施補償策略的比例y之間的相互關系，以及兩者隨時間的變化情況，結果見圖1。

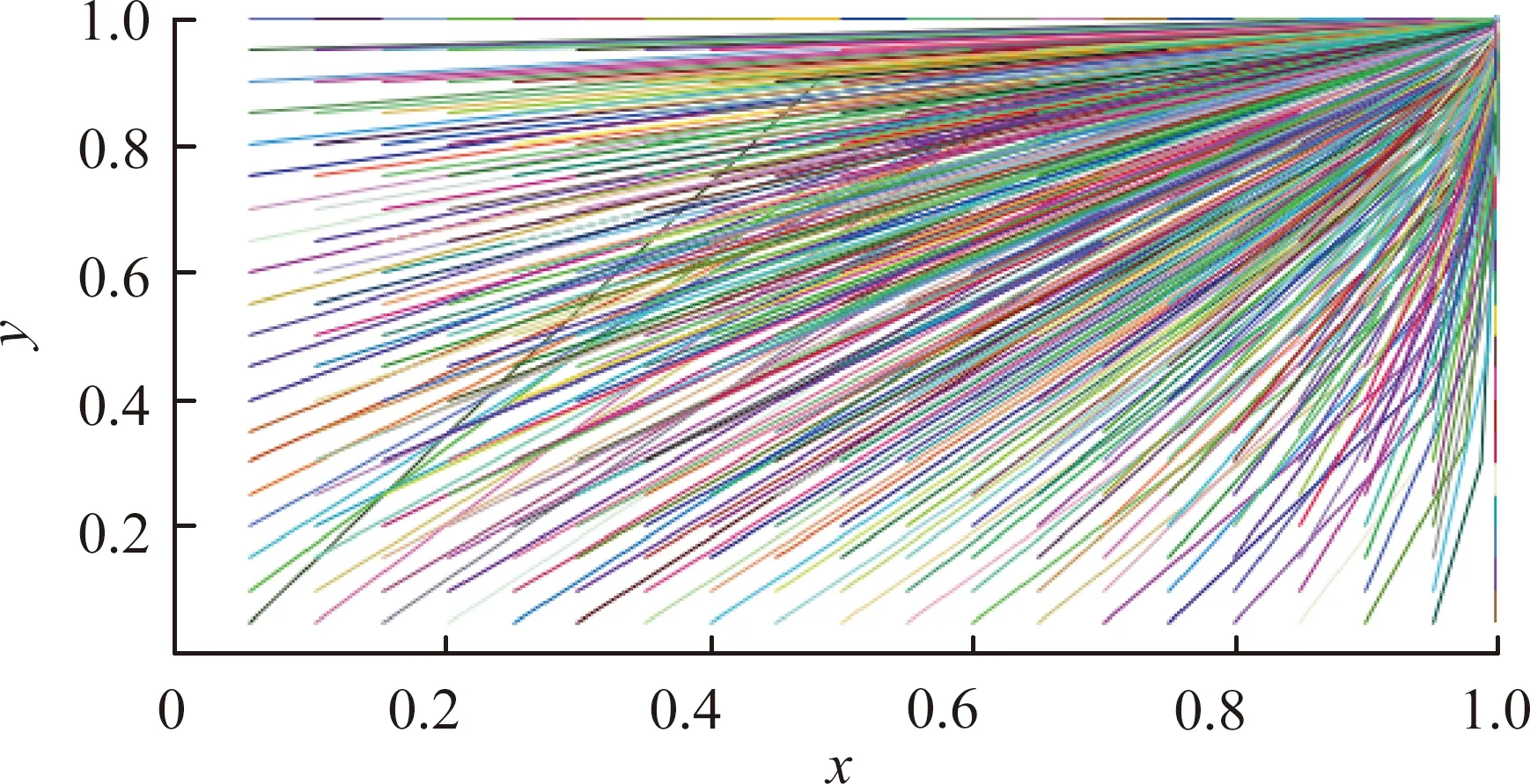
(a) 博弈雙方演化策略

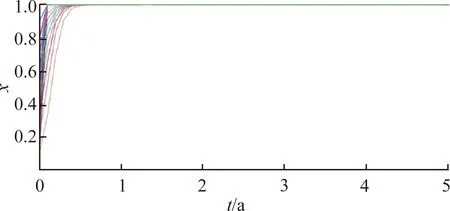
(b) 上游區域不同時間的演化策略

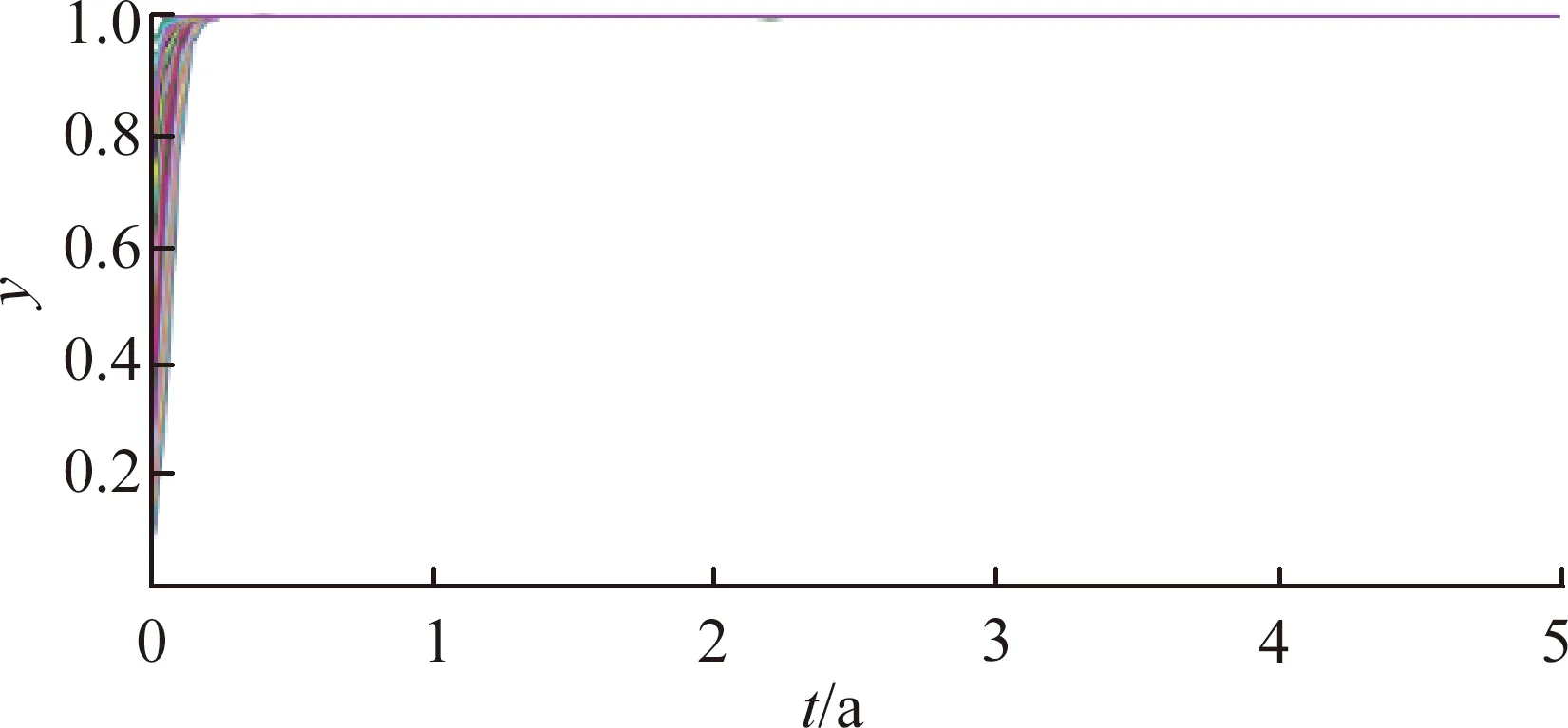
(c) 下游區域不同時間的演化策略圖1 均衡演化點為(1，1)的模擬演算結果

圖1表明，當輸入的數據滿足αES-B-EH<0且B-EH-ωEX<0時，上下游區域在該條件下進行博弈，最終的博弈結果為：上游區域實施環境保護策略，下游區域對上游區域進行生態補償。

進一步解析相關變量對上下游實施正向措施的影響。根據均衡演化點為(1，1)的條件，影響均衡演化點(1，1)的博弈演化過程的參數有ES、B、EH、EX、ω和α，本文進一步分析ES、EH、B和EX對均衡演化點(1，1)的影響。

b.當上游經濟初始收益減少時，即ES由150調整為50，其他參數不變(EX=300，α=0.3，β=0.2，B=100，ω=0.3，ε=0.4，EH=50)時，對該假定數值進行模擬，雙方的博弈過程如圖2所示。

(a) 博弈雙方演化策略

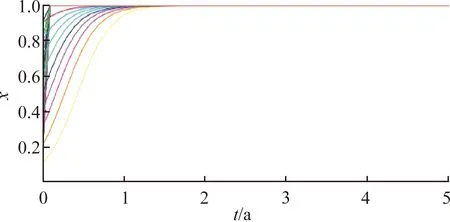
(b) 上游區域不同時間的演化策略

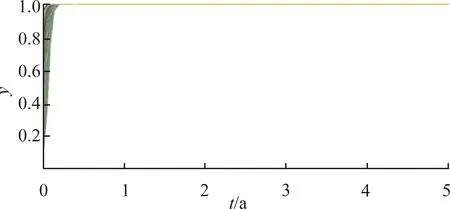
(c) 下游區域不同時間的演化策略圖2 上游區域初始經濟狀況較低時的模擬演算結果

圖2表明，上游區域經濟狀況的初始水平對上游區域是否實施環境保護策略具有一定的影響。圖2(b)中上游區域實施補償策略時收斂到x=1的時間較長，即上游經濟初始狀況較差時進行環境保護意愿與上游經濟初始狀況較好時進行環境保護的意愿相比呈現減小的趨勢，原因是相對于上游區域初始經濟條件較好的情形，上游區域初始經濟收益較低時對環境的影響、污染情況更小，進行環境保護的效果難以體現，使得初始經濟條件偏差的上游區域進行環境保護的意愿度弱于初始經濟條件較好的上游區域。圖2(c)顯示，上游區域的初始經濟狀況的改變，對于下游區域實施補償措施的影響不大。

在圖2演化結果基礎上，將環境收益值EH由初始的50增大到200，其他參數分別為：ES=50，EX=300，α=0.3，β=0.2，B=100，ω=0.3，ε=0.4，對該假定數值進行模擬，所得的上下游間博弈結果和圖2相比差異不大，即環境收益的改變對上下游實施正向措施的影響不大，本文未將結果列出。

c.進一步分析下游區域補償上游區域對上下游實施正向措施的影響，此時的假定數值為：B=270，ES=50，EX=300，α=0.3，β=0.2，ω=0.3，ε=0.4，EH=200，分析經濟補償對上下游區域采取正向措施意愿度的影響，結果如圖3所示。

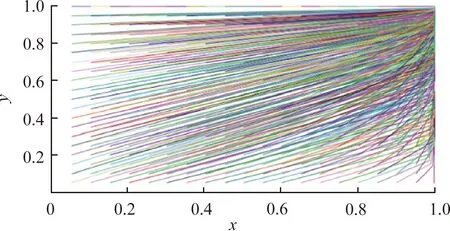
(a) 博弈雙方演化策略

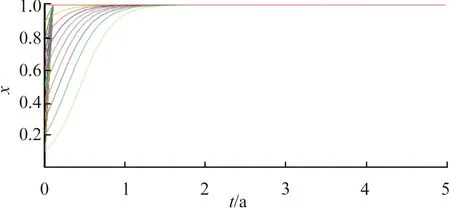
(b) 上游區域不同時間的演化策略

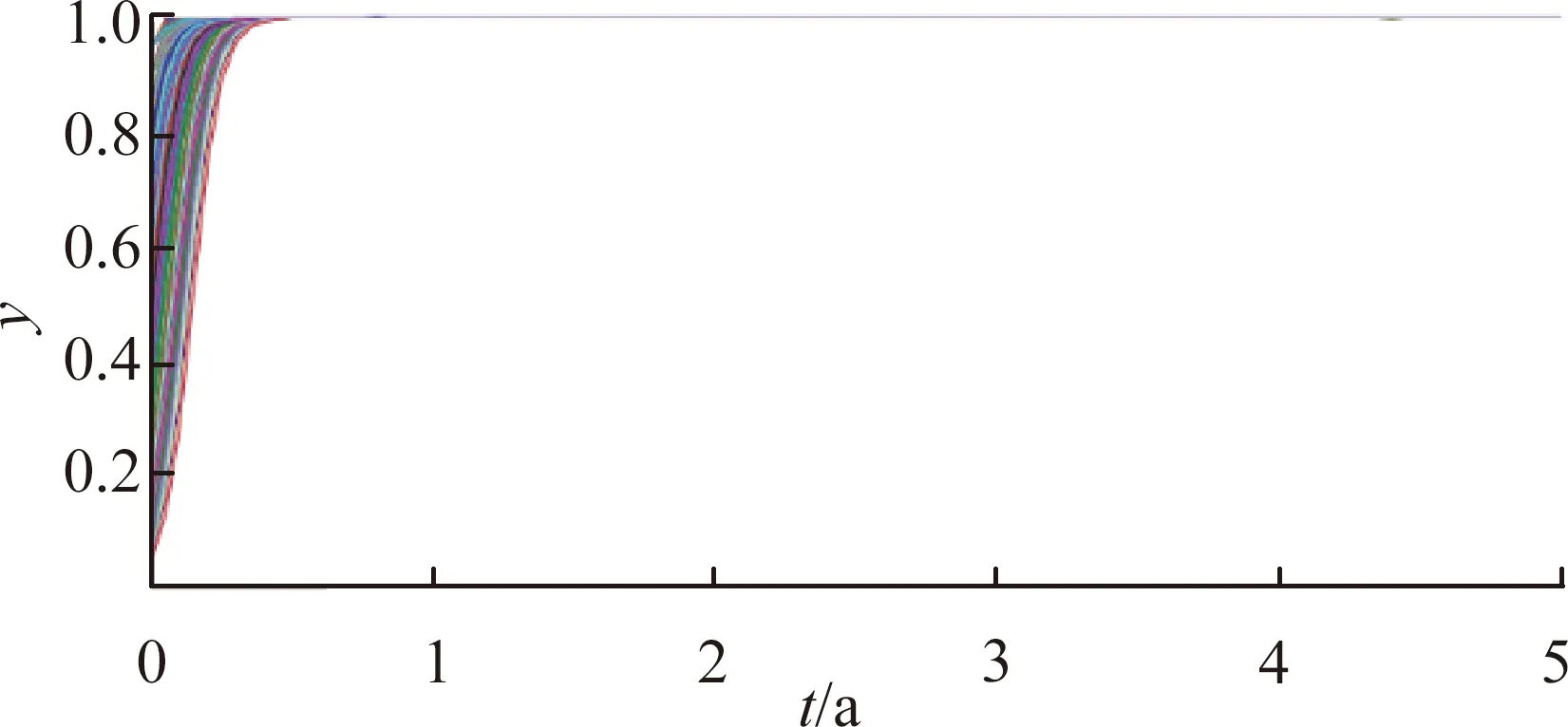
(c) 下游區域不同時間的演化策略圖3 下游區域對上游區域補償值改變時的模擬演算結果

圖3表明，整體而言，補償值的改變對上游采取環境保護措施的意愿度影響不大；對下游采取生態補償的正向措施有一定的影響。具體表現為：圖3(c)中下游區域實施補償策略時收斂到y=1的時間較長。由于假定的數值仍舊滿足條件αES-B-EH<0且B-EH-ωEX<0，因此上下游依舊實施正向措施，即上游采取環境保護措施，下游進行生態補償。

d.進一步分析下游經濟初始收益對上下游實施正向措施的影響。將相關參數的數值設置為：EX=500，ES=50，α=0.3，β=0.2，B=270，ω=0.3，ε=0.4，EH=200，分析此時的上下游博弈演化過程，結果如圖4所示。

(a) 博弈雙方演化策略

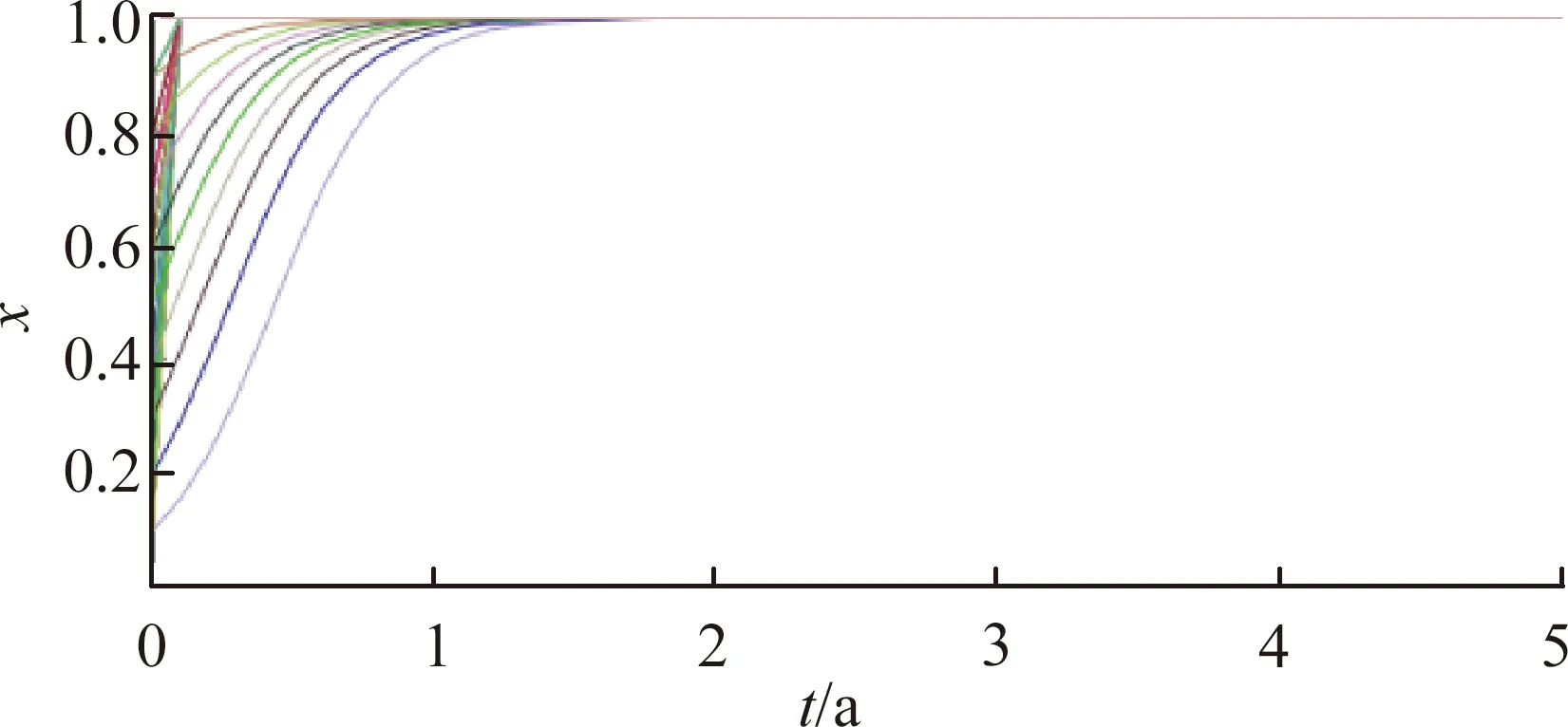
(b) 上游區域不同時間的演化策略

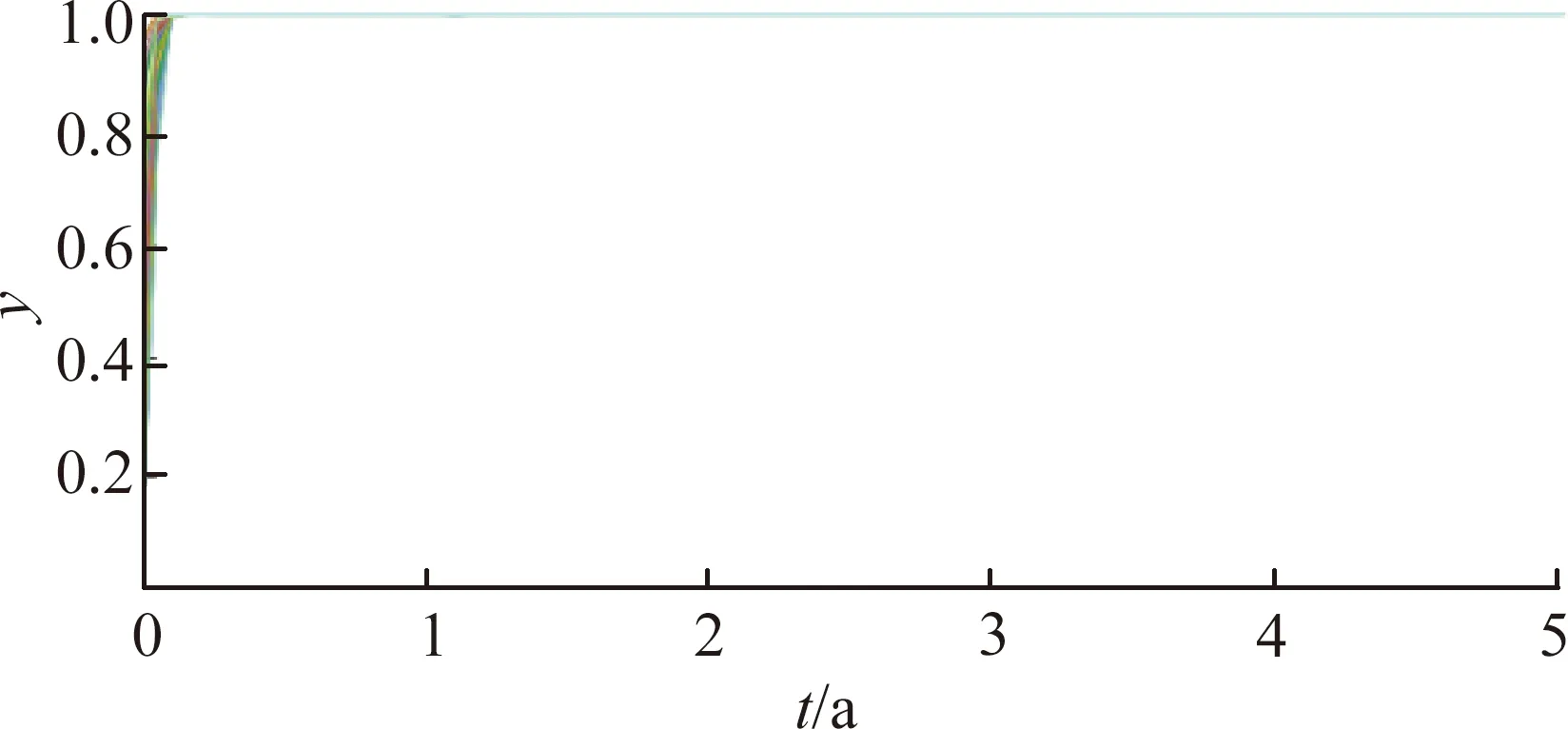
(c) 下游區域不同時間的演化策略圖4 改變下游區域的經濟初始收益時的模擬演算結果

由于在圖1～3的上下游博弈演化過程中，EX均為300，此時下游初始經濟條件好，上下游的博弈過程顯示如下：上游采取環境保護措施意愿幾乎沒有影響，而對下游采取生態補償的意愿度有顯著影響，表現為圖4(c)中下游區域實施補償策略時收斂到y=1的時間急劇縮短，說明下游經濟條件越好，越希望獲取優質的水源資源，因此下游區域采取補償措施的意愿度迅速增加。

3 結 論

a.若上游區域實施的環境保護策略導致延緩經濟發展，由此帶來上游區域經濟減少量大于獲得的生態補償，此時上游將不實施環境保護策略；若下游需要給予的補償值較大，綜合效益不高，下游區域將不實施生態補償的措施；上游區域實施環境保護策略且下游區域采取生態補償措施，需要建立在一定的條件基礎上。

b.環境收益值的變化對上下游采取正向措施意愿度的影響較小；上游經濟初始狀況越差，上游區域傾向于進行環境保護的意愿度越低；下游對上游的補償越大，下游區域采取補償措施的意愿度越低；下游區域初始經濟狀況越好，下游區域采取補償措施的意愿度越高。

c.在制定上下游生態保護策略和生態補償機制時，應當充分考慮當地初始經濟狀況，制定適當的政策和制度，積極調動上游生態保護積極性，保證上游經濟收入不低于保護前的利益獲得；對于下游需要付出的生態補償，應兼顧自身環境保護和經濟發展，使得下游經濟在一定條件限制下充分發展，對上游進行生態補償。由此統籌協調環境保護和經濟發展，使得環境和經濟綜合效益最大化。對上下游利益相關體進行生態補償博弈研究時，必須考慮各利益體的自身發展狀況，當生態補償或環境保護損失的利益超過利益體承受邊界時，往往無法取得理想的協調效果。