把握兩個關鍵點,求解離散型隨機變量的分布列

李桂春

(北京師范大學附屬實驗中學)

新高考關注培養學生閱讀和審題的習慣,關注生活與數學的聯系,注重培養學生在復雜情境下解決數學問題的能力.概率與統計的試題正是以生活實際問題為背景,考查學生閱讀理解、推理分析、數據運算等能力,因此每年的高考試題中均有涉及.而在概率統計的試題中經常考查離散型隨機變量的分布列.對于離散型隨機變量的分布列,首先要把握概念的本質,理解概念中的關鍵要素,才能合理地運用概率模型計算離散型隨機變量各個取值對應的概率,從而得到離散型隨機變量的分布列.

求解離散型隨機變量的分布列時,把握以下兩個關鍵點:

1)正確寫出離散型隨機變量X的所有可能取值xk(k＝1,2,3,…,n);

2)求出離散型隨機變量取每一個值的概率P(X＝xk)＝pk(k＝1,2,…,n),在求概率時要分清用哪一種概率模型來解決.

1 正確寫出離散型隨機變量的所有可能取值

求解離散型隨機變量的分布列的關鍵點之一是明確隨機變量的所有可能取值,以及取每一個值時對應的意義,有時一個隨機變量的取值可能對應一個或多個隨機試驗的結果,在解答過程中不要漏掉某些試驗結果.

例1從裝有6個白球、4個黑球和2個黃球的箱中隨機地取出兩個球,規定每取出一個黑球得2分,而每取出一個白球失1分,取出黃球不得分,以X表示所得的分數,隨機變量X可以取哪些值呢? 求X的分布列.

當取到2個白球時,X＝－2;

當取到1個白球和1個黃球時,失1分,X＝－1;

當取到1個白球和1個黑球時,X＝1;

當取到2個黃球時,X＝0;

當取到1個黑球和1個黃球時,X＝2;

當取到2個黑球時,X＝4.

X的所有可能取值為－2,－1,0,1,2,4,則

所以X的分布列如表1所示.

表1

例2盒子中裝著標有數字1,2,3,4,5 的卡片各2張,從盒子中任取3張卡片,每張卡片被取出的可能性都相等,用ξ表示取出的3張卡片上的最大數字,求:

(1)取出的3張卡片上的數字互不相同的概率;

(2)隨機變量ξ的概率分布.

(2)由題意知ξ的所有可能取值為2,3,4,5,則

所以隨機變量ξ的分布列如表2所示.

表2

2 分析離散型隨機變量分布列的模型,合理選擇計算概率的方法

2.1 超幾何分布,利用古典概型計算概率

(1)求某位消費者在一次抽獎活動中抽到的4張卡片上都印有“幸”字的概率;

(2)記隨機變量X為某位消費者在一次抽獎活動中獲得代金券的金額數,求X的分布列和數學期望E(X);

(3)該商家規定,消費者若想再次參加該項抽獎活動,則每抽獎一次需支付3元.若你是消費者,是否愿意再次參加該項抽獎活動? 請說明理由.

(2)隨機變量X的所有可能取值為10,5,0,則

所以X的分布列如表3所示.

表3

(3)方法1記隨機變量Y為消費者在一次抽獎活動中的收益,則.因此不愿意再次參加該項抽獎活動.

方法2記“某位消費者在一次抽獎中能獲得獎券”為事件B,則因為中獎概率不足因此不愿意再次參加該項抽獎活動.

板安窯村為了幫助貧困戶，提供了打掃衛生的公益崗位，一個月500塊錢，但是很多人看不到眼里，覺得錢少。知道消息的郭書鳳馬上找到了村干部，并爽快地接住了這個工作。

例4已知某單位甲、乙、丙三個部門的員工人數分別為24,16,16.現采用分層抽樣的方法從中抽取7人,進行睡眠時間的調查.

(1)應從甲、乙、丙三個部門的員工中分別抽取多少人?

(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,現從這7人中隨機抽取3人做進一步的身體檢查.

(ⅰ)用X表示抽取的3人中睡眠不足的員工人數,求隨機變量X的分布列與數學期望;

(ⅱ)設A為事件“抽取的3人中,既有睡眠充足的員工,也有睡眠不足的員工”,求事件A發生的概率.

(2)(ⅰ)隨機變量X的所有可能取值為0,1,2,3,則,所以隨機變量X的分布列如表4所示.

表4

(ⅱ)設事件B為“抽取的3人中,睡眠充足的員工有1人,睡眠不足的員工有2人”;事件C為“抽取的3人中,睡眠充足的員工有2人,睡眠不足的員工有1人”,則A＝B∪C,且B與C互斥,由(ⅰ)知,P(B)＝P(X＝2),P(C)＝P(X＝1),故P(A)＝P(B∪C)＝P(X＝2)＋P(X＝1)＝所以事件A發生的概率為

啟示解決上面兩道有關離散型隨機變量分布列問題的關鍵是分清隨機變量的分布列是超幾何分布,用古典概型計算其概率.超幾何分布描述的是不放回抽樣問題,隨機變量為抽到的某類個體的個數.超幾何分布的特征:1)考查對象分兩類;2)已知各類對象的個數;3)從中抽取若干個個體,考查某類個體個數X的概率分布.

2.2 二項分布,利用獨立重復試驗計算概率

例5共享交通工具的出現極大地方便了人們的生活,也是當下一個很好的發展商機.某公司根據市場發展情況推出共享單車和共享電動車兩種產品.市場調查發現,兩種產品中,共享電動車速度更快,更受消費者歡迎,一般使用共享電動車的概率為,使用共享單車的概率為.該公司為了促進大家消費,使用共享電動車一次記2分,使用共享單車一次記1分.每個市民各次使用共享交通工具選擇意愿相互獨立,市民之間選擇意愿也相互獨立.

(1)現有4 位市民使用該公司共享交通工具出行,求至少有一人使用共享單車的概率;

(2)從首次使用共享交通工具的市民中隨機抽取3人,記總得分為隨機變量ξ,求ξ的分布列.

設“至少有一人使用共享單車”為事件A,則

(2)由題意,從首次使用共享交通工具的市民中隨機抽取3人,總得分ξ的可能取值為3,4,5,6,則

所以ξ的分布列如表5所示.

表5

例6為了防止受到核污染的產品影響我國民眾的身體健康,要求產品在進入市場前必須進行兩輪核輻射檢測,只有兩輪都合格才能進行銷售,否則不能銷售.已知某產品第一輪檢測不合格的概率為,第二輪檢測不合格的概率為,兩輪檢測是否合格相互沒有影響.

(1)求該產品不能銷售的概率;

(2)如果產品可以銷售,則每件產品可獲利40元;如果產品不能銷售,則每件產品虧損80元(即獲利－80元).已知一箱中有產品4件,記一箱產品獲利X元,求X的分布列,并求出均值E(X).

P(A)＝1－,所以該產品不能銷售的概率為

(2)由已知,4件產品能否銷售有以下5種情形:

4件不能銷售,0件能銷售,對應的X取值為－320;

3件不能銷售,1件能銷售,對應的X取值為－200;

2件不能銷售,2件能銷售,對應的X取值為－80;

1件不能銷售,3件能銷售,對應的X取值為40;

0件不能銷售,4件能銷售,對應的X取值為160.

X的所有可能取值為－320,－200,－80,40,160,則

所以X的分布列如表6所示.

表6

2.3 利用相互獨立事件的概率公式計算

例7從甲地到乙地要經過3個十字路口,設各路口信號燈工作相互獨立,且在各路口遇到紅燈的概率分別為

(1)設X表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量X的分布列和數學期望;

(2)若有2輛車獨立地從甲地到乙地,求這2輛車共遇到1個紅燈的概率.

所以隨機變量X的分布列如表7所示.

表7

(2)設有2輛車獨立地從甲地到乙地,這2輛車共遇到1個紅燈為事件A,則

2.4 辨別離散型隨機變量滿足的分布列,采用相應的計算概率的方法

例8袋中有8個白球、2個黑球,從中隨機地連續抽取3次,每次取1個球.

(1)若每次抽取后都放回,設取到黑球的個數為X,求X的分布列;

(2)若每次抽取后都不放回,設取到黑球的個數為Y,求Y的分布列.

所以X的分布列如表8所示.

表8

(2)若每次抽取后都不放回,則隨機抽取3次可看成隨機抽取1次,但1次抽取了3個球,因此黑球數Y服從參數為10,3,2 的超幾何分布,即Y～H(10,3,2),因此

所以Y的分布列如表9所示.

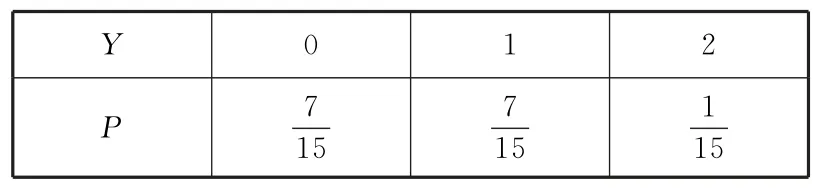
表9

啟示在產品檢驗中,若N件產品中,共有M件次品,當我們從這些產品中每次抽取一件,共抽取n次進行檢查時,若是有放回地抽樣,則抽到的次品數X服從的是二項分布;若是不放回地抽樣且n≤N,則抽到的次品數X服從的是超幾何分布.

例9某校高二(1)班的一個研究性學習小組在網上查知,某植物種子在一定條件下發芽成功的概率為,該研究性學習小組又分成兩個小組進行驗證性試驗.

(1)第一小組做了5次這種植物種子的發芽試驗(每次均種下一粒種子),求他們的試驗中至少有3次發芽成功的概率;

(2)第二小組做了若干次發芽試驗(每次均種下一粒種子),如果在一次試驗中種子發芽成功就停止試驗,否則將繼續進行下次試驗,直到種子發芽成功為止,但試驗的次數最多不超過5次.求第二小組所做種子發芽試驗的次數ξ的概率分布列.

所以至少有3次發芽成功的概率為

(2)隨機變量ξ的所有可能取值為1,2,3,4,5,則

所以ξ的分布列如表10所示.

表10

啟示本題中的第(1)問中至少有3 次發芽成功,即有3次、4次、5次發芽成功.而其中每一種情況,例如,有4次發芽成功,只需在5次中恰有4次成功即可,故滿足獨立重復試驗;第(2)問中的隨機變量取每一個值,例如,ξ＝4時,是前3次未發芽,第4次才發芽,故不滿足獨立重復試驗,應按相互獨立事件的概率計算.

例102016年微信用戶數量統計顯示,微信注冊用戶數量已經突破9.27億.微信用戶平均年齡只有26歲,97.7%的用戶在50 歲以下,86.2%的用戶在18～36歲之間.為調查大學生這個微信用戶群體中每人擁有微信群的數量,現從北京市大學生中隨機抽取100位同學進行了抽樣調查,結果如表11所示.

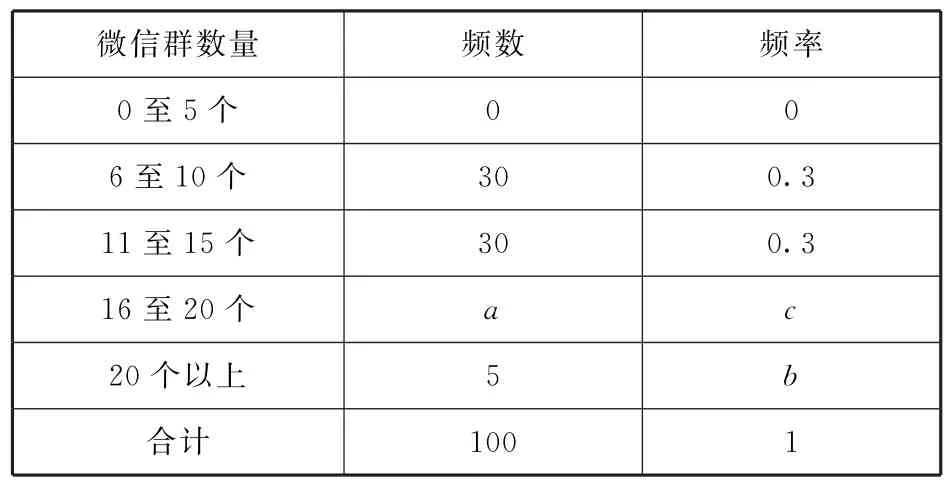
表11

(1)求a,b,c的值;

(2)若從這100 位同學中隨機抽取2 人,求這2人中恰有1人微信群個數超過15個的概率;

(3)以這100個人的樣本數據估計北京市的總體數據且以頻率估計概率,若從全市大學生中隨機抽取3人,記X表示抽到的是微信群個數超過15個的人數,求X的分布列和數學期望E(X).

(2)記“2人中恰有1人微信群個數超過15個”為事件A,則所以2 人中恰有1人微信群個數超過15個的概率為

所以X的分布列如表12所示.

表12

啟示此題要分清超幾何分布和二項分布的區別,超幾何分布中隨機變量取某一值時的概率符合古典概型,古典概型需滿足有限性,即在一次試驗中,基本事件發生的次數是有限的.第(2)問是在樣本中考慮,從100人中隨機抽取2人,符合古典概型.當隨機變量的總體很大且抽取的樣本容量相對于總體來說又比較小,且每次抽取時又只有兩種試驗結果,此時可以把它看成獨立重復試驗,利用二項分布求其分布列.第(3)問是利用樣本估計總體,在北京市的總體數據中抽取,符合二項分布.

在求離散型隨機變量的分布列時,一般按照如下步驟進行:分析題意→分別寫出取值所表示的結果→寫出X的所有可能取值→求出X取每一個值的概率→列表得出X的分布列.

在具體過程中,應把握兩個關鍵點:

1)離散型隨機變量的所有可能取值及對應的隨機試驗結果,二者之間可以相互轉化;

(2)分清分布列的模型,并用相應的概率公式計算,這樣就能準確高效地解答有關離散型隨機變量的分布列問題.

(完)