面向綠色智能制造的高維多目標(biāo)動態(tài)作業(yè)車間調(diào)度優(yōu)化
李 稚, 周雙牛
(天津工業(yè)大學(xué) 經(jīng)濟與管理學(xué)院,天津 300387)
0 引言
國務(wù)院于2015年部署“中國制造2025”戰(zhàn)略,提出把綠色發(fā)展作為主攻方向之一,構(gòu)建高效、低碳、循環(huán)的綠色制造體系,以自動化技術(shù)、信息技術(shù)為核心的先進制造技術(shù)推動我國制造業(yè)向智能化和綠色化方向發(fā)展。十九大報告提出“生態(tài)優(yōu)先、綠色發(fā)展”的制造業(yè)發(fā)展理念,指導(dǎo)制造企業(yè)綠色轉(zhuǎn)型升級,以實現(xiàn)可持續(xù)發(fā)展戰(zhàn)略目標(biāo)。基于此,綠色發(fā)展理念在人工智能和大數(shù)據(jù)背景下,工業(yè)化與信息化的融合,催生了新的工業(yè)發(fā)展形態(tài)——綠色智能制造,即基于新一代信息技術(shù)與制造技術(shù)深度融合,將環(huán)保理念應(yīng)用于生產(chǎn)制造活動中,實現(xiàn)節(jié)能減排的新型制造模式[1,2]。綠色智能制造深刻改變了傳統(tǒng)制造企業(yè)的生產(chǎn)模式,如何面對智能化生產(chǎn)轉(zhuǎn)型和升級,綠色智能車間的建立及運營是關(guān)鍵。柔性作業(yè)車間調(diào)度是綠色智能制造的核心問題,需要綜合考慮環(huán)境、指標(biāo)等多個相沖突目標(biāo),在資源約束條件下提出一系列綠色低碳的作業(yè)車間調(diào)度方案。高效智能的調(diào)度策略能夠優(yōu)化企業(yè)的生產(chǎn)運作管理,助力我國綠色智能制造業(yè)的穩(wěn)健發(fā)展。
近年來,有學(xué)者初涉綠色作業(yè)車間調(diào)度領(lǐng)域研究。李益兵等[3]提出從碳排放量、噪聲及廢棄物三個方面綜合評定環(huán)境污染等級,建立以極小化最大完工時間和環(huán)境污染程度為目標(biāo)的多目標(biāo)綠色柔性作業(yè)車間調(diào)度模型;劉彩潔等[4]考慮分時電價政策,建立以極小化最大完工時間、碳排放和能耗成本的綠色柔性作業(yè)車間調(diào)度多目標(biāo)優(yōu)化模型,實現(xiàn)了時間、經(jīng)濟和能耗三者的協(xié)同優(yōu)化;李聰波等[5]對機床加工過程中消耗的直接能源和間接能源進行研究,提出廣義能耗概念,建立能耗多目標(biāo)優(yōu)化模型,并開發(fā)模擬退火算法對柔性作業(yè)車間調(diào)度模型求解。以上研究主要對環(huán)境污染或能源消耗方面進行分析,在研究目標(biāo)中加入綠色指標(biāo),但約束條件尚未考慮綠色約束。研究得到的優(yōu)化解,大多是在傳統(tǒng)車間調(diào)度問題結(jié)果中選出綠色指標(biāo)較優(yōu)的方案。然而,在實際綠色柔性作業(yè)車間調(diào)度過程中需要全方面考慮綠色因素,即在目標(biāo)函數(shù)和約束條件中均涉及綠色指標(biāo)。顯然,現(xiàn)有研究在綠色柔性作業(yè)車間調(diào)度模型構(gòu)建方面具有一定局限性。
多目標(biāo)柔性作業(yè)車間調(diào)度問題,現(xiàn)有研究主要基于Pareto尋優(yōu)的方法[6]直接在多目標(biāo)空間中尋優(yōu),其中非支配排序遺傳算法[7]和多目標(biāo)粒子群算法[8]是比較成熟和理想的Pareto尋優(yōu)算法。Komaki等[9]首次將灰狼優(yōu)化(Grey Wolf Optimizer, GWO)算法應(yīng)用于生產(chǎn)調(diào)度問題,實驗表明GWO算法優(yōu)于其他元啟發(fā)式算法,然而該研究是對GWO算法的簡單應(yīng)用,并未解決復(fù)雜生產(chǎn)調(diào)度問題;Tawhid等[10]運用差分進化對GWO算法中包圍獵物操作進行改進,但改進后的算法只適合用于連續(xù)型問題的求解。柔性作業(yè)車間調(diào)度問題具有復(fù)雜性,目前研究目標(biāo)主要集中于最大完工時間、成本、機器負(fù)荷等生產(chǎn)指標(biāo),由于求解算法的局限性,現(xiàn)有研究大多同時考慮2~3個目標(biāo),關(guān)注目標(biāo)較少。高維多目標(biāo)柔性作業(yè)車間調(diào)度是實際生產(chǎn)作業(yè)的真實反映。目前,鮮有研究將總能耗等綠色指標(biāo)納入多目標(biāo)模型構(gòu)建中,并同時考慮4個及以上目標(biāo)的高維多目標(biāo)[11]柔性作業(yè)車間調(diào)度問題。
綜上,現(xiàn)有文獻大多關(guān)注最大完工時間的優(yōu)化問題,而忽略實際生產(chǎn)中其他重要因素,如污染排放、機器負(fù)荷、產(chǎn)品質(zhì)量等。也有學(xué)者只針對綠色作業(yè)車間調(diào)度或者動態(tài)調(diào)度問題進行單一維度研究,尚未發(fā)現(xiàn)將二者結(jié)合進行多維度柔性車間調(diào)度研究。基于此,本文開發(fā)高效智能優(yōu)化算法——改進的多目標(biāo)灰狼優(yōu)化算法(Improved Multi-objective Grey Wolf Optimizer, IMOGWO)對高維多目標(biāo)綠色動態(tài)柔性作業(yè)車間調(diào)度問題(Many Objective Green Dynamic Flexible Job-shop Scheduling Problem, MaO-GDFJSP)進行求解,提出最優(yōu)的作業(yè)車間調(diào)度方案。本研究主要創(chuàng)新點為:(1)考慮不同機器狀態(tài)下的能耗情況,以及機器使用節(jié)能方法,建立了基于機器故障,研究總能耗、最大完工時間、機器總負(fù)荷和產(chǎn)品質(zhì)量穩(wěn)定性的高維4目標(biāo)的MaO-GDFJSP模型;(2)創(chuàng)造性地提出多級官員領(lǐng)導(dǎo)機制,將灰狼種群改為多層多級結(jié)構(gòu),有利于擴大種群多樣性;(3)將遺傳算法中優(yōu)秀因子引入灰狼算法,如POX交叉算子、逆轉(zhuǎn)算子,尤其是依據(jù)Pareto解集提出自適應(yīng)精英保留策略,提高了種群更新效率和質(zhì)量。
1 MaO-GDFJSP模型的建立
1.1 MaO-GDFJSP的描述
MaO-GDFJSP是綠色制造的重要問題。MaO-GDFJSP問題描述:車間有n個工件需要在m臺機器上進行加工,其中每個工件有ni道工序,每道工序的可選加工機器集Mij及其加工時間已知。MaO-GDFJSP問題基于綠色調(diào)度和動態(tài)調(diào)度,對生產(chǎn)加工中的多個目標(biāo)進行綜合決策以尋找滿足復(fù)雜條件的調(diào)度方案。選取生產(chǎn)加工中常用的極小化總能耗、最大完工時間、機器總負(fù)荷和產(chǎn)品質(zhì)量穩(wěn)定性4個目標(biāo)。此外,還需考慮以下假設(shè)條件:
(1)在初始時刻所有工件處于待加工狀態(tài),所有機器處于空閑狀態(tài);
(2)同一時刻,每臺機器只能加工一個工件,每個工件只能被一臺機器所加工;
(3)工件加工過程中不能中斷;
(4)同一工件不同工序之間有先后順序,不同工件之間無先后順序;
(5)忽略機器啟動及換型時間、工件運輸時間及重調(diào)度計算時間[12]。
1.2 數(shù)學(xué)模型的建立
為描述問題方便,定義符號及其含義如下(見表1)。

表1 主要符號及其說明
在前人對動態(tài)車間調(diào)度和多目標(biāo)車間調(diào)度問題基礎(chǔ)上,建立適合MaO-GDFJSP的混合整數(shù)規(guī)劃模型,表示為min(E,T,L,Q)。
(1)總能耗E是綠色智能制造下需要考慮的重要指標(biāo)。在實際生產(chǎn)中,總能耗可分為加工能耗和空載能耗,加工能耗是指機器加工工件時所消耗的能量,如式(2)所示;空載能耗是指在下一工件到達(dá)之前機器空轉(zhuǎn)所消耗的能量,如式(3)所示。
(1)
(2)
Eq=[max(Xijh×Fijh)-min(Xijh×Sijh)-
(3)
(2)最大完工時間T是車間調(diào)度問題中評價生產(chǎn)效率的重要指標(biāo),如式(4)所示。在動態(tài)調(diào)度中需要對機器故障的修復(fù)時間進行考慮,機器正常工作情況下各工序的加工結(jié)束時間如式(5),機器故障情況下各工序的加工結(jié)束時間如式(6)所示。
T=maxFijh
(4)
Fijh=Sijh+Pijh
(5)
Fijh=Sijh+Pijh+Rh
(6)
(3)機器總負(fù)荷L是零件在機器上加工的總時間,機器總負(fù)荷對機器壽命產(chǎn)生嚴(yán)重影響。
(7)
(4)產(chǎn)品質(zhì)量穩(wěn)定性指數(shù)Q是制造業(yè)企業(yè)生存的命脈,不同的機器生產(chǎn)出的產(chǎn)品質(zhì)量不同,可以用不合格品率表示,不合格品率越低,加工質(zhì)量越穩(wěn)定。加工后期出現(xiàn)產(chǎn)品質(zhì)量問題的成本要遠(yuǎn)高于前期,因此用工序質(zhì)量不穩(wěn)定指數(shù)aijh來表示,如式(8)所示。
(8)
另外,MaO-GDFJSP需要滿足的約束條件如下:
Fijh×Xijh=Sijh×Xijh+Pijh
(9)
(10)
Fijh≤Si(j+1)h
(11)
Fxyh×Xxyh≤Sijh×Xijh,(Sijh≥Sxyh)
(12)
Fijh×Xijh≤Sxyh×Xxyh,(Sijh≤Sxyh)
(13)
FTh=max(Xijh×Fijh)-FMh
(14)
其中,式(9)表示工件一旦加工中途不能中斷;式(10)表示每道工序只能被加工一次;式(11)表示表示同一工件的不同工序之間有先后順序;式(12)和式(13)表示同一時刻,一臺機器只能加工一個工件;式(14)表示一臺機器加工完本機器所有任務(wù)的提前關(guān)機時間。
3 高維多目標(biāo)動態(tài)柔性作業(yè)車間調(diào)度問題的IMOGWO算法
3.1 多目標(biāo)優(yōu)化問題描述
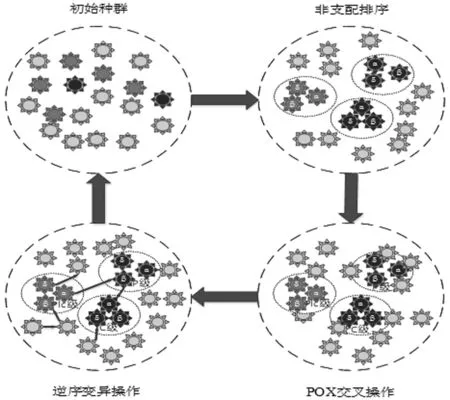
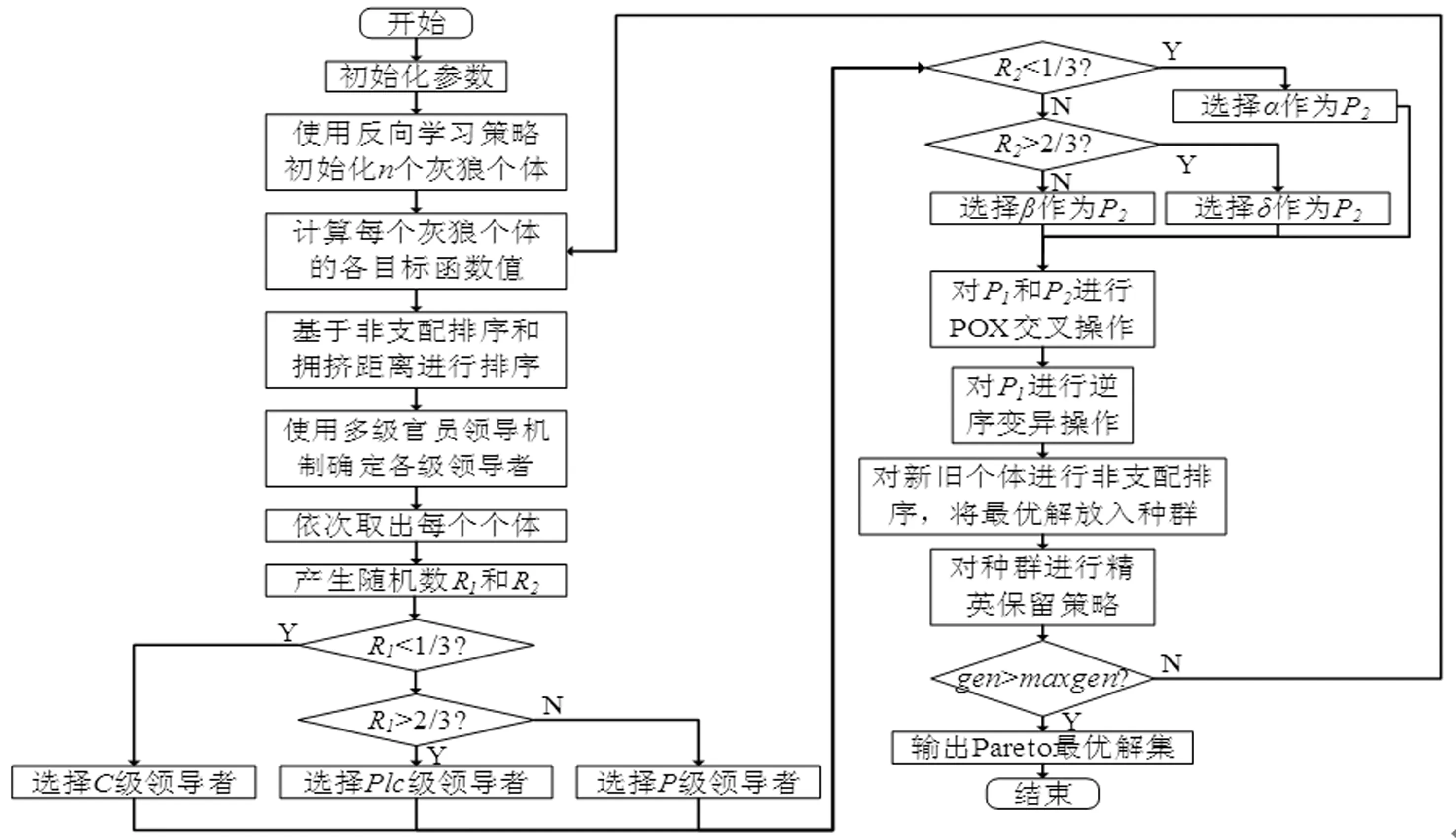
多目標(biāo)優(yōu)化問題(Multi-objective Optimization Problem, MOP)是在多個目標(biāo)函數(shù)F=(f1,f2,…,fr)下求解決策變量X=(x1,x2,…,xm),MOP往往包含多個相互沖突的目標(biāo)函數(shù),故其最優(yōu)解變?yōu)榘鄠€決策變量的最優(yōu)解集。對于給定向量X,Y∈R,當(dāng)且僅當(dāng)?j∈{1,2,…,m},xi 3.2.1 MSOS編碼 染色體編碼會影響優(yōu)化算法的求解效率,本節(jié)選取MSOS[13]編碼方法。此方法將個體分為機器選擇串(Machines Selection, MS)和工序選擇串(Operations Sequence, OS),分別用以解決路徑子問題和調(diào)度子問題,如圖1所示。MS和OS的長度均為總工序數(shù),MS按工序編號依次排列,每個基因座由該工序可選機器集的順序號表示,如工序O22的機器集有{M1,M2,M3},2表示此機器集中第二個機器M2。OS用工件號進行表示,工件i出現(xiàn)的第j次,表示工序Oij。 圖1 MSOS編碼示意圖 3.2.2 反向?qū)W習(xí)初始化種群策略 3.2.3 多級官員領(lǐng)導(dǎo)機制 由于標(biāo)準(zhǔn)GWO算法容易陷入局部最優(yōu),依據(jù)多目標(biāo)優(yōu)化算法最優(yōu)解的特點提出多級官員領(lǐng)導(dǎo)機制,改善標(biāo)準(zhǔn)GWO算法中一級多層的結(jié)構(gòu),進而擴大種群多樣性。多級官員領(lǐng)導(dǎo)機制引入國家(Country)、省(Province)和地級市(Prefecture level city)的政治組織結(jié)構(gòu),每一級均設(shè)有α,β和δ層。從高到低依次為C級、P級和Plc級,每一級內(nèi)α>β>δ,如圖2所示。確定各級領(lǐng)導(dǎo)的具體操作步驟如下: 圖2 多級官員領(lǐng)導(dǎo)機制更新示意圖 Step1對Pareto解集不斷進行非支配排序并反向標(biāo)號; Step2對每一層Pareto解,計算擁擠距離并再次標(biāo)號; Step3從第一層Pareto解集開始,按標(biāo)號依次將灰狼個體取出,直到滿足9個個體; Step4將9個個體依次分配到Cα、Cβ、Cδ、Pα、Pβ、Pδ、Plcα、Plcβ和plcδ,將剩余個體作為ω層。 3.2.4 POX交叉 交叉算子能夠探索未知空間,擴大種群多樣性,起到全局搜索的作用。本節(jié)采用POX交叉算子[15],染色體進行POX交叉操作后仍是可行解,大大提高了算法求解效率。以3個工件,每個工件3道工序為例,如圖3所示,POX交叉算子的操作步驟如下: Step1將兩條染色體作為父代,記為P1和P2,將兩條空染色體作為子代,記為C1和C2; Step2將所有工件隨機劃分到兩個集合中,記為J1和J2,并滿足J1∪J2和J1∩J2=?; Step3將P1和P2中的J1元素分別復(fù)制到C1和C2中的對應(yīng)基因位; Step4將P1中的J2元素依次復(fù)制到C2的空基因位,將P2中的J2元素依次復(fù)制到C1的空基因位上,并調(diào)整加工機器。 圖3 POX交叉示意圖 3.2.5 逆序變異算子 在算法迭代后期,對個體進行逆序變異操作能夠保留父代的優(yōu)秀基因,增強搜索精度,改善算法的局部搜索能力。逆序變異的操作步驟為:首先,選擇一條染色體P;然后,隨機選擇兩個基因位,將兩個基因位之間的所有基因取出并翻轉(zhuǎn);最后插入到基因位斷裂處。 3.2.6 改進精英保留策略 根據(jù)多目標(biāo)優(yōu)化算法最優(yōu)解集的特點,提出改進的精英保留策略。IMOGWO每一代的求解結(jié)果為Pareto最優(yōu)解集,對其循環(huán)進行非支配排序,直到最后一層所有解互不占優(yōu),從后往前對每一層最優(yōu)解集進行標(biāo)號。傳統(tǒng)精英保留策略采用固定比例對種群進行保留,改進的精英保留策略使用自適應(yīng)機制,保留每代種群的前k層Pareto最優(yōu)解集,使用反向種群初始化策略生成g個個體,保持種群規(guī)模不變,k和g的公式如下,其中?x」表示對x向上取整,N為種群規(guī)模,gen為當(dāng)前迭代次數(shù),maxgen為最大迭代次數(shù)。 (15) (16) 為解決高維多目標(biāo)離散型問題,對標(biāo)準(zhǔn)GWO算法進行改進。改進之處主要包括:離散型編碼、反向?qū)W習(xí)初始化種群策略、POX交叉算子、逆序變異算子、多級官員領(lǐng)導(dǎo)機制以及精英保留策略,IMOGWO算法流程如圖4所示。 圖4 IMOGWO算法流程圖 為驗證IMOGWO算法求解MaO-GDFJSP的性能,設(shè)計兩組實驗。第一組在OR-Library中選取11個經(jīng)典的作業(yè)車間調(diào)度測試數(shù)據(jù)集進行求解。相關(guān)參數(shù)設(shè)置為:機器空載功率為[1,10]的隨機數(shù),機器加工功率為[10,30]的隨機數(shù),工序質(zhì)量不穩(wěn)定性指數(shù)為[0,0.3]的隨機數(shù)。第二組實驗對某加工車間的加工數(shù)據(jù)進行仿真,驗證IMOGWO算法求解MaO-GDFJSP的有效性。選取多目標(biāo)粒子群算法MOPSO和未改進多目標(biāo)灰狼算法MOGWO進行對比。為保證對比實驗的科學(xué)性,保持三種算法共同參數(shù)一致:最大迭代次數(shù)maxgen=100,種群規(guī)模n=100,MOPSO算法中的c1=c2=1.4962,w=0.7298,MOGWO算法中的a=2。 為便于比較不同多目標(biāo)優(yōu)化算法的求解性能,采用SP測度和GD測度[16]對三種算法的性能進行評判。測試算例選取3個FT類基準(zhǔn)問題和8個LA類基準(zhǔn)問題。將三種優(yōu)化算法分別對每個測試問題求解20次,每運行一次獲得一組[SP,GD]指標(biāo)值,求SP測度和GD測度的平均值,三種優(yōu)化算法求解結(jié)果如表2所示,每項指標(biāo)的最優(yōu)結(jié)果用粗體標(biāo)識。 表2 11個測試算例的三種算法性能對比 由表2可知,在SP測度方面,IMOGWO算法在10個算例中取得最優(yōu)結(jié)果,表明其相較于另外兩種算法具有很好的分布性,此外MOGWO算法比MOPSO算法分布性要好。在GD測度方面,IMOGWO算法同樣取得10個算例的最優(yōu)結(jié)果,表明三種算法中IMOGWO具有良好的收斂性;相較而言,MOPSO算法的收斂性優(yōu)于MOGWO算法。 運用IMOGWO算法對實際生產(chǎn)企業(yè)車間綠色調(diào)度問題進行求解,引用陳超等[17]中6個工件10臺機器。假設(shè)機器3在30min時發(fā)生故障的加工實例,三種智能優(yōu)化算法分別對其運行20次,求得4個目標(biāo)的最優(yōu)解如表3所示,三種算法求解的甘特圖如圖5所示,Pareto前端四維圖如圖6所示,其中第四維度用顏色表示其大小。由表3可知,IMOGWO算法能夠在總能耗最小情況下保證其他3個目標(biāo)最優(yōu),求解性能優(yōu)于另外兩個算法。而MOGWO算法只在機器總負(fù)荷方面優(yōu)于MOPSO算法。表3表明改進后的IMOGWO算法在高維多目標(biāo)問題的求解上性能更優(yōu)。 表3 三種算法求解MaO-GDFJSP結(jié)果表 (a)IMOGWO求解甘特圖 (b)MOGWO算法求解甘特圖 (c)MOPSO算法求解甘特圖圖5 三種算法求解的甘特圖 圖5(a)~(c)表示三種算法求解MaO-GDFJSP實例的加工方案,不同顏色代表不同的工件,紅線表示在30分鐘時機器3發(fā)生故障,后續(xù)工序需進行重調(diào)度。對比圖5(a)~(c)可知,在總能耗、最大完工時間、機器總負(fù)荷及產(chǎn)品質(zhì)量穩(wěn)定性方面,IMOGWO算法比MOGWO算法和MOPSO算法分別提高(12.6%,13.3%,1.6%,11.5%)和(4.5%,6.6%,2.1%,7.7%),進一步說明IMOGWO算法求解高維多目標(biāo)問題的優(yōu)越性,能夠保證每個目標(biāo)達(dá)到最優(yōu)。 (a)IMOGWO前端 (b)MOGWO前端 (c)MOPSO前端圖6 三種算法的Pareto前端四維圖 圖6(a)~(c)是三種算法Pareto最優(yōu)解集的可視化,能夠?qū)Χ嗄繕?biāo)算法的求解性能進行直觀比較。對非劣解分布性進行分析,對比圖6(a)~(c),IMOGWO算法非劣解的分布性最優(yōu),非劣解沿著Pareto前端均勻伸展,MOGWO算法求得的非劣解在L<190區(qū)域的分布極不均勻,MOPSO算法非劣解的分布性最差,在L<190和T<70的區(qū)域非劣解數(shù)量極少且分布離散,MOPSO算法易進入局部最優(yōu)困境,與表2結(jié)論一致。由此得出,IMOGWO算法在處理高維多目標(biāo)問題時能夠求解更多非劣解,并且Pareto前端的分布性更好。 在綠色智能制造背景下,本文分析了不同機器狀態(tài)下的能耗情況和機器使用節(jié)能方法,以總能耗、最短完工時間、機器總負(fù)荷和產(chǎn)品質(zhì)量穩(wěn)定性為優(yōu)化目標(biāo),建立基于綠色調(diào)度和動態(tài)調(diào)度的MaO-GDFJSP模型,并設(shè)計IMOGWO算法進行求解。該算法以標(biāo)準(zhǔn)GWO算法為基礎(chǔ),使用MSOS編碼以求解離散型問題。用反向?qū)W習(xí)初始化種群策略擴大種群多樣性,引入POX交叉和逆序變異算子對灰狼個體進行更新,創(chuàng)造性地提出了基于多級官員領(lǐng)導(dǎo)機制,設(shè)計自適應(yīng)精英保留策略,使之適用于多目標(biāo)優(yōu)化算法,能夠增強算法的收斂性。 本研究結(jié)論得到管理啟示:(1)算法應(yīng)用方面,提出的IMOGWO算法通過工序合理排序同時優(yōu)化多個目標(biāo),可為企業(yè)生產(chǎn)作業(yè)提供綠色排產(chǎn)方法,實現(xiàn)企業(yè)向低耗能和智能化的現(xiàn)代化生產(chǎn)轉(zhuǎn)變。(2)算法升級方面,“多品種,小批量,低耗能”已成為企業(yè)綠色生產(chǎn)的特點,制造企業(yè)現(xiàn)有的排產(chǎn)算法也需改進升級。因此可基于本文算法改進思路開發(fā)出更符合實際生產(chǎn)的排產(chǎn)系統(tǒng),為制造企業(yè)綠色智能化轉(zhuǎn)型升級賦能。(3)成果推廣方面,近年來,為了應(yīng)對日益加劇的環(huán)境問題,我國政府不斷出臺碳排放相關(guān)政策,如碳交易、強制減排、碳稅制度等[18]。企業(yè)在關(guān)注生產(chǎn)制造過程節(jié)能減排的同時,可以將IMOGWO算法思想應(yīng)用到綠色產(chǎn)品研發(fā)、管理服務(wù)等制造活動各個環(huán)節(jié),實現(xiàn)產(chǎn)品全生命周期“綠色化”和“智能化”雙升級。3.2 改進多目標(biāo)灰狼優(yōu)化(IMOGWO)算法設(shè)計



3.3 改進多目標(biāo)灰狼優(yōu)化(IMOGWO)算法的實現(xiàn)
4 仿真實驗與分析
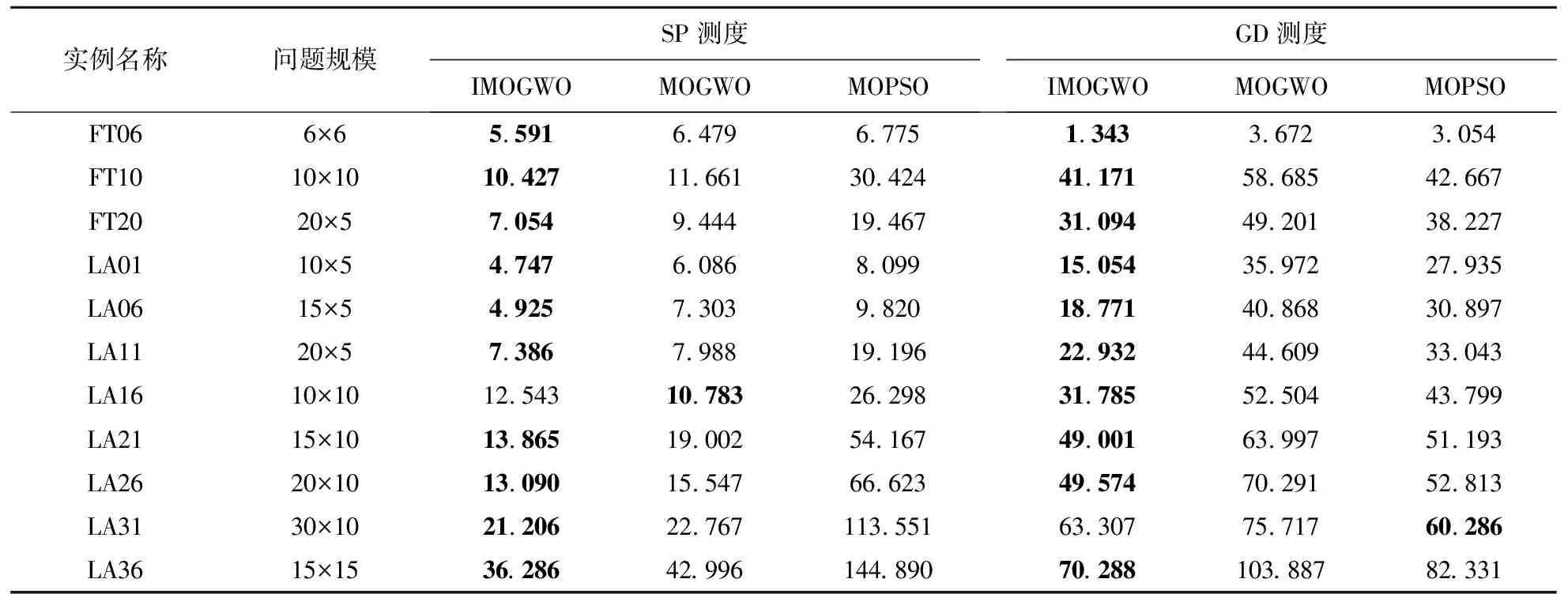
4.1 標(biāo)準(zhǔn)算例仿真實驗結(jié)果及分析
4.2 MaO-GDFJSP仿真結(jié)果及分析



5 結(jié)論與啟示

