資源受限下森林火災應急救援多目標調度優化

王路兵, 吳 鵬, 胡 鵬, 儲誠斌, 李慧嘉

(1.福州大學 經濟與管理學院,福建 福州 350108; 2.北京郵電大學 理學院,北京 100876)

0 引言

21世紀以來，受全球變暖的影響，各種自然災害頻繁發生，給社會造成了嚴重的損失，特別是森林火災。如2019年四川涼山的森林火災、2020年美國加利福尼亞州和澳大利亞的特大森林火災，其中澳大利亞的森林火災造成28人死亡以及30億動物死亡[1]。面對突發大規模森林火災，如何在最短時間內組織科學、高效、快速的應急救援行動，合理調度安排消防救援車輛，用最短時間和最低成本撲滅森林火災具有重要的現實意義[2]。

目前，針對災害發生后的應急救援問題，國內外研究學者已經進行了大量的研究，如王妍妍和孫佰清[3]考慮災害發生后不同階段不同物資的需求與供給關系，提出多災點、多階段的應急物資分配模型，目的是使救援物資的分配成本和延遲成本最小。劉揚等[4]考慮救災物資的需求不確定，提出多階段救援物資調度模型，其旨在盡可能多地分配物資和最小化救援調度總行程時間。呂永波等[5]針對我國夏季部分地區容易發生洪水災害問題，為及時準確地掌握受災情況，減少災情進一步蔓延，構建應急救災物資分配模型，目的是合理分配救援物資和最大化救援效益。Garrido等[6]也考慮了洪水災害問題，并構建最小化救援分配成本的優化模型。針對地震發生后的救援物資分配問題，李雙琳和馬祖軍[7]考慮到震后通往災區交通路網破壞的問題，提出實施交通管制措施，確保應急物資能夠快速有效地送達災區。王付宇等[8]針對地震發生后存在多個救援中心、多個受災區域的情況，提出救援車輛兩階段調度優化模型，目的是使最大救援時間最短和傷員救援權重最大。Hu[9]考慮災后集裝箱多式聯運的應急調度問題，提出多目標整數線性規劃模型，目的是最小化救援車輛的總成本。石彪等[10]考慮大規模突發事件下的應急物資運輸問題，提出兩階段車輛調度模型，目的是最小化應急救援時間。

從以上文獻中，可以發現大多數研究主要集中在對地震、洪災和其它自然災害的應急調度，而對森林火災的研究較少。據本文所知，對森林火災的應急救援調度問題近些年才有相關學者開展研究。如楊忠振等[11]考慮森林火災發生后消防車輛的調度問題，構建同時最小化消防車總運輸時間和運輸成本的雙目標調度模型，并采用免疫克隆算法求解。Tian等[12]針對多起森林火災同時發生后的消防車輛調度問題，構建最小化滅火時間和消防車數量的雙目標優化模型，并采用差分進化算法和粒子群優化算法相結合的算法求解。Wu等[13]在上述研究的基礎上，構建消防資源受限下的雙目標優化模型，并提出動態規劃算法和快速貪婪啟發式算法求解。Ren等[14]考慮資源受限下森林火災應急救援問題，構建以最小化消防救援隊總的行程距離為目標的調度優化模型，并設計一類遺傳算法和粒子群優化算法結合的混合智能算法對模型進行求解。隨后，為有效求解上述資源受限下森林火災應急調度問題，Wu等[15]建立優化模型，采用優化軟件CPLEX求解。最近，吳鵬等[16]對森林火災應急救援問題做進一步研究，考慮多消防車輛的應急救援問題，構建混合整數線性規劃模型，并設計改進人工蜂群算法快速求解模型。

從上述研究可以發現，較少文獻研究了資源受限下森林火災應急救援問題，且尚未有研究報道資源受限下森林火災應急救援多目標優化問題。同時，為減少火災造成的損失，對火災較為嚴重的區域應優先提供消防救援服務，以確保消防救援工作及時、有效的開展。本文根據森林火災發生的特點，提出火勢蔓延模型和滅火時間的計算公式，構建資源受限下多目標調度優化模型，目的是同時最小化消防救援時間和消防車輛總的行駛距離，并提出ε-約束法和模糊邏輯相結合方法對問題進行求解。最后，通過對不同參數下的計算結果進行對比分析，以了解參數變化對消防救援調度方案的影響。

1 森林火災應急調度模型構建

1.1 問題描述

森林火災突發后，消防救援中心需以最短的時間將救援物資送到受災點。但由于森林火災的發生具有很大不確定性，一旦突發大規模火災，消防救援中心的救援資源可能無法同時前往所有的受災點。此時，如何合理地安排消防車輛開展救援工作尤為重要。

為盡快撲滅火災，根據火勢蔓延速度劃分不同的救援優先級，即火勢蔓延速度越大，救援優先級越高，以便有針對性的開展救援工作，其救援過程如圖1所示。從圖1可知，本文主要研究森林火災發生后由救援中心向多個火災點派遣消防車提供救援服務的應急救援問題。同時，探究在消防資源受限下，如何對消防車輛進行合理的調度，從而最小化消防救援時間和消防車總行駛距離。在建立優化模型之前，提出如下假設：

(1)消防車輛的滅火速度大于火勢蔓延速度，確保火災能夠及時撲滅；(2)火災點的火勢蔓延速度、數量以及兩兩之間的距離已知。

圖1 消防救援路線圖

1.2 火勢蔓延模型和滅火時間的計算

火勢蔓延速度受風力、燃料類型、地形坡度等諸多因素的影響，其計算過程的非常困難和復雜的。本文參考文獻[11]的火勢蔓延模型，具體如下所示:

v0=αT+βW+γ

(1)

vs=v0λsλwλφ=v0λsλwλφe0.1782vm

(2)

其中,v0為初始蔓延速度，vs為火勢蔓延速度，其余參數介紹詳見文獻[11]。

(3)

1.3 模型參數與變量

1.4 模型建立

綜上所述，本文構建的多目標優化模型如下:

F1=minCmax

(4)

(5)

(21)

其中，目標函數式(4)為最小化消防救援時間；目標函數式(5)為最小化消防車總行駛距離；式(6)表示每個火災點由一輛消防車服務；式(7)和(8)表示消防車從救援中心出發，在完成滅火后返回；式(9)為流平衡約束；不等式(10)為消防車的行駛時間限制約束；式(11)確保優先級較高的前|K|個火災點優先被消防車救援；式(12)表示救援優先級較高的火災點在救援優先級較低的火災點之前被消防車服務；式(11)和(12)共同確保消防車按火災點的救援優先順序進行滅火；式(13)是消防車的出發時間；式(14)為滅火時間計算公式；式(15)為消防車輛到達火災點的時間；式(16)表示計算消防車的最大救援時間；式(17)和(18)表示每個火災點最多只能被消防車輛服務一次；式(19)～(21)為決策變量約束。

1.5 模型線性化

(1)如果火災點i被消防車輛k服務，則約束式(15)左右合并可以表示如下:

(22)

(23)

(24)

(25)

其中Q是一個非常大的正數。

(26)

綜上，式(15)的兩種可能情況可以由等價線性約束式(24)～(26)共同表示，最終的線性化多目標優化模型可以表示如下:

F1=minCmax

s.t.(6)～(14)、(16)～(21)和(24)～(26)

模型經過線性化處理之后，能夠降低計算方面的困難，并且對比非線性模型，能夠更加快速求解。

2 基于ε-約束迭代和模糊邏輯相結合的算法

為了便于研究，本文將提出的多目標優化模型表示如下:

minF(x)={F1(x),F2(x)} s.t.x∈X

其中，x和X分別表示由約束式(6)～(14)、(16)～(21)和(24)～(26)形成的解向量和可行的解空間；F1(x)和F2(x)分別表示消防救援時間和消防車輛總的行駛距離；{F1(x),F2(x)}表示目標空間。

由于本文研究的兩個目標最小化消防救援時間和消防車輛總行駛距離存在矛盾關系。因此，不存在單一的最優解使得F1和F2最優，而是一組Pareto解使其達到最優。對于本文優化的兩個目標函數F1和F2而言，如果存在一個解向量x*，對于任意x，有F1(x*)≤F1(x)和F2(x*)≤F2(x)，且至少一個不等式是嚴格成立的，則稱解向量x*為非支配解，即Pareto解。所有Pareto解可以在坐標系上形成Pareto前沿面，Pareto前沿面上的點不存在支配關系，并且這些Pareto點可以幫助決策者在F1和F2兩個目標上做出權衡。

目前，通常采用加權法、目標法以及ε-約束法求解多目標優化問題，其核心思想是將多目標問題轉化為一系列的單目標問題，從而獲得一組Pareto解。對比三種方法，ε-約束法比前兩種方法是更適用的，其避免了對目標函數進行縮放和設置適當權重的困難，但是ε-約束法不能幫助決策者在一組Pareto解中快速地找到最優解，而模糊邏輯技術可以幫助決策者尋找最優解。因此，本文提出ε-約束法和模糊邏輯相結合的算法對模型進行求解，不僅可以精確求解本文提出的多目標優化模型，還可以幫助決策者根據自身偏好選擇最優解。基于ε-約束法和模糊邏輯相結合的算法步驟如下:

首先，本文經過分析，將作為主要優化目標，作為ε-約束條件，經ε-約束法轉化后的模型如下:

F1=minCmax

s.t.F2≤ε

Eqs.(6)～(14)、(16)～(21)和(24)～(26)

εk=F2(εk-1)-Δ

(27)

(28)

其中，μ1和μ2分別對應兩個目標函數F1和F2的權重，即決策者對F1和F2的偏好，并且μ1+μ2=1。

3 算例分析

3.1 實例分析

本文以2010年中國大興安嶺山呼中地區發生的森林火災案例進行研究[11]，這次森林火災一共導致7處火災點的發生。由于消防資源受限，消防救援中心只能安排3輛消防車對火災點進行滅火。通過信息技術可以已知火災點之間的距離、位置和火勢蔓延速度，詳細數據詳見參考文獻[11]。

本文通過對消防車輛的相關參數進行設置，以了解參數的改變對消防調度方案的影響。為此，本文擬定以下四種方案撲滅森林火災，如表1所示。此外，還考慮了對兩個目標函數設置不同權重下產生的實驗結果，以便決策者更好地做出決策。四種方案中消防車輛的出發時間為0，然后采用C++編程同時結合CPLEX求解模型。此外，也采用LINGO求解器求解非線性模型，并與線性化后的模型進行對比，以驗證線性化后的求解優勢。具體實驗結果如下所示:

表1 四種方案的相關參數

表2 四種方案的計算結果

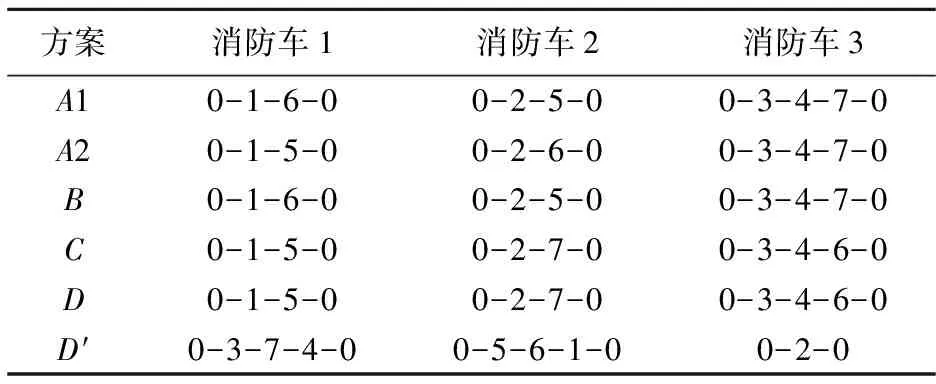
表3 μ1=0.5時消防車最優路徑方案

表2為四種方案的計算結果，K在表2中，表示Pareto解的個數，μ1為目標函數F1的權重，TC和TL分別表示線性化模型和非線性模型的計算時間，D′是根據表1中D方案中的參數按照真實案例的執行方案得出的計算結果。表3為表2各個方案中μ1=0.5時所對應的消防車輛最優調度方案，其中，A1和A2表示方案A中μ1=0.5時對應的兩種可行的調度方案，D′是真實案例執行方案下的消防車輛行駛路徑。

文獻中真實案例的執行方案采用的是就近救援原則，即對距離救援中心距離近的火災點先進行救援，然后再對其它火災點進行救援，目的是最小化消防車輛總行駛距離。如表2所示，雖然就近救援原則在一定程度上降低了消防車輛的行駛距離，但是卻大大增加了滅火救援時間，從而造成大量的資源損失。與真實案例的執行方案不同，本文首先對每個火災點進行救援優先順序的劃分。同時，考慮到消防救援時間問題，并建立多目標優化目標，目的是同時優化消防救援時間和消防車輛總的行駛距離。對比真實案例的計算結果，本文模型的求解結果雖然使消防車輛總的行駛距離增加了，但是與救援時間對比，能夠極大地降低消防救援時間，比真實案例降低了約45.99%。

此外，根據表2和表3的結果：(1)對比方案A和B，如果消防車輛的最大行駛時間較長，則會有更多的消防調度方案，如A有2種可行的調度方案，而B卻有5種；(2)對比方案B和C，消防車的滅火速度對救援時間影響很大，如在方案B中滅火救援時間需要14.55小時，而方案C只需7.19小時；此外，如果方案C在救援過程中實際滅火速度從10米/分鐘降到8米/分鐘，繼續按照表3中的救援方案調度，那么救援時間將會從7.77小時增加至18.22小時，會造成大量森林資源損失，而如果選擇B方案進行救援，那么救援時間將會從7.77小時增加至15.30小時，相比較而言，降低了消防救援時間；(3)同時，對比方案C和D可知，消防車行駛速度越高，救援時間越短，如在方案C中滅火救援時間只需7.19小時，而方案D卻需要9.70小時，同時對消防車輛行駛距離也會有所影響；(4)此外，根據表3中C和D兩種救援方案可知，當實際消防車輛行駛速度從54千米/小時降到40千米/小時，不會影響到消防救援方案，但會明顯增加滅火救援時間；(5)根據表2可知，線性化后模型求解時間明顯比非線性模型求解時間更短。

3.2 仿真算例分析

表4 4輛消防車的計算結果

表5 μ1=0.5時4輛消防車的最優路徑

表6 5輛消防車的計算結果

表7 μ1=0.5時5輛消防車的最優路徑

派遣消防車數量為4和5時，對應的實驗結果如表4和表6所示，其中權重μ1=0.5時，對應的最優消防路徑如表5和表7所示。

根據表4、表5、表6和表7的計算結果可知：(1)消防救援資源會對消防救援時間以及消防車輛的行駛距離產生較大影響，消防救援資源越多，產生的可行調度方案越多，不僅如此，隨著消防車數量的增多，滅火救援時間明顯減少；(2)對比表4和表6，消防車數量的增加會導致計算時間的增加，同時也會加大消防車輛總行駛距離；(3)考慮不同權重時，會對消防車輛調度產生很大影響，當權重μ1=0.1時，兩種消防調度的最大滅火時間相同，此時安排4輛消防車具有更好的消防調度效果；此外，如表6和表7所示，消防車數量不同，對應的最優行駛路徑也不相同；(4)實驗結果表明，線性化模型均能夠在不到一分鐘內得到解決方案，這能實現森林火災發生后第一時間內給出最優的消防調度方案，而非線性模型在10分鐘限制時間內無法獲得求解結果，說明本文提出的線性化模型能夠加快求解速度。

4 結論

本文研究了資源受限下森林火災應急救援問題，構建最小化消防車總行駛距離和消防救援時間的多目標優化模型，并提出ε-約束法和模糊邏輯相結合的算法對模型進行求解。綜合分析了消防車輛的行駛速度、滅火速度、最大行駛時間和消防車數量的變化對消防調度方案的影響，并得出以下結論：(1)在森林消防滅火過程中，消防車輛總的行駛距離會影響到消防救援時間，在實際的消防滅火過程中需要同時考慮到消防滅火車輛總行駛距離與總滅火救援時間之間的關系，以便盡快撲滅火災；(2)在應急救援過程中，為了降低森林資源損失，減少滅火時間，可以考慮事先增加消防資源的配備，如消防車的數量；(3)消防車輛的滅火速度可以在很大程度上減少滅火救援時間，決策者可以在森林火災還未發生時，加強消防滅火設備的配置。

后續將進一步研究森林火災的火勢蔓延速度動態變化對消防調度方案的影響，以及考慮存在多個消防救援中心、多個火災點的研究情況。此外，本文研究森林火災救援問題并沒有考慮到消防救援中心的選址問題。事實上，消防救援中心的選址直接關系到森林火災發生后，能否快速有效地將消防資源送至火災點，進行消防救援。因此，在接下來的研究中，也可以研究消防救援中心選址問題，并結合森林火災發生頻率確定最優選址位置，以確保盡快撲滅森林火災，降低森林資源的損失。