基于控制工序性質的LOB截止日期問題分析與算法

張立輝, 戴谷禹, 鄒 鑫, 乞建勛

(1.華北電力大學 經濟與管理學院,北京 102206; 2.華北電力大學 經濟管理系,河北 保定 071003)

0 引言

重復性項目是指在工程的各個單元和工序之間不斷重復進行施工的一類工程項目[1]，包括公路、管道、橋梁和高層建筑等，涵蓋了絕大多數的工程建設項目。由于重復性項目建設周期長且投資總量大，有效的計劃和調度對于該類項目的順利建設具有十分重要的意義[2]。關鍵路線法(critical path method, CPM)雖然是最常用的項目調度工具[3]，但在處理重復性項目時卻存在許多不足，例如無法保證工作連續性、無法調度多工作隊、更新繁瑣等[4,5]。因此，現有研究提出了一些更適用的調度方法，如平衡線法(LOB，Line of Balance)[6]、線性調度法(LSM，Linear Scheduling Method)[7]和重復性調度法(RSM，repetitive scheduling method)[8]等。其中LOB方法最為常用，該方法采用時間和位置兩個坐標將重復性項目表述為一個二維圖示，以便項目管理者對進度計劃的實際控制。

截止日期問題是重復性項目調度研究中最受關注的問題之一，其旨在不超過給定截止日期前提下求得一個項目工作隊雇傭總量最小的調度方案[9,10]。現有研究在LOB方法框架下設計了一系列有效的截止日期問題求解算法，如CPM/LOB[11]，RUSS[12]，ALISS[13]，HLOB[9]和SHLOB[9]。其中，CPM/LOB方法結合了CPM和LOB各自的特點，旨在快速生成一個滿足截止日期約束的調度方案；RUSS和ALISS方法通過不斷調整工序的工作隊數量來生成有效的截止日期問題進度計劃；HLOB和SHLOB方法則在搜索過程中增加了尋優策略。文獻[10]通過模擬仿真比較了上述幾種方法之間求解效果的差異。還有一些研究則將LOB截止日期問題建立為整數規劃模型進行求解[9，14]。

上述研究中的方法大多為啟發式方法，能夠獲得一個較優的調度方案，但通常不能得到精確的最優解。由于重復性項目往往為大型工程項目，一個準確的最優進度方案能夠節省大量成本，而目前關于截止日期問題精確算法的研究仍然空缺。另外，上述研究缺少對截止日期問題性質的關注，在設計求解方法時未能充分利用問題的結構特征，導致算法求解效率和效果不夠理想。

關鍵路線是項目調度的基礎，許多調度優化方法都是以關鍵路線為基礎設計的。為了區別于傳統的關鍵路線，通常將能夠決定重復性項目總工期的工序稱為控制工序[7]。相對于關鍵工序，重復性項目中的控制工序具有一些獨特的性質，例如一些控制工序工期延長但項目總工期反而縮短。為此，文獻[15，16]等依據控制工序對項目總工期的影響規律，將控制工序分為正控制工序、逆控制工序和點控制工序三種類型。在控制工序性質的影響下，許多重復性項目調度優化問題能夠表現出一定的規律性結構特征，如最短工期問題[17]、資源均衡問題[18]和網絡分析問題[19]等，從而有助于制定更有效的調度策略。

基于上述研究背景，本文考慮從控制工序性質出發，在LOB方法框架下分析重復性項目截止日期問題的內在結構特征，并以此為依據設計高效的調度優化精確算法，最后通過案例分析驗證理論方法的有效性。

1 基于LOB的截止日期問題模型

1.1 LOB表述

作為一種基于圖形的調度方法，LOB通常采用如圖1所示的二維平面來表述一個重復性項目的進度計劃[2]。其中，橫縱坐標分別代表單元和時間，工序則采用一個向右傾斜的四邊形表示。同時，每一個工序又是由多個工期相同的單元組成，每個單元則由一個小矩形表示。以高層建筑項目為例，建筑的裝修工作可視為一道工序，則每一層的裝修工作可視為該工序的一個單元。

圖1 LOB圖示

執行速率 在重復性項目中，一個工序通常會同時雇傭多個工作隊進行施工，為了保證工作隊施工過程的連續，所有單元需按一定的順序分配給工作隊執行，工作隊則需要在不同的單元之間輪轉施工。對任意工序i，其執行速率ri與單元工期di以及雇傭的工作隊數量xi應滿足如下關系：

ri=xi/di

(1)

基于工序的執行速率，工序內各個單元的開始時間則由式(2)聯系起來。

(2)

其中sij表示第i個工序在第j個單元的開始時間。

確定所有工序的工作隊雇傭數量后，可根據工序間的優先關系構建完整的LOB進度計劃。

1.2 截止日期問題模型

重復性項目的截止日期問題旨在滿足截止日期的前提下求得一個工作隊雇傭總量最小的調度方案。本文根據文獻[14]對截止日期問題的描述，構建其數學優化模型。該問題的目標即為最小化項目工作隊雇傭數量，如式(3)所示，其中m表示項目的工序數量。

(3)

優先關系約束保證了重復性項目的工序在施工過程中不會發生沖突，即一個工序的某一個單元完成后，該單元上的緊后工序才能開始。式(4)表述了這種優先關系約束，其中sik表示工序i在單元k上的開始時間，sjk表示工序i的緊后工序j在單元k上的開始時間。

sik+di≤sjk

(4)

截止日期約束確保項目在指定的截止日期Td內完工。由于重復性項目的總工期通常由最后一個單元的完成時間控制，因此，截止日期約束可如式(5)所示，其中n表示項目的單元數量。

smn+dm≤Td

(5)

通常情況下，重復性項目的建設存在資源約束限制，即每個工序雇傭的工作隊數量應有上限。該約束如式(6)所示，其中upi表示工序i的工作隊雇傭數量上限。

xi≤upi

(6)

2 截止日期問題性質

2.1 控制工序類型與性質

在CPM中，關鍵工序的性質都是相同的，即延長或縮短任意關鍵工序，項目總工期也會相應地發生延長或縮短。但在重復性項目，不同類型控制工序的工期變化對項目總工期的影響卻并不相同。在文獻[15]的基礎上，本文考慮將控制工序分為正控制工序、逆控制工序、開始控制工序和結束控制工序四種類型。

圖2(a)和圖2(b)中的工序j分別代表了典型的正控制工序和逆控制工序，工序i和k則代表了工序j的緊前控制工序和緊后控制工序。正控制工序的特點是與其緊前控制工序的優先關系約束僅在第1個單元處嚴格成立，即sj1=fi1，其中sj1表示工序j在第1個單元處的開始時間，fi1表示工序i在第1個單元處的結束時間。同時，正控制工序與其緊后控制工序的優先關系僅在最后一個單元處嚴格成立，即fjn=skn。同樣，逆控制工序的特點則是與其緊前控制工序的優先關系約束在最后一個單元處嚴格成立，即sjn=fin，與其緊后控制工序的優先關系在第一個單元處嚴格成立，即fj1=sk1。

圖2 正控制工序和逆控制工序

文獻[15]將工序工期變化對項目總工期沒有影響的控制工序定義為點控制工序，本文根據優先關系的不同進一步將點控制工序分為開始控制工序與結束控制工序。其中，開始控制工序的特點是與其緊前控制工序和緊后控制工序的優先關系都在第一個單元處嚴格成立，即sj1=fi1且fj1=sk1，如圖3(a)所示。結束控制工序的特點是與其緊前控制工序和緊后控制工序的優先關系都在最后一個單元處嚴格成立，即sjn=fin且fjn=skn，如圖3(b)所示。

圖3 開始控制工序和結束控制工序

根據上述各類控制工序的特點可以發現，優先關系嚴格成立的單元不變的前提下，在一定范圍內改變控制工序的執行速率不會導致控制工序自身類型發生變化。其中，正控制工序的執行速率在[1/dj,ri]內變化不會導致自身轉變為其他類型的控制工序，逆控制工序執行速率的變化區間為[ri,upj/dj]，開始控制工序執行速率的變化區間為[rk,ri]，結束控制工序執行速率的變化區間則為[ri,rk]。

2.2 工序性質與總工期關系

根據文獻[15]，重復性項目的總工期可由式(7)計算。

(7)

其中Di表示工序i的工期，I1表示正控制工序集合，I2表示逆控制工序集合，I3表示開始控制工序集合，I4表示結束控制工序集合。

單個工序i的工期Di可由該工序的單元數和執行速率計算得到，如式(8)所示。

(8)

將式(8)帶入式(7)中，可得到基于工序執行速率的重復性項目總工期公式，如式(9)所示。

(9)

控制工序的特點表明控制工序的執行速率在一定范圍內變化時其自身類型不變，而項目總工期公式(9)則反映了控制工序執行速率與總工期之間的關系。結合二者可以得到關于控制工序執行速率與項目總工期關系的命題：

命題1若工序j為正控制工序，當工序執行速率rj在[1/dj,ri]內變化時，增加工序執行速率rj，項目總工期減少，減少工序執行速率rj，項目總工期的增加。

證明若工序j為正控制工序，由正控制工序性質，其執行速率rj在區間[1/dj,ri]內變化時不改變自身工序類型。由式(9)可知，執行速率在該區間內變化時，項目總工期隨執行速率rj的增加而減少，隨執行速率rj減少而增加，命題得證。

命題2若工序j為逆控制工序，當工序執行速率rj在[ri,upj/dj]內變化時，減少工序執行速率rj，項目總工期減少，增加工序執行速率rj，項目總工期增加。

命題3若工序j為開始控制工序，當工序執行速率rj在[rk,ri]內變化時，增加或減少工序執行速率rj，項目總工期不變。

命題4若工序j為結束控制工序，當工序執行速率rj在[ri,rk]內變化時，增加或減少工序執行速率rj，項目總工期不變。

命題2、3、4的證明方法同命題1。上述命題闡述了控制工序類型在保持不變的前提下，工序執行速率變化與項目總工期之間的關聯，項目管理者可根據其中的規律更精確地控制重復性項目總工期。

2.3 問題性質

命題1～4建立了控制工序執行速率與項目總工期之間的聯系，由于工序的執行速率是由雇傭的工作隊數量和單元工期決定，因此上述命題本質上建立的是工作隊雇傭數量與項目總工期之間的聯系。由于截止日期問題的目標是求得一個工作隊雇傭數量最少的進度計劃，利用上述命題可得到最優的截止日期問題進度計劃應滿足如下幾個條件。

條件2和3的證明方法同條件1。

上述三個條件揭示了截止日期問題的一些規律，其中，條件1利用了項目總工期公式中逆控制工序具有雇傭工作隊數量和項目總工期同向變化的特點，即工作隊雇傭數量減少項目總工期也減少。條件2和條件3則利用了開始控制工序和結束控制工序工作隊雇傭數量在一定范圍內變化不影響項目總工期的特點。這些性質對于實際工程項目的進度安排具有指導意義，項目管理者可以根據這些性質判斷一個調度方案是否合理。同時，這些性質可以進一步為調度算法的設計提供依據。

3 分支限界算法設計

目前求解截止日期問題的方法主要集中于啟發式算法。啟發式算法通常能夠得到一個較優的可行解，但重復性項目往往投資和建設規模較大，求得精確的最優調度方案對節約項目成本和資源具有非常重要的意義。分支限界算法是一種求解問題精確解的有效算法，其算法流程包括分支、限界和剪枝幾個步驟。基于上述截止日期問題的性質，本文設計了一種具有針對性的分支限界算法實現對截止日期問題的精確求解。

3.1 分支策略

截止日期問題的解空間可由一個樹型結構進行組織，每一層的結點分別對應一個工序的工作隊雇傭數量情況，如圖4所示。每個結點包含了相應的進度計劃信息，包括工序編號，工序單元工期，工作數量等。分支限界算法從根結點出發，不斷選擇當前未分支的結點中目標下界最小的結點作為拓展結點進行分支，分支的數量由工序i的緊后工序j的工作隊雇傭量上限決定。

圖4 解空間圖示

3.2 限界策略

為求得截止日期問題的一個下界，對工序工作隊雇傭數量這一整數變量xi進行連續松弛，并不考慮其資源約束。在該情況下，顯然當所有工序的執行速率都相同且總工期等于截止日期時，項目所需的工作隊數量最少，此時工序的執行速率可由式(10)確定。

r=(m-1)/(Td-T1)

(10)

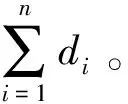
每個工序的工作隊理想雇傭數量可由式(11)計算得到。

ci=diri=(m-1)di/(Td-T1)

(11)

(12)

將式(12)從整體考慮到局部，當某個結點對應的前j個工序的工作隊雇傭數量已確定，則該結點的目標下界估計式如式(13)所示。

(13)

3.3 剪枝策略

剪枝策略是分支限界算法在搜索迭代過程中利用已知的信息判斷結點是否可行或是否有可能成為最優解，若能夠判斷出不可行或不是最優解則刪除該結點以加快算法搜索效率。利用本文提出的截止日期問題性質以及問題固有結構，可以設計出如下三個剪枝策略。

剪枝策略1：若某一節點的項目總工期估計下界fT超過截止日期Td，即fT>Td，應刪除該結點。項目總工期的估計下界可由式(14)計算。

(14)

3.4 算法流程

基于上述分支策略、限界策略和剪枝策略，本文設計的針對截止日期問題求解的分支限界算法步驟流程如下所示：

步驟1建立初始結點并初始化參數；

步驟2選擇下界最小的結點作為拓展結點；

步驟3當沒有結點能夠被選做拓展結點時，算法結束，得到最優解，否則，轉步驟4；

步驟4對當前拓展結點進行分支，并計算子結點參數；

步驟5利用剪枝策略刪除不滿足條件結點；

步驟6標記該拓展結點為已拓展并轉步驟2。

4 算例分析

4.1 計算效果分析

本文選用文獻[9]中的案例驗證算法計算效果的有效性。該項目為一高速公路項目，共包含24個工序和10個單元。利用本文提出的分支限界算法對該案例進行求解，并與CPM/LOB[11]，ALISS[13]和SHLOB[9]三種啟發式算法的計算結果進行比較，其結果如表1所示。

表1 案例計算結果

由表1可知，相對于現有算法，本文提出的分支限界算法能夠得到一個最優的調度方案。CPM/LOB方法雖然都能夠得到一個工作隊雇傭數量較少的調度方法，但是無法滿足截止日期約束，是不可行的。ALISS能夠生成一個滿足截止日期的方案，但是需要雇傭更多的工作隊，項目成本較高。SHLOB方法也得到了問題的最優解，但是該方法實際上引入了隨機搜索機制，計算效果并不穩定。通過數值實驗，使用SHLOB算法求解該案例1000次，僅5次能夠得到最優解，計算效果并不十分理想。

4.2 計算效率分析

進一步分析本文提出的剪枝策略對算法計算效率的影響。依據剪枝策略的選擇，考慮3個版本的分支限界算法。其中，算法1僅使用剪枝策略1，算法2使用剪枝策略1和2，算法3則使用所有剪枝策略。測試算例根據表2的參數設置隨機生成。

表2 算例參數設置

本文采用Microsoft Visual C++實現算法程序，代碼在一個主頻為2.4GHz、內存為4G的個人計算機上運行。測試完所有案例后，采用如下3個指標衡量算法的計算效率：

(1)ACT：算法平均計算時間。

(2)MCT：算法最大計算時間。

(3)NUM：算法遍歷的結點數量。

3個版本算法的計算結果如表3～5所示。從表中可以看出，所有算法的計算時間都隨著案例規模的增加而增加。所有算法中，算法3無論是計算時長還是計算時間增長速度都顯著優于算法1和算法2，即使用所有剪枝函數能夠最大限度提高算法的計算效率。對比直接求解截止日期問題數學模型的計算效率，表6給出了采用Lingo優化求解器求解相同規模案例的計算時間，可見本文提出的分支限界算法計算效率顯著優于Lingo求解器。

從遍歷結點數量看，采用不同的剪枝策略會導致不同的遍歷結果。以工序數量為30時為例，相對于算法1，算法2能夠少遍歷36.6%的結點，而相對于算法2，算法3則能夠少遍歷96.5%的結點。可見，剪枝函數能夠有效的識別非最優解從而加快算法的搜索速率，但是不同的剪枝策略對算法搜索效率的提高程度有所不同。其中，剪枝策略3，即利用逆控制工序和結束控制工序性質的剪枝策略，對計算效率的提升最為顯著。

表3 算法1計算效率

表4 算法2計算效率

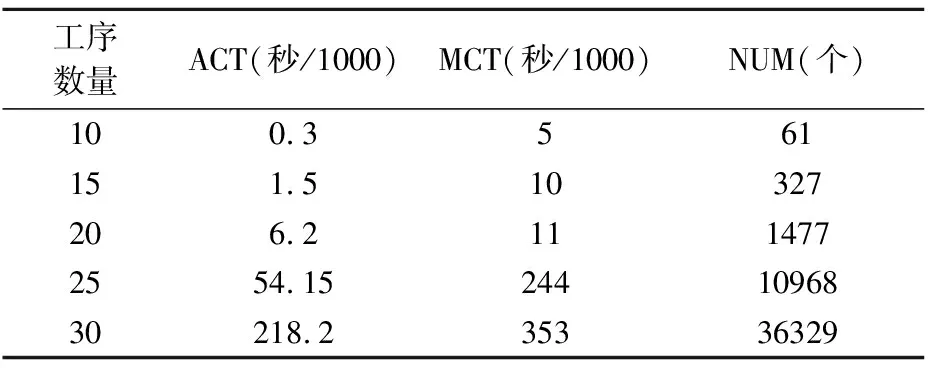
表5 算法3計算效率

表6 Lingo計算效率

5 結論

本文從控制工序性質出發，對重復性項目截止日期問題進行分析。在確定不同類型控制工序穩定區間的基礎上，將重復性項目總工期公式轉換為基于執行速率的動態形式，建立工序執行速率與項目總工期的關系，并推得最優截止日期問題進度方案所需要滿足的條件。項目管理人員可以利用這些性質檢驗一個調度方案是否可行且經濟。進一步地，本文設計了一個具有針對性的分支限界算法，利用所提出的截止日期問題性質設計剪枝函數并整合到算法流程中。算例的計算結果表明本文提出的算法能夠得到問題的精確最優解，且計算效率優于啟發式算法以及模型求解器。

本文研究主要針對的是重復性項目截止日期問題，而對于其他類型的調度優化問題也可能存在類似的性質和特點，如費用優化問題和時間費用權衡問題等。因此，基于控制工序性質分析其他重復性項目調度優化問題的規律特征，并以此設計更有效的調度優化算法是未來非常具有潛力的研究方向。