壓電功能梯度層合梁的力-電-熱耦合梁單元及最優振動控制

柏冬軍，石廣玉

(天津大學力學系，天津 300354)

功能梯度材料是由兩種或兩種以上的材料組成的一種復合材料，其成分及相關的材料特性通常在一個方向或者多個方向呈連續平穩變化[1]。由于其內部材料屬性的連續變化，功能梯度材料可以有效避免普通層合材料因內部材料突變所產生的應力集中問題，因此近些年來由功能梯度材料所組成的結構備受關注[1-5]。近年來結構的振動控制是工程中的熱點問題，尤其在航空航天及汽車領域。通常將壓電材料作為傳感器與致動器粘貼或鑲嵌在柔性結構的表面，通過控制電路實現對結構的振動主動控制。因而，包含壓電傳感器和致動器的智能層合結構的建模、分析以及設計也受到廣泛關注[6]。其中結構的核心層為各向同性材料或層合復合材料的研究文獻最為多見，而智能功能梯度層合結構的有限元建模及其振動主動控制的研究則較少[7-8]。對于包含壓電層及功能梯度層的智能層合結構，壓電層的力電耦合效應會影響到結構的力學響應。合理的層合板理論對準確且高效地進行層合結構的多場耦合分析十分重要。M ITCHELL 和REDDY[9]提出了一個高效壓電層合板分析的雜交板理論，它使用等效單層板理論表征層合板的力學行為，用Layer-w ise理論描述其電勢場。

一個理想的振動控制方法要以較小的能量和較短的時間實現對結構振動的穩定的控制。基于速度反饋的振動控制方法在壓電功能梯度層合結構的振動控制中得到廣泛的應用[10-13]。它通過改變反饋增益的值得到不同大小的控制力實現對功能梯度結構的振動控制。SELIM 等[10]以及YASIN等[8]研究了常增益負反饋控制的穩定性問題，且SELIM等指出由于壓電功能梯度層合結構存在拉彎耦合變形，會使得控制系統變得不穩定，兩篇文獻均通過改變壓電傳感器層和致動器層的位置提升系統的穩定性。劉濤等[13]基于等幾何方法同樣采用常增益負反饋控制研究了功能梯度板的振動控制問題，引入物理中面的概念避免當傳感器與致動器粘貼于功能梯度層表面時由于拉彎耦合效應引起的控制不穩定問題。經典控制方法操作簡單但卻忽略了控制過程中能量的消耗，所得基于系統輸出反饋的控制力往往并非為最優控制力，因而不是最優振動控制。BRUANT 等[7]及HARTI等[14]基于LQR 算法實現功能梯度梁上局部布置壓電片時的振動控制，并討論了壓電致動器和傳感器的位置對結構振動控制效果的影響。YASIN 等[8]基于Layer-w ise理論表述梁內位移場及電勢場，提出了一個帶內部電學自由度的壓電功能梯度梁單元，使用常增益速度反饋控制算法和LQR 算法對結構的振動進行控制。結果表明：LQR 最優控制比常增益負速度反饋控制所消耗能量更低，且LQR 不存在上述穩定性問題。因而，LQR 是實現最優主動振動控制的良好選擇。

壓電功能梯度層合梁具有力-電-熱的耦合效應，故對應有限元模型的計算效率對工程問題的求解很重要。現有的力-電-熱耦合分析有限元都是采用數值積分[8,11,14-15]。TIAN 等[16]的工作表明，采用擬協調元法可以得到層合結構的顯式單元剛度矩陣，從而避免了數值積分和提高了計算效率。基于彈性力學基本方程以及能量等效原理得出的SHI[17]改進的三階剪切變形理論可以精確地考慮橫向剪切變形對梁振動高階頻率的影響。

本文采用雜交板理論[9]和Ham ilton 原理推導壓電功能梯度層合梁的力-電-熱耦合控制方程，其中用SHI[17]改進的三階剪切變形理論描述梁的位移場，用Layer-w ise 理論[9]分層地描述壓電層電勢場。然后用假設應變的擬協調元法[18]推導兩節點壓電功能梯度層合梁單元的剛度矩陣。由于推導過程中單獨假設梁中切應變以及剪切應變梯度，可以有效避免梁單元的剪切自鎖。使用所得力-電-熱耦合梁單元進行了不同載荷下壓電功能梯度層合梁的靜力和動力分析，用LQR 最優控制算法實現了結構振動的主動控制。所得計算結果與其它梁單元結果及二維有限元解的比對驗證了文中所給力-電-熱耦合梁單元的準確性。

1 壓電功能梯度層合梁單元

如圖1所示為一個壓電功能梯度層合梁，梁中間層功能梯度層厚度為hc，它由兩種不同的材料沿梁高度按一定規律梯度分布復合而成。功能梯度上下表面粘貼有等厚度hp的壓電層。假設相鄰兩層理想粘結且不考慮粘結層影響，并只考慮xoz平面內的荷載。

圖1 壓電功能梯度梁示意圖Fig.1 Geometry of piezoelectric functionally beam

1.1 壓電功能梯度梁本構關系

功能梯度層由金屬和陶瓷按一定的規律復合而成，其上側為純陶瓷，下側為純金屬。其等效材料參數，如彈性模量、泊松比、熱膨脹系數、密度等，沿梁厚度方向呈連續均勻變化。陶瓷體積分數Vc沿厚度方向的分布可表征為[10]：

其中，N為功能梯度層材料的組分指數，陶瓷體積分數和金屬體積分數滿足Vc+Vm=1。

研究者提出了許多表征材料性能沿高度梯度變化的細觀力學模型，其中最常用的為Voigt 模型[7,10-13,19]和Mori-Tanaka 模型[8,15]。Voigt 模型簡單易用，可用于預測由常規功能梯度材料組成結構的材料特性和整體響應；而Mori-Tanaka 模型更注重相鄰內含物之間的相互作用[8]。由于Voigt 模型操作簡便，其被多數學者用來預測材料性能的變化。Voigt 模型把功能梯度材料的等效材料參數Pf表征為：

式中：Pm為金屬材料的材料參數；Pc為陶瓷材料的材料參數。

功能梯度材料最早用于航空航天領域作為隔熱涂層，其工作環境通常為高溫環境。因此有必要考慮溫度對其的影響。功能梯度材料考慮力-熱耦合的本構方程為：

其中：

式中，功能梯度材料彈性模量Ef和泊松比μ沿厚度方向的分布，可由式(2)得出。

壓電材料考慮力-電-熱耦合的三維本構關系為：

其中，σ 和ε 分別為壓電材料的應力張量及應變張量，而D和E則分別為其電位移矢量及電場強度矢量；C、e、k分別為彈性矩陣、壓電矩陣及介電矩陣；α 及p分別為材料的熱膨脹系數及熱電系數。ΔT=T-T0，T為材料的溫度，T0為參考溫度，在此溫度下，物體處于應力自由狀態。本文假設溫度沿著梁厚度方向線性分布：

式中：Tt、Tb分別為梁上下表面的溫度值；h為梁的高度。

對于正交各向異性壓電材料，其具有三個相互正交的彈性對稱平面，其三維彈性矩陣為：

假設壓電材料為正交晶系壓電晶體，且沿z方向極化，其三維壓電矩陣e、介電矩陣為k：

對圖1所示一維梁模型，假設z方向正應力σ3=0。若其處于平面應力狀態，有σ2=τ12=τ23=0,以及γ12=γ23=0。并且壓電材料只沿著z方向極化，電場分量E1=E2=0。將上述已知值代入材料三維本構方程式(5)中得到梁中壓電層的力-電-熱耦合本構方程：

其中：

1.2 梁內位移場與電勢場

對于橫向剪切變形不可忽略的層合梁，使用等效單層理論計算其位移場可得到較好結果。而壓電層力電耦合效應對結果有一定影響，有必要分層考慮每層壓電層的電勢分布。若其厚度較厚則需在分層考慮的基礎上再次將每層壓電層離散為數個子層。本文擬采用此類基于等效單層理論描述層合結構中位移場分布，基于分層理論描述各壓電離散層電勢場分布的雜交板理論[9]。

1.2.1 Shi 三階剪切變形理論

采用Shi 改進的三階剪切變形理論[17]，平面彎曲梁的位移場可寫為：

式中：u和w分別為梁內的軸向位移及橫向位移；u0和w0分別為梁中面的軸向位移及撓度；為梁橫截面的平均撓度； γx為梁橫截面的剪切變形；h為梁的高度；α=1/4，β=5/3h2。梁橫截面的剪切變形 γx為：

式中：em為膜應變；eb為彎曲應變；es為剪切應變；ehs為剪切應變梯度。它們與位移的關系為：

彎曲項對于梁單元的計算精度至關重要，由式(18)中彎曲應變表達式可知，若建立撓度的三次插值，在單元域內會得到沿軸向線性分布的彎曲應變。相比較在單元域內常彎曲應變的梁單元來說，此單元精度更高。

1.2.2基于Layer-w ise理論的電勢場

基于Layer-w ise理論，本文分層描述梁橫截面上壓電層的電勢的分布。將梁內壓電層沿高度離散，假設壓電離散層數量為m層，則梁中電勢場分布可以表示為[9]：

式中：φj為第j層壓電離散層層間接觸面的電勢分布；Lj(z)則為相應的沿梁高度的插值函數。

若對每一離散層只選取其上下表面電勢值作為電勢場沿z方向離散的節點，則對于第j層壓電層其電勢可由此層上下表面電勢表示為：

1.3 壓電功能梯度梁單元的能量泛函

設壓電功能梯度層合梁中壓電層數量為m，總鋪層數量為n，則考慮力-電-熱耦合的單元電熱焓為：

式中：下標q 為力學量；下標 φ為電學量；下標θ為熱學量；Ωe為單元的體積。從式(22)可以看出，梁的勢能主要包括應變能Uqq、壓電能Uφq及Uqφ、電勢能Uφφ以及力熱耦合能量Uθq、熱電耦合能量Uθφ。式(22)中應變能部分為：

1.4 壓電功能梯度層合梁單元

本節將以撓度及橫向剪應變作為基本場變量的位移場和以壓電層層間電壓作為基本未知量的電勢場推導一個如圖2所示的兩節點C1連續梁單元。單元節點位移及電勢向量為：

圖2 兩節點壓電功能梯度梁單元Fig.2 Two-noded piezoelectric functionally graded beam element

1.4.1基于擬協調元法推導單元應變矩陣

傳統以位移為基本未知量的有限元法,單元的應變矩陣基于位移應變關系得出。而以擬協調元法推導單元剛度矩陣則通過直接假設單元的應變場，以弱形式使得協調方程得到滿足[18]。則式(23)單元應變能變為：

得到各應變分量插值為：

1.4.2單元剛度矩陣

將式(40)應變插值代入式(23)單元應變能中，可得單元的力學剛度矩陣：

其中：

式中：

式中：A11為拉伸剛度；B11為拉彎耦合剛度；D11為彎曲剛度；E11、F11和H11為與高階剪切相關的項。

對于第j層壓電層，其壓電層層間電勢差為：

其中：

將式(44)代入式(27)所示電勢能可得電學剛度矩陣：

綜上所述，單元剛度矩陣為：

1.4.3單元的一致質量矩陣

由式(15)位移場的表達式對時間求導可以得到速度場的分布：

將之代入到動能表達式可得：

其中：

代入相應的速度場插值，對動能變分可得單元的質量矩陣M qq：

式中：M u0、M w0和M wx分別為軸向、橫向和轉動慣量矩陣；Mγ為高階剪切變形所引起的質量矩陣；M uwx、M uγ及M wxγ分別為不同慣量之間的耦合項；N u0、N w0、N wx及Nγ分別為相應分量的速度場插值。

1.4.4單元有限元列式將應變插值代入力-熱耦合能式(29)及電-熱耦合能式(31)，可得由溫度荷載導出的荷載向量Fθq和Fθφ：

若假設梁承受均布荷載f，且第j層壓電層上下表面電荷密度為Q={Qj+1Qj}T，上下表面電勢為φj={φj+1(x,z j+1,t)φj(x,z j,t)}，系統外力及電荷做功為：

將如上所述單元勢能Ue、動能Te和外力功We對所有單元求和得到系統整體的勢能U、動能T及外力功W代入到Lagrange 方程中即可得到系統的運動方程：

求解式(57)可得壓電功能梯度梁在力電熱耦合荷載作用下有限元方程：

2 基于LQR 的最優振動控制

2.1 動力系統的狀態方程

在圖3所示振動控制系統中，外加激勵下梁產生振動并在壓電傳感器中產生電壓。在接收到動力系統輸出電壓后，控制系統將反饋信號傳入致動器并在其上產生控制電壓抑制梁的振動。

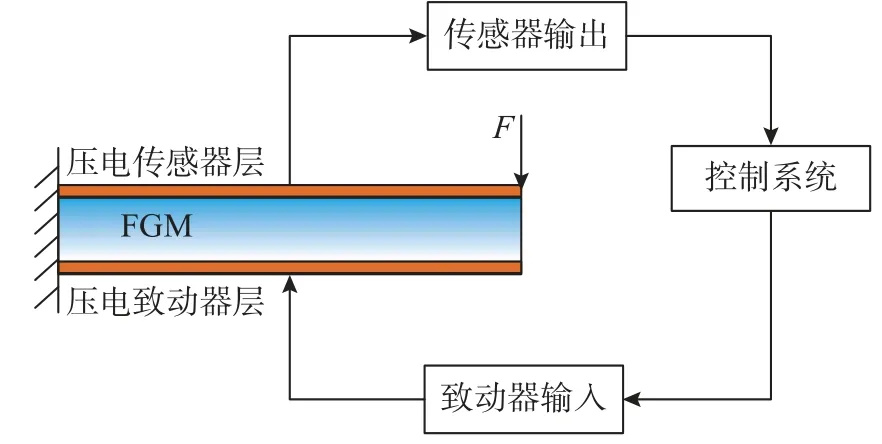
圖3 動力系統模型Fig.3 Model of the dynam ic system

若考慮系統Rayleigh 阻尼可得到壓電功能梯度梁強迫振動方程：

其中：

式中，a和b為Rayleigh 阻尼系數。

若取動力系統前mr階振型在模態空間下求解壓電功能梯度梁的動力響應并對其進行振動控制。如式(61)所示強迫振動方程，令外加荷載為零可求其自由振動頻率ωi及模態 φi。系統響應可由前mr階振型表示為：

其中：Φ 為系統振型矩陣；η 為系統的模態坐標向量。將式(64)代入式(59)，得到系統在模態坐標描述下運動方程為：

式中，I、Λ 和Ω分別為正則化之后的質量矩陣、阻尼矩陣和剛度矩陣。

對動態系統的控制通常在狀態空間下描述，本文以模態坐標及其對時間的一階導數為狀態變量，X(t)=，以傳感器層電壓及其一階導數為輸出變量Y(t)=可得動力系統的狀態空間表達式：

式中：uq和uφ為系統的輸入變量，分別表示外部施加力向量以及用于控制壓電功能梯度梁的振動外部輸入電壓；A和C為系統的狀態矩陣及輸出矩陣；Bq和Bφ分別為系統的力學及電學輸入矩陣。各變量及矩陣的具體形式為：

2.2 基于LQR 的最優振動控制

采用二次型最優控制算法求解最優控制力，系統性能指標泛函為：

式中：Q x為狀態變量的加權矩陣，其為正定或半正定矩陣；R為系統輸入變量的加權矩陣，其為對稱正定矩陣。

在約束條件式(66)下，可使用拉格朗日乘數矩陣P(t)構造如下的拉格朗日函數[16]：

將uφ(t)作為自變量對性能指標泛函求變分得到：

求解式(70)可得反饋控制電壓uφ(t)：

式中，GA為最優狀態反饋增益矩陣。拉格朗日乘數矩陣P由如下Riccati 方程得：

根據現代控制理論，對于無限時間狀態調節器P為常數矩陣，則式(72)轉化為代數方程。此方程可使用MATLAB控制系統工具箱中lqr函數進行數值求解。將式(71)最優控制力代入原狀態方程式(66)之中得到閉環控制系統的狀態方程：

3 數值算例

3.1 壓電功能梯度層合梁在不同載荷下的靜力響應

為了驗證文中提出的力-電-熱耦合梁單元的計算精度，考慮壓電功能梯度層合梁在不同載荷下的靜力響應。此算例不僅考慮位移的計算結果，也考慮應力計算結果。主要為如下三種荷載：

荷載1，機械載荷：梁受均布荷載q=-5 kN/m，壓電層為閉路邊界條件[15]，即：

荷載2，電場載荷：壓電層與功能梯度層接觸面接地，梁上下表面施加電壓[15]，即：

荷載3，溫度載荷：梁上表面溫度為100℃，下表面溫度為0℃，并假設溫度為0℃材料處于應力自由狀態[19]。

圖1所示為一個壓電功能梯度層合簡支梁，其長L=250 mm，高度h=5 mm。中間層為由ZrO2及A l 組成的功能梯度層，其高度hc=4mm，上表面為純ZrO2，下表面為純A l，中間其材料參數呈梯度變化。本例采用Mori-Tanaka 方法[15]模擬功能梯度層材料的梯度分布。功能梯度層上下表面粘貼有等厚度的PZT-1195N 壓電薄層。本例所用材料參數為：

將梁劃分為10個單元。表1為梁在均布荷載及電壓作用下梁跨中截面最大位移及最大應力計算結果，圖4為在機械載荷和電荷載作用下梯度指數N=0.25時梁中心截面的正應力分布。YASIN等[15]通過假設電勢場沿高度二次分布，并基于本構方程求解得到可描述高階剪切變形的位移場，提出了一個包含內部電節點的梁單元。其計算結果如表1所示。

表1 兩種荷載下功能梯度簡支梁的撓度和正應力計算結果Table 1 Central deflection and normal stressof simply supported smart FGM beam under two different loads

Ansys計算結果為使用軟件Ansys平面單元計算所得，采用Plane13單元及Plane182單元分別劃分壓電層及功能梯度層的網格。并采用等效分層模型描述功能梯度層中材料參數沿高度的分布，即將功能梯度層分為100層子層，每一子層由各向同性材料組成，其材料常數由Mori-Tanaka模型確定。從表1及圖4可以看出使用本文梁單元與YASIN的高階梁單元及Ansys計算結果基本一致。梁承受均布荷載時隨著核心層梯度分布指數增大，在外荷載作用下梁中心截面撓度及最大彎曲正應力逐漸增大。但在電載荷作用下，梁中心截面的撓度逐漸增大，而其彎曲應力卻逐漸減小，這表明此壓電功能梯度層合梁有很強的力-電耦合效應。

圖4 兩種荷載下梁正應力沿厚度方向變化Fig.4 Through-the-thickness variation of σx under two different loads

為進一步研究梁的力-電-熱耦合效應，本例將考慮如圖3所示壓電功能梯度層合懸臂梁承受沿梁高度方向線性分布的溫度荷載即荷載3。梁的長度為L=200mm，功能梯度層由A l 及ZrO2復合而成，其厚度為hc=30mm。壓電層材料為G-1195N厚度為hp=0.1 mm。本例所用材料參數如下所示：

溫度荷載作用下，不同組分指數的功能梯度材料梁自由端的最大撓度如表2所示。溫度荷載作用下組分指數N=∞ 時梁的撓曲線如圖5所示。采用荷載傳遞法，用Plane55單元劃分壓電功能梯度梁，計算得到沿厚度方向線性分布的溫度場。在相同網格下，使用Plane13單元劃分壓電層網格，Plane182單元劃分功能梯度層網格，施加如前所述溫度場得到梁端最大撓度。表2中基于均勻分層模型將功能梯度層分別劃分為100及200層，使用Ansys計算溫度荷載作用下梁端撓度。使用本文所推導的梁單元計算結果與Ansys計算結果基本一致，與功能梯度層劃分為200層時的結果更為接近。圖5顯示了N=∞時梁在溫度影響下的撓曲線，其中LIEW 等[19]使用的是一階剪切變形的板單元并以壓電層電壓作為節點自由度。從圖中結果可以看到，本文的計算結果比文獻[19]的解與Ansys解(200層的計算結果)吻合的更好。

表2 溫度荷載下梁端撓度Table 2 Tip deflectionsof beam under temperature load

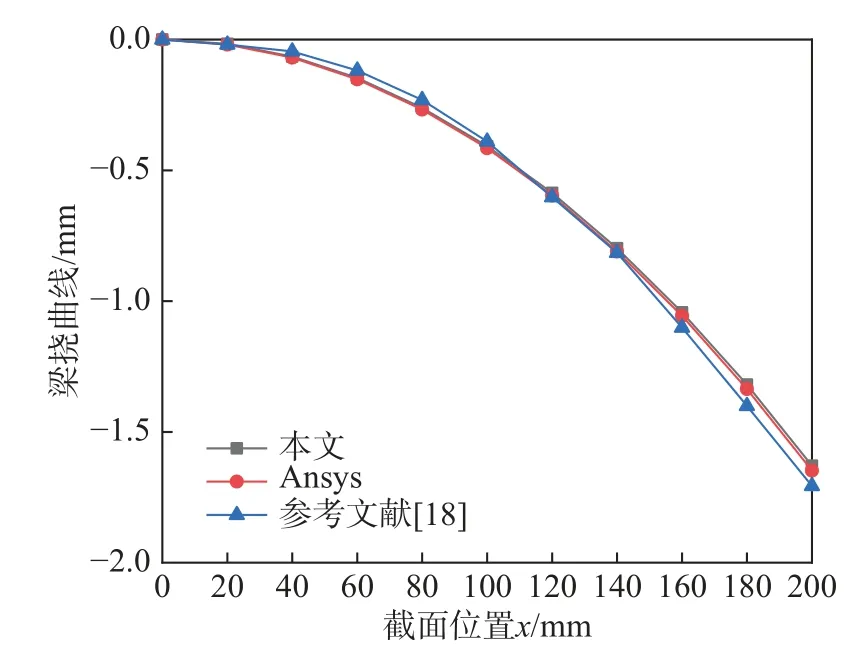
圖5 不同模型給出的溫度荷載作用下梁撓曲線(N=∞)Fig.5 Deflection curvesof beam under temperature load given by different models(N=∞)

3.2 自由振動分析

如圖3所示壓電功能梯度懸臂梁，梁的長度為1 m，功能梯度層厚度hc為0.05 m，由Al 及A l2O3復合而成。上下壓電層厚度hp為0.001m，材料為PZT G1195。本例所用材料參數如下：

為準確計算梁的高階頻率，將其劃分為20個單元。表3為計算所得壓電功能梯度層合梁前五階無量綱化頻率對比。其中Bendine基于Reddy三階剪切變形理論的位移場以及基于Layer-w ise理論描述的線性分布電勢場推導得到兩節點梁單元[11]，并利用此單元求解得到梁在不同梯度分布指數下前五階無量化自由振動頻率。表3為梁前五階自由振動無量綱化頻率λ，其中λ 的表達式為：

表3 壓電功能梯度梁前五階無量綱化自由振動頻率Table3 The first five non-dimensional frequenciesof piezoelectric functionally graded beam

表3中的Ansys解為本文采用3.1節同樣的單元計算所得自由振動頻率。從表中得結果可以看出，使用本文梁單元所算結果與Bendine及Ansys所算結果較為接近，而隨著梯度分布指數增大，梁前五階自由振動頻率均增大。相比較Reddy 梁理論，Shi梁理論基于三維彈性力學及能量等效原理推導得到位移場中的剪切函數，并且以截面的平均轉角為基本場變量可以更好地預測梁的高階頻率，表中梁振動的第五階頻率本文所算結果相比較參考文獻[11]的結果更接近Ansys解。

3.3 壓電功能梯度層合梁最優振動控制

3.3.1非對稱正交鋪設層合梁振動控制

如圖6所示為一個非對稱正交鋪設(0o/90o/0o/90o)層合懸臂梁[20]，其固支端處配置有壓電傳感器及壓電致動器，梁總長度L=100mm，寬度b=10mm。梁由四層等厚度各向同性層組成，其材料為Gr/Ep，總厚度hc=2mm。上下壓電層長度均為Lp=40 mm，其厚度hp=0.2mm。壓電層由PZT G1195組成，其材料參數如3.1節中所示，本例所用彈性層材料參數為：

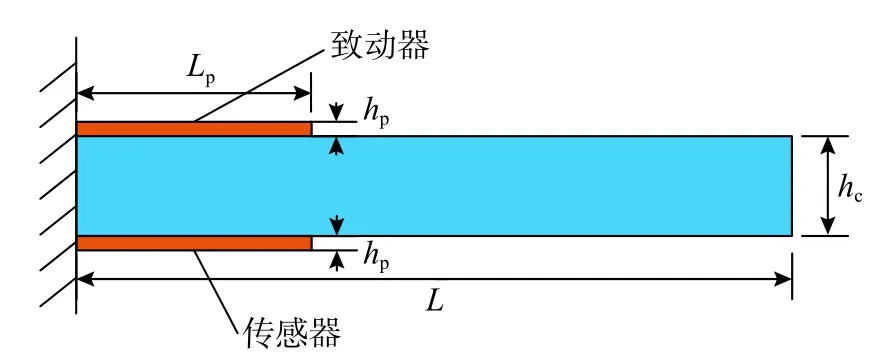
圖6 帶壓電片復合材料懸臂梁幾何示意圖Fig.6 Geometry of cantilever composite beam w ith PZT patches

將梁劃分為5個單元，其中壓電片劃分為2個單元。上層壓電層作為致動器，下層壓電層作為傳感器。在梁端施加大小為1 N 方向向下的沖擊荷載，作用時間為1ms。取結構的前6階模態對其進行控制，設每階模態所對應阻尼比為0.8%。圖7為在沖擊荷載作用下梁端撓度及壓電致動器層控制電壓時間歷程。從兩圖中可以看出，使用LQR 算法所求的最優控制力可有效抑制梁的振動。參考文獻[20]采用3.1節中YASIN 等[14]所提出壓電功能梯度梁單元，此梁單元有一個內部的電學自由度，并且在壓電層表面附加等電勢條件。另外考慮到測量噪聲及觀測噪聲的影響設計了系統的狀態觀測器，采用LQR 算法中性能泛函為輸出變量及控制變量的二次型加權線性組合的輸出調節器求解最優控制力。為與參考文獻[20]比較，本文同樣采用輸出調節器并設計了狀態觀測器求解最優控制力。性能指標中輸出變量的權值Q=50I，而輸入變量的權值R=I。從圖7中可以看出，使用本文梁單元及YASIN 所給出梁單元計算所得未施加控制時梁自由振動曲線基本一致。由于兩者采用不同電學自由度，采用本文梁單元所求解的致動器層電壓相比較YASIN 梁單元所求電壓差異明顯，且前者更低。而相同權值下施加控制后，兩者梁端撓度振動曲線差異較小。

圖7 沖擊荷載下反對稱正交鋪設梁的梁端撓度及壓電片控制電壓的時間歷程Fig.7 Tip deflection and control voltage time historiesof anti-symmetric cross-ply beam under an impulsive load

3.3.2壓電功能梯度層合梁振動控制

本例將研究性能指標函數中加權矩陣Q以及R的權值大小對結構振動最優控制的影響。仍然采用3.2節中的模型，基于前文所提出的梁單元列式已準確求得梁的自由振動頻率如表3所示。現取結構的前五階頻率對其進行振動控制，將梁劃分為10個單元，上層壓電層作為結構的傳感器，下層壓電層作為致動器。梁中心功能梯度層梯度分布指數N=10。初始時刻在梁自由端處施加向下的大小為200 N 的沖擊荷載，作用時間為0.001 s，通過線性二次型最優控制器求得其最優控制電壓，將控制電壓施加在結構的制動器層上實現對其振動的控制。

圖8及圖9為在各能量項前加權系數取不同值時梁端的振幅曲線以及施加在第一個單元上的平均電壓隨時間的變化曲線。表4為不同加權矩陣取值下系統的控制時間及控制電壓。從圖8、圖9以及表4可以看到，固定R的權重，隨著Q權重的增大，梁的振動衰減更快，而施加在致動器層的電壓更高。而在0.1 s以后在電壓變化圖中此趨勢正好相反，考慮到Q權值大的振幅曲線中振幅已經衰減到一定程度，結構并不需要更大的電壓來控制其振動。相反，固定Q的權重，隨著R的權重增大，控制電壓的幅值越低，振動衰減越慢。

圖8 基于不同Q 取值下LQR 算法的振動控制梁端撓度及控制電壓的時間歷程Fig.8 Tip deflection and control voltage for the optimal vibration control of piezoelectric functionally graded beam using LQR scheme w ith various weighting matrixes Q

圖9 基于不同R取值下LQR 算法的振動控制梁端撓度及控制電壓的時間歷程Fig.9 Tip deflection and control voltage for the optimal vibration control of piezoelectric functionally graded beam using LQR scheme w ith variousweighting matrix R

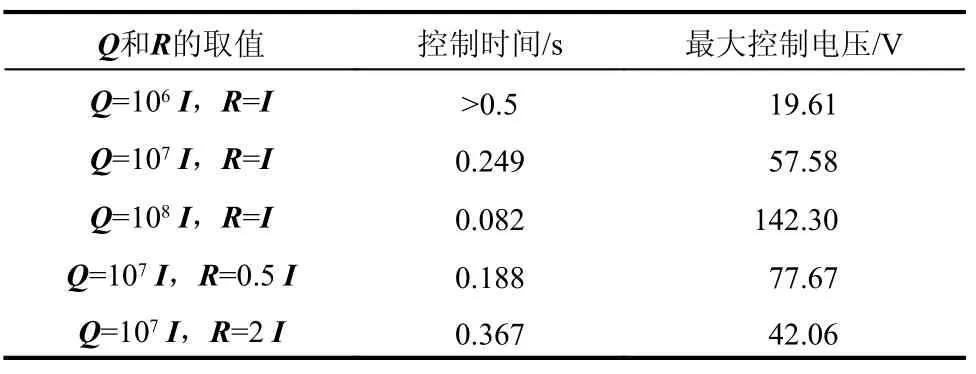
表4 Q、R不同取值下梁振動控制時間及最大控制電壓比較Table 4 The comparison of control time and maximum control voltage w ith different valuesof Q and R

4 結論

本文基于雜交板理論推導了一個C1連續的兩節點壓電功能梯度層合梁單元，其中以SHI改進的三階剪切變形理論表示梁內位移場，以Layer-w ise理論表示梁內壓電層電勢場。基于Ham ilton 變分原理推導得到梁單元的有限元列式，并將此有限元列式用于壓電功能梯度層合梁的靜力分析及動力分析。通過LQR 最優控制算法求得最優控制力實現對壓電功能梯度梁的振動最優控制。數值算例結果表明：

(1)所得壓電功能梯度層合梁單元的位移與應力計算結果與Ansys的二維彈性力學單元計算結果一致。但本文使用的梁單元比二維彈性力學模型所使用的單元少很多，表明本文所給梁單元可以準確且高效地描述壓電功能梯度層合梁的力-電-熱耦合效應。

(2)壓電功能梯度層合梁的頻率分析計算結果顯示，以截面平均轉角為基本場變量的SHI改進三階剪切變形理論給出比其他三階剪切變形梁理論更準確的高階振動頻率。

(3)利用LQR 最優控制算法所得最優控制力可有效抑制結構的振動。二次型性能指標泛函中狀態變量的權重Q越大，梁的振動衰減越快，控制電壓越高。增大輸入變量的權重R，梁的振動衰減越慢，控制電壓越低。