基于模態綜合法和模態疊加法的密集模態結構響應重構

鄒云峰，盧玄東，陽勁松，周 帥，何旭輝

(1.中南大學土木工程學院，湖南，長沙 410075；2.軌道交通工程結構防災減災湖南省重點實驗室，湖南，長沙 410075；3.中南大學交通運輸工程學院，湖南，長沙 410075；4.中國建筑第五工程局有限公司，湖南，長沙 410004)

土木工程結構的性能在其使用過程中會隨著時間的推移而下降，為了監測結構的健康狀況和進行壽命預估，有必要準確獲得結構關鍵區域的系統響應[1-2]。結構動力響應重構在過去十幾年中受到越來越多的關注。然而，鑒于工程結構的幾何復雜性及部件多樣性，某些位置(例如結構交界面、狹縫等)皆不易安裝傳感器，實際中并不總是能在期望的位置進行測量[3-4]。因此，預測關鍵點的動態響應成為進行結構健康監測的重要組成部分[5- 6]。

目前，響應重構方法主要可分兩種：頻域方法和時域方法。在頻域方法中，RIBEIRO等[7]首先提出了傳遞率概念，定義為頻域中已知響應函數和其他未知響應函數之間的傳遞率矩陣，通過傳遞率可以實現結構任意位置的響應重構；DEVRIENDT等[8]提出另一個傳遞率概念，定義為響應譜和單個參考響應譜之間的比值，在響應重構中僅應用于全局傳遞性；LAW 等[9- 11]基于頻響函數將上述位移傳遞率推廣至加速度傳遞率，完成了全模型或子結構上的響應重構。以上的頻域方法使用頻率響應域中的數據，而且通過逆傅里葉變換來將重構的頻域響應轉換回時域，會引入額外的計算成本和數值截斷誤差。在時域方法中，HE等[12-13]提出一種基于經驗模態分解(EMD)的時域響應重構方法，將采集響應分解為由固有模態函數表示的模態響應，然后，利用這些模態響應計算待測位置的模態響應，最后，采用模態疊加法實現時域動態響應重構。為了確保通過EMD得到本征模態函數(IMF)的只包含一個頻率成分，還加入了間歇性準則進行頻率篩選。該方法在計算成本方面非常有效，并且適用于基于不同類型的傳感器測量的動態響應重構，相比于頻域方法有著更高的計算效率。

然而，基于EMD的響應重構方法應用于大型土木結構存在一定困難。一方面，該方法需要獲取整個結構的全局剛度矩陣與質量矩陣，而大型土木工程結構通常維數較大，在提取剛度矩陣、質量矩陣時需要大量的計算資源和時間；另一方面，帶間歇性準則的EMD方法不能有效地分離密集模態，從而難以實現存在密集模態結構的響應的重構。

針對以上兩種限制，本文提出一種基于模態綜合法和改進模態疊加法的響應重構方法。該方法結合了模態綜合法[14-16]，將結構全模型經過兩次坐標變換縮聚為自由度更少的超單元模型，并通過在超單元模型上計算的模態振型進行動態響應重構；當存在密集模態時，在超單元模型的基礎上，將結構模態分為密集模態和剩余模態[17-18]，其中剩余模態的重構通過基于EMD的重構方法實現，密集模態的重構響應可由模態振型和剩余模態計算得到，最后通過模態響應疊加獲得待測位置響應。

1 理論推導

1.1 子結構模態綜合法

對于一般的土木工程結構而言，可以根據結構的連接特性、實際工程需要等因素劃分成多個子結構。在有限元基礎上，子結構的動力學運動方程可表示為：

式中：上標s表示第s個子結構；Ms、Cs及Ks分別為子結構的有限元模型的質量矩陣、阻尼矩陣及剛度矩陣；Xs(t) 、分別為自由度位移、速度及加速度；fs(t)為子結構所受外力，gs(t)為子結構的界面力。

根據Craig-Bampton 提出的固定界面模態綜合法，式(1)中的自由度可分成內部組“i”和邊界組“j”，其中，內部組中的自由度不與任何子結構共有，邊界組必須包含實際的“邊界”，即子結構與子結構之間共有的自由度，也可以將子結構內部任意自由度歸到邊界組中。將式(1)中的各矩陣的元素按如下形式重新排序：

提取第s個子結構的模態轉換矩陣 Φs，該矩陣由兩個子集組成，即固定界面選取的主模態集和全部界面坐標的約束模態集：

將式(4)代入式(1)，并令Xs=Φsqs，其中qs表示第s個子結構的模態坐標向量，則式(1)可表示為：

根據式(3)，模態坐標q和原坐標X之間的關系可具體表示為：

即經過第一次坐標變換后，邊界組中自由度的模態坐標下的響應與對應的原結構響應相等。

各子結構進行第一次坐標變換之后，整合所有子結構，則整個模型的動力學運動方程可表示為：

其中：

由于各個子結構之間存在共有自由度，因此模態坐標q中的元素不是獨立的，需要經過第二次坐標變換消除非獨立坐標。結合布爾矩陣L可將各子結構耦合成全模型的超單元模型，當各子結構耦合為一個超單元模型之后，界面力為零，即LTg(t)=0，令q=Lp，其中p表示獨立坐標，并代入式(8)，則整個超單元模型的動力學運動方程可表示為：

式(10)中各矩陣可表示為：

第二次坐標變換只消除耦合模型中的非獨立坐標或改變各個坐標的排列順序，并不會改變元素大小，因此根據式(7)，可以得到以下關系：

基于超單元模型的響應重構需要求解模型的超單元模態振型矩陣，如下所示：

1.2 基于改進模態疊加法的子結構重構理論

假設結構第w階和第v階模態為密集模態，下標a和r分別表示密集模態和剩余模態，下標m和u分別表示響應采集處自由度和待測響應自由度。將響應采集自由度和待測自由度分別置于邊界組中，結合式(11)，超單元基礎上的已知響應集與未知響應集如下所示：

式中：Da1(t),Da2(t)···Daa(t)為模態坐標中的密集模態響應；Dr1(t),Dr2(t)···Drr(t)為模態坐標中的剩余模態響應。由式(17)得模態坐標下的密集模態響應為：

式中：上標+表示矩陣的廣義逆。在這里，已知響應的數目應不小于密集模態的總數。結合式(16)和式(18)，將各個模態組分進行疊加可得未知響應向量：

定義如下四個矩陣：

式中：下標b表示第b自由度(響應采集量中的某個響應自由度)；下標r1、r2…rr表示剩余的r個模態；為第b個自由度的剩余模態響應。式(20)可表示為如下形式：

若結構的模態中存在密集模態，在響應的傅里葉譜上可能難以辨別其中某一組密集模態具體包含了哪幾階模態，這時候可以選擇將該組密集模態可能包含的模態都視為密集模態來計算，并根據式(25)重構。該重構方法適用于應力、應變、位移、加速度等動力響應的重構。

2 數值模擬算例

通過輸電塔案例驗證所提出的響應重構方法對大型結構的適用性。輸電塔的有限元模型由ANSYSAPDL建立，如圖1所示，其中單元類型為beam188，共有3123個單元，2764個節點，16 584個自由度，結構底部通過四個固定約束與地面連結。模型建成后，在ANSYS內提取剛度矩陣和質量矩陣并導入MATLAB中，結構響應的模擬和重構都在MATLAB中實現。

圖1 輸電塔模型Fig.1 The model of power transm ission tower

為了獲取結構響應，假設在結構中設置了6個響應采集點，如圖1所示，這些采集點位于離地高度較小的位置，也是在實際中便于安裝傳感器的位置。此外，響應重構點Loc.R 的位置也在圖1中標出。將由15階低通巴特沃斯濾波器過濾的白噪聲模擬的隨機荷載施加于輸電塔的多個節點上，每階模態阻尼設為1%，采樣頻率為1 kHz。在超單元模型上根據式(13)計算模態頻率矩陣，得出前11階結構固有頻率分別為8.14 Hz、17.89 Hz、36.31 Hz、38.55 Hz、39.38 Hz、45.29 Hz、73.52 Hz、86.41 Hz、87.32 Hz、87.78 Hz 和90.40 Hz，圖2是響應采集位置Loc.K 的響應傅里葉譜。通過對六個響應采集點的響應傅里葉譜進行分析，第11階模態(頻率為90.4Hz)及其后的模態并沒有明顯的幅值，為了簡化計算，在本案例中僅考慮對響應有較大貢獻的前10階模態。根據超單元模型計算的固有頻率值，將第1階、2階、6階、7階模態視為單階剩余模態；第3階～5階模態和第8階～10階模態內的頻率間隔很小，很難使用傳統的EMD方法對其進行準確的分離，因此將第3階～5階模態和第8階～10階模態歸入密集模態組。

圖2 Loc.K 的響應傅里葉譜Fig.2 Spectrum of the response of Loc.K

按照基于模態綜合法和模態疊加法的密集模態結構響應重構方法計算Loc.R 的動力響應，重構的基本流程如圖3所示。圖4所示為子結構劃分示意圖，上半部分結構為子結構1，下半部分結構為子結構2，每個子結構縮聚后均保留20個主模態。本算例中超單元模型的邊界組自由度包括子結構1和子結構2的界面自由度，以及輸電塔底部多個自由度(包含所有響應采集點)和重構點對應的自由度，壓縮后的超單元模型共包含148個自由度，在超單元模型上的重構過程如下：

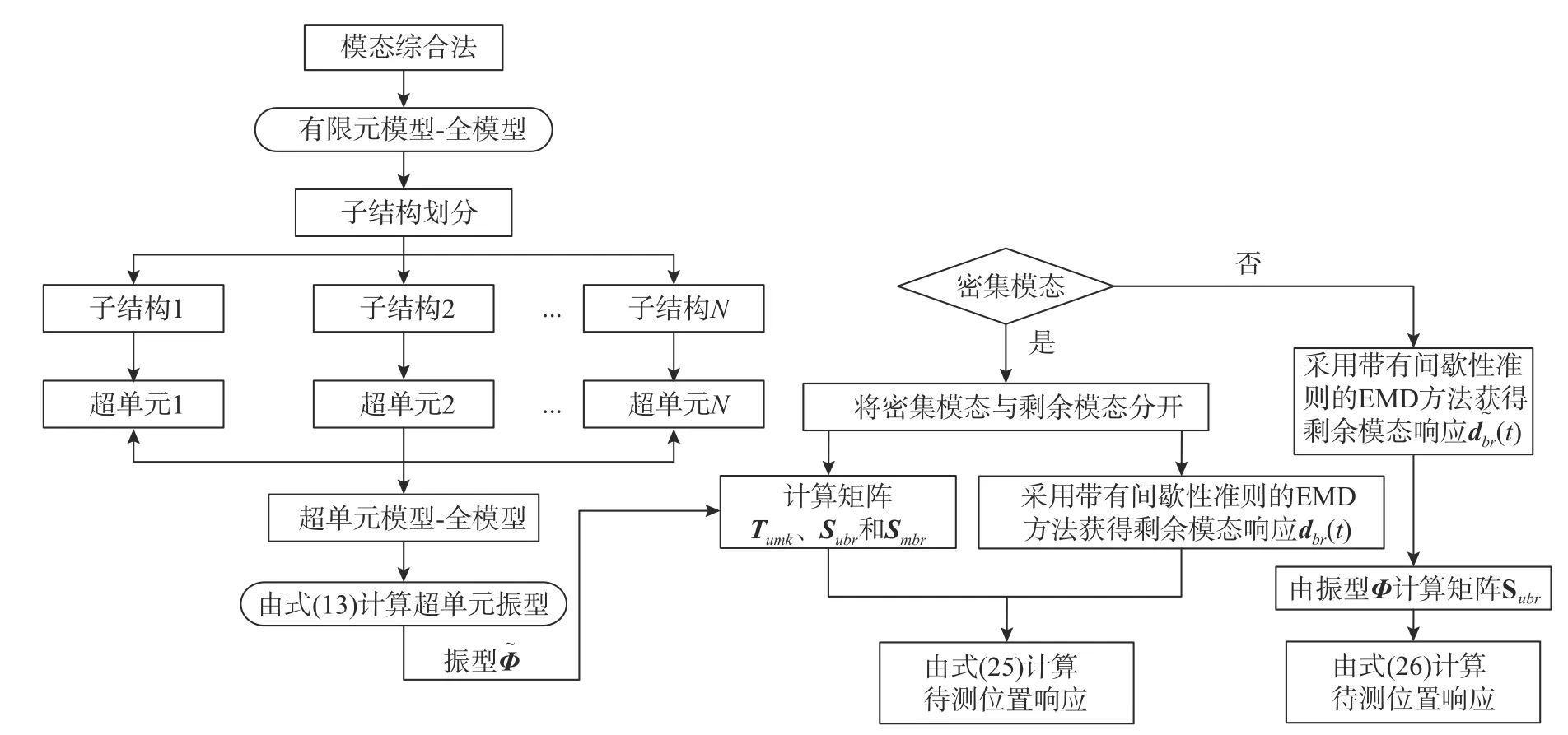
圖3 重構流程圖Fig.3 Flow chart of the response reconstruction method

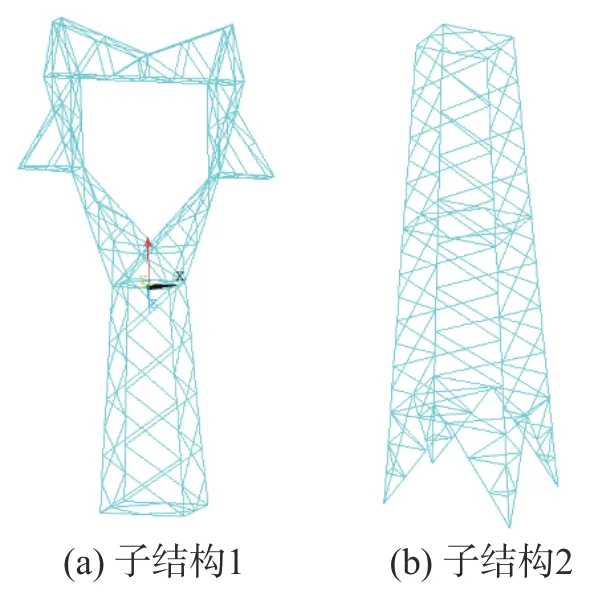
圖4 子結構劃分示意Fig.4 Division of two substructure

1)由式(13)計算超單元模型的振型 Φ～；

2)根據式(21)～式(23)計算Tuam、Subr和Smbr。在該案例中，對應于下標m的響應采集位置包括Loc.K、Loc.L、Loc.M、Loc.N、Loc.O、Loc.P；對應于下標m的響應重構位置僅有Loc.R；對應于下標a的密集模態包括第3階、4階、5階、8階、9階、10 階模態；對應于下標r的剩余模態包括第1階、2階、6階、7階模態；

3)使用EMD方法提取Loc.K 的剩余模態響應，由此構建矩陣式(24)中的矩陣EMD方法的性能取決于帶通濾波器分離不同模式的能力。表1 給出了提取剩余模態響應的帶通濾波器的頻率范圍；

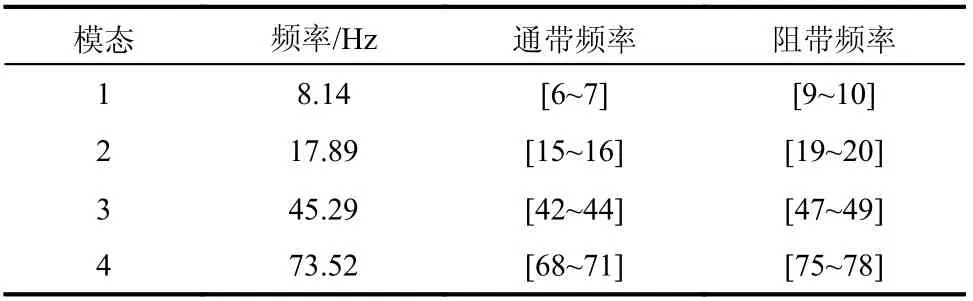
表1 使用EMD方法的每個帶通濾波器頻率范圍Table1 Frequency ranges for each band-pass filter using the EMD method

4)根據式(25)重構Loc.R 的響應。

重構的理論值與重構值對比如圖5所示。為了定量評價重構的精度，定義一種相對誤差(RE)用以反映重構值偏離理論值的程度，以及平均絕對誤差(MAE)用以評價重構值的平均偏移量，如下所示：

式中：n為時間序列長度；p(t)為 重構值；為理論值。圖5中重構值和理論值的RE和MAE分別為1.129%和0.103%，重構精度較高。

圖5 理論響應與重構響應Fig.5 Theoretical response and reconstructed response

接下來使用傳統的EMD 方法進行重構，即按照式(26)的重構方法獲取待測位置的響應。選取Loc.K 的響應重構Loc.R的響應，表2給出了每個帶通濾波器的頻率范圍。Loc.R 的重構響應和理論響應對比如圖6所示，RE和MAE分別為67.254%和0.815%，重構誤差很大，說明在該案例中傳統的EMD方法不能準確實現待測位置響應的重構。

表2 使用傳統EMD 方法的每個帶通濾波器頻率范圍Table2 Frequency ranges for each band-pass filter using traditional EMDmethod

圖6 理論響應與重構響應(使用傳統的EMD方法)Fig.6 Theoretical response and reconstructed response(using traditional EMDmethod)

此外，大型結構的參數矩陣(剛度矩陣和質量矩陣)存在著大量的數據冗余，即包含很多零元素，在重構全過程中會耗費大量時間和內存。表3給出了原模型和子結構的數據量對比，可以看出，劃分為兩個子結構之后，參與運算的數據大約減少一半，有效緩解了計算機內存不足和計算時間冗長的問題。

表3 原模型和超單元模型的運算數據量Table3 Calculation data of original model and super-element model

2.1 主模態數量的影響

根據式(3)可知，在坐標變換過程中人為選擇了保留的主模態數量，該數目通常遠小于原結構的自由度數量，以此達到模型縮聚的效果。顯然，不同的主模態數量會改變最終超單元模型的振型計算值，從而影響重構結果。為了驗證主模態數量對所提出的響應重構方法的影響，對比每個子結構選取的主模態數量分別為2、4、6、10和20時的重構結果。待測位置響應的重構值和理論值對比如圖7所示，此外還給出了各主模態數量下的重構精度，如表4所示。

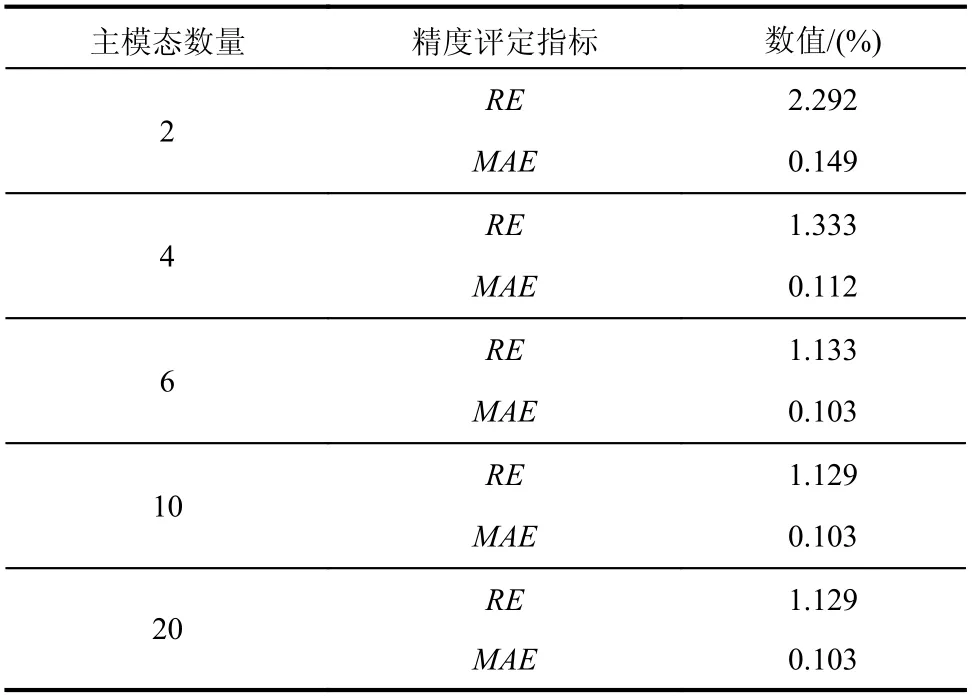
表4 不同主模態數量下的重構精度Table4 Reconstruction accuracy under different number of main modes

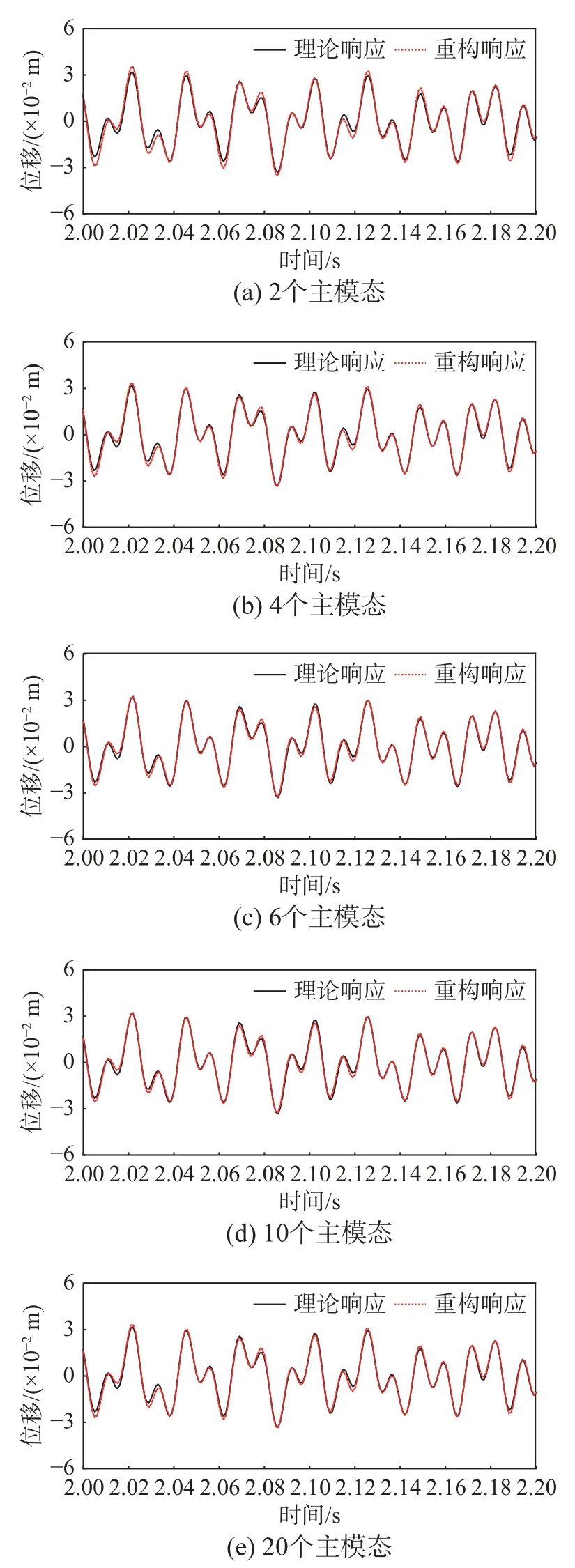
圖7 不同主模態數量下的理論值與重構值Fig.7 Theoretical value and reconstructed value under different number of main modes

2.2 子結構劃分方式的影響

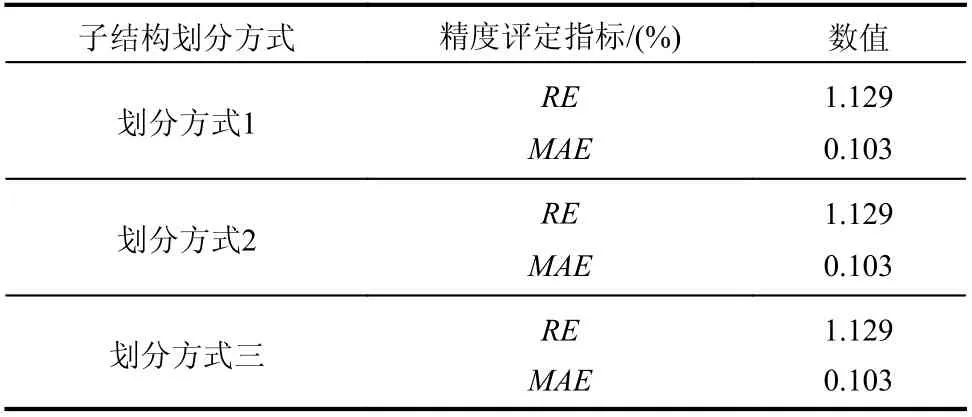
表5 不同子結構劃分方式下的重構精度Table5 Reconstruction accuracy under different different substructure division

圖8 子結構劃分方式1Fig.8 Substructure division 1

圖10 子結構劃分方式3Fig.10 Substructure division 3

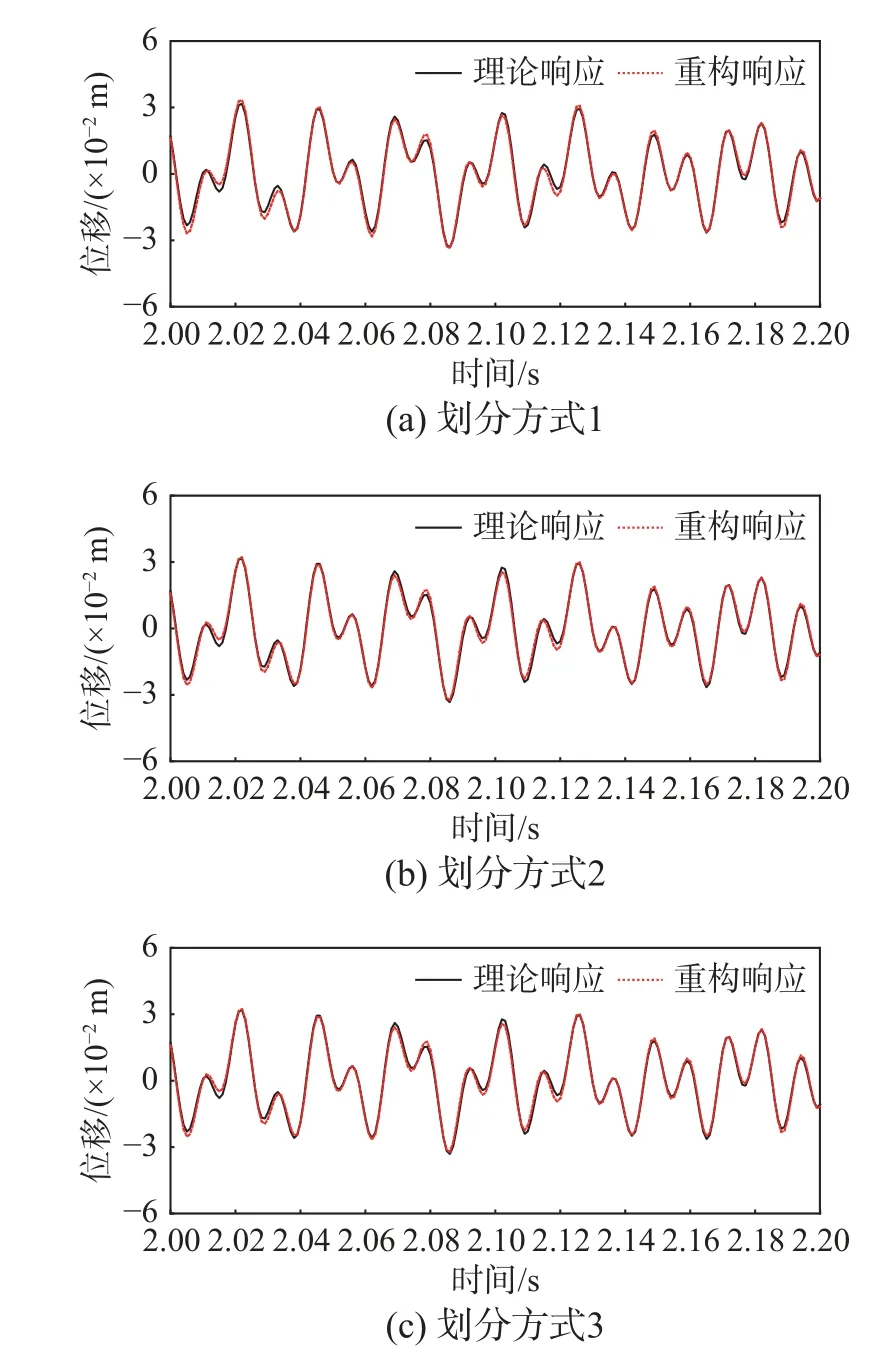
圖11 不同子結構劃分方式下的理論值與重構值Fig.11 Theoreticalvalue and reconstructed value under different substructure division

圖9 子結構劃分方式2 Fig.9 Substructure division 2

相對于直接提取原模型的參數矩陣而言，通過分別提取各子結構的參數矩陣再進行耦合的方法，在保證重構精度的前提下，可以減少運算的數據量。表6給出了不同子結構劃分下的重構運算數據量對比，可以看出，一定范圍內子結構數量越多，運算數據總量越少，對計算效率的提升也越明顯。但是隨著子結構數量的增大，將需要更多人力設置相應的界面耦合。因此在實際中應綜合考慮計算效率和人力投入來劃分合適的子結構數量。

表6 不同子結構劃分的重構運算數據量。Table 6 Calculation data of reconstruction under differentsubstructure division

2.3 噪聲等級的影響

現實中響應采集不可避免地存在噪聲，為了所提出的響應重構方法在測量噪聲環境下的適用性，研究在同一組外部激勵下，不同等級的噪聲(5%、10%、15%和20%)對重構的影響。測量噪聲用高斯脈沖過程來表示，其均方根設置為應變最大均方根的百分比，這里使用噪聲等級來表征噪聲程度，即添加的噪聲是響應最大均方根值等同于噪聲等級的高斯過程。重構結果如圖12和表7所示，可以看出，重構精度會受到噪聲的影響，隨著噪聲的增大而降低，而且重構響應上的鋸齒也趨于明顯。

表7 不同噪聲等級下的重構精度Table7 Reconstruction accuracy under different noise level

圖12 不同噪聲等級下的理論值與重構值Fig.12 Theoreticalvalue and reconstructed value under different noise level

EMD方法本身有著一定的降噪性能，而在本文所提出的重構方法中，僅用EMD提取剩余的單頻模態響應，對于密集模態響應則通過已知響應、提取的剩余模態響應和振型矩陣外推至響應重構點，這樣一來，已知響應中的噪聲將被保留至響應重構點，對重構結果產生影響。因此，對于密集模態成分主導的結構響應，該方法難以在高噪聲的情況下重構出準確的結果。對于該案例而言，在不大于15%的噪聲下進行重構能得到較為準確的結果。

2.4 阻尼的影響

在前文的論述中，該案例采用1%模態阻尼以模擬阻尼效應，而實際工程結構可能存在更高的阻尼，因此接下來討論不同的阻尼對重構結果的影響。對于同一組外部激勵，考慮三種模態阻尼(2%、4%和6%)，不同阻尼下的重構結果如圖13和表8所示所示。

圖13 不同阻尼下的理論值與重構值Fig.13 Theoreticalvalue and reconstructed value under different damp

表8 不同阻尼下的重構精度Table8 Reconstruction accuracy under different damp

從重構結果可以看出，RE隨著阻尼的增大而明顯增大，說明在高阻尼下重構精度相對較低。本文所提出的方法將結構響應頻率的模態振型和模態響應一一對應實現重構，其基本思想是：結構響應可分解為多個模態響應的疊加，每個模態響應對應著一個固有頻率。圖14 給出了不同阻尼下的Loc.K 的響應傅里葉譜，可以看出，隨著阻尼的增高，各個模態的能量趨于分散，難以與單一頻率相對應，因此高阻尼下重構精度差。對于該輸電塔結構而言，應保證重構在模態阻尼不大于4%下的情況下進行。

圖14 不同阻尼下Loc.K 的響應傅里葉譜Fig.14 Spectrum of the response of Loc.K under different damp

3 結論

本文提出了一種基于模態綜合法和模態疊加法的密集模態結構響應重構方法，以輸電塔結構為例開展了響應重構數值計算，探討了主模態數量、子結構劃分方式、噪聲等級以及阻尼對重構結果的影響，得到主要結論如下：

(1)該方法結合了模態綜合法，通過模型縮聚，參與計算的剛度和質量矩陣數據量大大減少，由此改善了計算機內存不足的問題，從而更加適用于大型結構。

(2)鑒于EMD法難以分離密集模態，本文提出將密集模態視作一個整體，并由剩余模態替代的方法，改善了傳統EMD方法不能分離頻率間隔較小的模態而無法準確重構未知響應這一不足，且適用于于應力、應變、位移、加速度等各種動力響應的重構。

(3)以輸電塔為例的數值計算表明，當主模態數量很小時，重構精度較差，隨著主模態數量增加，重構精度趨于穩定，可以考慮保留兩倍于結構響應貢獻較大的模態階數的主模態數量；子結構劃分方式對該重構精度的影響極小，應綜合考慮計算效率和人力投入劃分適當的子結構數量。

(4)測量噪聲等級越高，重構精度越低，對于密集模態主導且噪聲等級較高的情況，難以得到理想的重構結果，作者在今后的研究中也將尋求適合的濾波降噪方法應用于該重構方法；結構阻尼對重構有較大影響，這是因為高阻尼下各個模態的能量趨于分散，難以和單一頻率相對應，應保證案例的輸電塔結構的重構在模態阻尼不大于4%下的情況下進行。