基于非局部Biot 理論的循環荷載下飽和土地基動力特性研究

丁海濱，管凌霄，童立紅，徐長節,3，顏建偉

(1.華東交通大學軌道交通基礎設施性能監測與保障國家重點實驗室，江西，南昌 330013；2.江西省地下空間技術開發工程研究中心，江西，南昌 330013；3.華東交通大學江西省巖土工程基礎設施安全與控制重點實驗室，江西，南昌 330013)

探究循環動荷載下飽和土地基的動力響應及固結沉降對實際工程具有重要意義，如廠房機械振動對地基的影響，列車荷載下飽和地基動力特性及軟土地區地基加固[1]等。飽和孔隙介質的動力控制方程最早是由BIOT[2- 3]提出，該方程能夠較準確地反映飽和土的動力特性。之后，許多學者[4-5]通過室內動力實驗驗證了Biot 理論的正確性。Biot理論也因其形式簡單且其模型參數易通過試驗獲得，而在實際工程得到了廣泛的應用。Biot 動力控制方程的原始形式中的變量為u(土骨架位移)和w(流體相對土骨架位移)，即u-w格式控制方程。后續學者們根據所研究問題的不同，將原始的控制方程變換為u-p和u-w-p等格式的控制方程[6-7]。

由于基于Biot 理論的二維或者三維固結問題的解析解難以獲得，目前學者們所求得的解析解都是對所研究的問題進行簡化后獲得的，如：簡化為軸對稱問題[8-9]，或者將該問題簡化為一維問題，求得其解析解[10-12]。簡化所得到的解析解與實際情況存在一定的差異，為此，學者大多采用數值方法求解Biot 理論控制方程。PREVOST[13]采用有限元法和隱式積分算法，研究了波在飽和土兩相介質中的傳播問題。CARTER 等[14]采用有限元數值方法求解了彈塑性地基的固結問題。SIMON等[15]采用有限元法研究了u-w，u-w-p及u-p三種形式的控制方程在飽和孔隙介質的復雜邊值中的應用。FERRONATO等[16]提出了三維混合有限元方程，求解了Biot 固結方程，以減輕數值計算引起的孔隙水壓不穩定問題。MENENDEZ等[17]采用有限元法求解了不可壓縮流體和滲透系數變化的固結模型，分析了飽和土介質的非線性固結問題。基于Arbitrary Lagrangian-Eulerian 法和摩爾庫倫(MC)及修正劍橋本構模型(MCC)，SABETAMAL等[18]采用Generalized-α 積分法對u-p耦合控制方程時間進行離散，求解了荷載作用下飽和孔隙介質的大變形問題。基于Biot 固結理論，WU 等[19-20]采用數值流變模型建立了飽和土動力固結的有限元方程，編制了有限元計算程序，分析了外荷載作用下低滲透性飽和黏土邊坡的動力固結問題。NAVAS等[21-23]基于u-w格式的控制方程，采用局部最大熵原理(LME)構建無網格法形函數，研究了飽和土地基的固結問題。NAZEM等[24]提出最大熵無網格法，用于研究飽和土介質的固結問題，結果顯示所提出的模型可給出固結沉降的穩定的解。TORABI等[25]提出了一種求解固結方程的穩定時間積分算法。

然而，以上針對飽和孔隙介質動力固結的研究都是基于經典Biot 理論，雖然Biot 理論在工程中得到了廣泛的應用，其假設飽和土中的波長遠大于孔隙尺寸，但在高頻情況下該假設已不再成立[26]。為此，TONG 等[27]通過引入了非局部參數考慮了孔隙尺寸效應的影響，提出了非局部Biot理論。隨后，利用非局部Biot 理論，TONG等[28]研究了飽和土介質中Rayleigh 波傳播特性；XU等[29]，DING 等[30]及徐長節等[31]研究飽和土介質中圓形襯砌的動力響應問題；TONG 等[32- 33]研究移動荷載下飽和土地基的動力響應問題。

由以上分析可知，高頻下，孔隙尺寸效應對結構動力特性的影響顯著，為此，本文基于TONG等[27]所構建的u-w形式的非局部Biot 理論，采用有限單元法，結合虛位移原理及Newmark 積分法，得到了非局部Biot 理論的有限元離散方程，編制對應的有限元計算程序，分析孔隙尺寸效應對循環動荷載作用下飽和土地基動力特性的影響。本文得到了非局部Biot 理論的控制方程數值解，使其能用于解決復雜的工程問題，以期為實際工程中循環動荷載下飽和土地基動力響應及固結沉降問題提供參考。

1 非局部Biot 控制方程的有限元空間離散

1.1 非局部Biot 理論控制方程

采用有限元求解一個系統，首先需建立并求解該系統的線性方程組，稱之為有限元方程。有多種方法可用于求解有限元方程，如加權參數法、虛位移法及變分原理等。本章采用虛位移法獲得系統的有限元方程。非局部Biot 理論控制方程式為[27]：

式中：u、w分別為土骨架位移和流體相對于土骨架位移； α =1-Kb/Ks；M為Biot 參數； ?2為Laplace算子； σ′為總Cauchy 應力； ρf為孔隙流體的體積密度， ρ =(1-n0)ρs+n0ρf，n0為初始孔隙比， ρs為土顆粒密度； ?0為非局部參數，該參數可由室內波速試驗測定，其包含孔隙尺寸效應及由于波動所引起的孔隙動力效應兩部分[27]，主要反映土顆粒之間相互作用的影響范圍；為曲度因子；η為流體粘滯系數；κ為滲透系數；F(ζ)為粘性修正系數，ω為 圓頻率，；a為孔隙半徑，圓孔狀孔隙時：裂縫狀孔隙時：ξ 為 彎曲因子；ber 和 bei分別為第一類零階開爾文函數的實部和虛部。

1.2 邊界條件

設有限元求解域為Ω，求解域的邊界為，則式(1)應滿足邊界條件：

強制邊界條件：

自然邊界條件：

且各邊界條件應滿足如下關系：

1.3 空間離散

本章采用虛位移原理得到式(1)的空間離散方程，假設 δu為 土骨架的虛位移矢量， δw為流體相對固體虛位移矢量，則式(1)可表示為：

對變量場u和w引入同階等參數單元差值函數：

式中：ue(x,t)和we(x,t)分別為單元土骨架和孔隙流體的位移場；x為空間坐標矢量；t為時間；分別為土骨架和孔隙流體節點位移矢量；Ni(x)為單元形函數；ne為單元節點數目；I為單位矩陣。和僅表示矩陣的乘積運算。

將式(7)中第一式和第二式分別代入式(5)和式(6)，采用Galerkin 法，可將式(5)和式(6)寫成等效積分弱形式[34]：

其中：

2 非局部Biot 理論控制方程的時間離散

式(8)為非局部Biot 理論離散后的控制方程，本文考慮線彈性材料，因此則式(8)簡化為：

為方便后續推導，將(Kss+K′ss)合并為一項，并令為其中彈性矩陣變為，，則式(9)可簡化為：

為編程方便將式(10)寫為：

為求解式(11)，將時域劃分為時間間隔為Δt的小區間， Δt應足夠小，以保證計算的收斂性和精度。由Newmark 積分可知，假設當前時間為n+1，并假設前一時刻n的位移、速度和加速度已知。則n+1時刻的位移、速度和加速度可表示為：

式(17)即為所求的離散方程，β1、β2為Newmark-積分常數，為保證計算穩定，應該滿足β2≥β1≥0.5。本文計算所選取的計算參數值為 β1=0.6和β2=0.605，以引入一定的數值阻尼提高計算的穩定性及收斂性[35]。

3 循環荷載下飽和土動力固結分析

3.1 模型驗證

為驗證所編寫u-w形式的非局部Biot 理論有限元程序的正確性，利用該程序分析飽和土一維固結問題，并將其與Terzaghi 一維固結解析解結果進行對比。為此，假設一個深度為H0=10.0m，寬度為1.0m 的一維固結模型(模型深度遠大于寬度)，模型上邊界設置為排水邊界，頂部施加P0=100 kPa 的均布荷載，底部及兩側為不透水邊界，計算模型及荷載形式如圖1所示。為采用本計算程序模擬上述一維情況，將上述土柱采用4×40個4節點矩形單元離散，并固定所有節點的土骨架及孔隙流體相對土骨架的水平自由度(x方向)。為模擬土柱底部及兩側的不排水情況，將模型底部和兩側節點分別設置為wz=0及wx=0；頂部為排水邊界，即wz所對應的自然邊界條件；頂部外荷載P0全部施加到土骨架豎向(uz方向)自由度上。同時本文理論中的非局部參數τ=0.0 mm，以將非局部Biot 理論退化至經典Biot 理論控制方程。飽和土計算參數按JEREM IC等[36]論文選取，Terzaghi一維固結中假設了土顆粒及孔隙水壓力不可壓縮，因此將土顆粒及孔隙水的體積模量取一個大值，如表1所示。

圖1 一維固結土柱及荷載形式Fig.1 One-dimension consolidation column and loading condition

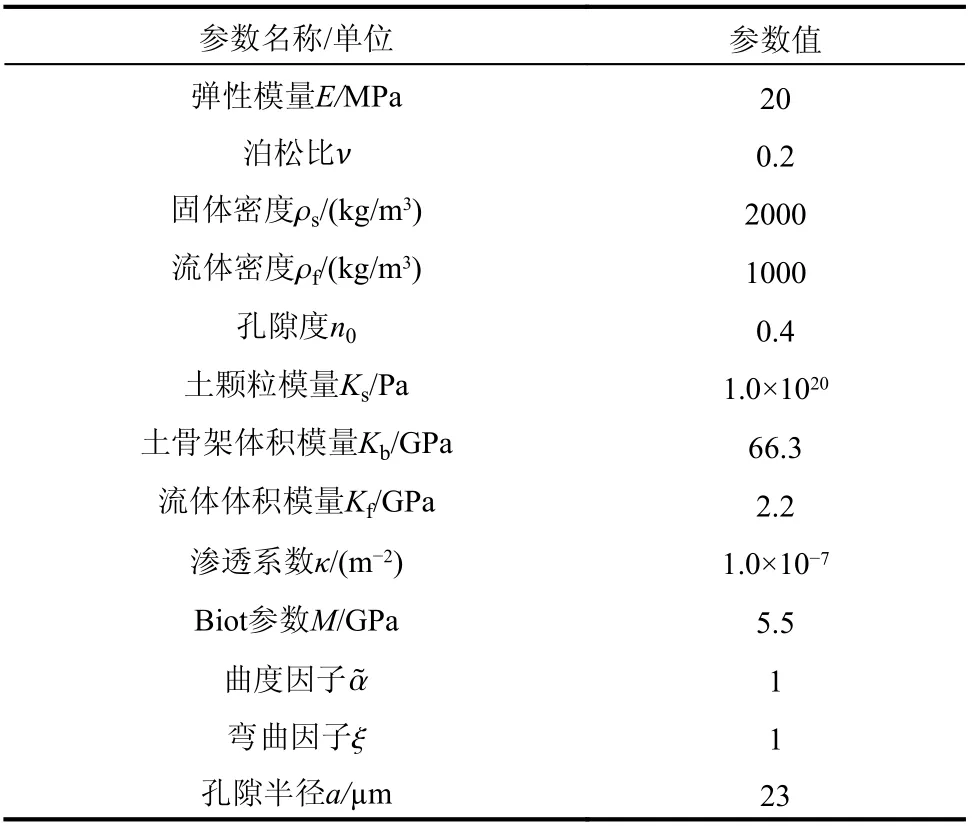
表1 飽和土體參數Table1 parametersof saturated soil

圖2為荷載作用下飽和土土柱一維固結的數值解與解析解的對比曲線，圖中橫坐標為無量綱超靜孔壓p/p0，縱坐標為無量綱深度h/h0。如前所述，Newmark 積分參數取為 β1=0.6 和 β2=0.605，即引入一定的數值阻尼以消除由于外荷載的突然施加而導致的數值波動。由圖2可知，本文所編制程序的計算結果與Terzaghi 解析解結果吻合的很好，由此說明了本文所編制的u-w格式的飽和土體動力固結分析程序的正確性。

圖2 靜載下一維飽和土柱超靜孔壓的數值解與解析解對比Fig.2 Comparing the numerical solution and analytical resultsof the excess pore-pressure for one-dimension saturated column under static load

由于Biot 控制方程的復雜性，目前仍未有二維及三維問題飽和土動力響應問題的解析解，因此為進一步驗證本文所編制u-w格式飽和土控制方程的正確性，將本文的飽和土雙相介質退化為單相介質(通過固定孔隙流體相對固體位移自由度wi，同時取Biot 參數α =M=0)，并與已有數值結果對比[37]。為此，建立高10m，寬100m 的平面應變地基模型，該模型左上角表面1m 范圍內施加均布荷載，均布荷載在時間T內成三角形變化，如圖3所示。退化后土體參數E=100 MPa，ν=0.3 及 ρ=2000 kg/m3，荷載持續時間為T=0.16 s。模型左邊為自由邊界，底面為固定邊界條件，計算結果分析了地基右邊固定及右邊自由兩種工況下地基頂部中點A處的位移，并將計算結果與JU 和WANG[37]的論文結果對比。

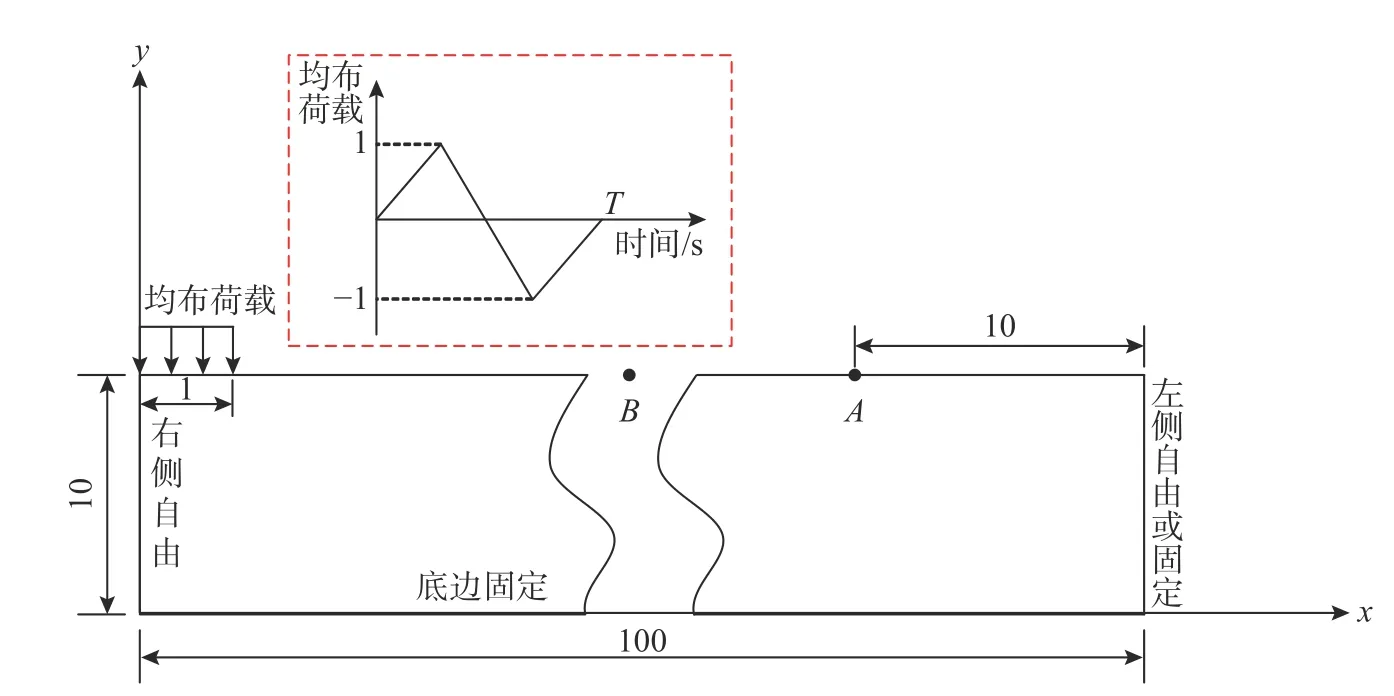
圖3 平面應變地基模型示意圖/m Fig.3 Foundation model of plane strain

圖4為模型右邊界固定及自由情況下本文計算結果與JU 和WANG[37]的計算結果對比曲線，由圖可知，右端固定和自由時，本文結果與JU 和WANG[37]的計算結果均吻合的很好，由此驗證本文計算程序的正確性。

圖4 模型頂面中點A水平位移ux 時程曲線Fig.4 The time-history curve of horizontal displacement ux of point A at the top surface of themodel

3.2 算例分析

為研究孔隙尺寸效應對循環動荷載下飽和土動力響應的影響，本節將選取幾個典型的實例進行參數分析，以研究孔隙尺寸效應對飽和土地基的動力固結及動力響應的影響。具體如下：

3.2.1循環荷載下一維動力固結

循環荷載下飽和土的一維固結計算模型尺寸如圖1所示，但模型頂部作用正弦荷載P=P0sin(ωt)，其中：P0=100 kPa為 正弦荷載幅值；ω=2πf為圓頻率；f=1/T為正弦荷載頻率；T為正弦荷載周期；位移觀測點位于土柱中心，孔隙水壓力觀測點位于模型底面，數值積分采用Newmark 積分，時間間隔 Δt應隨所施加荷載頻率的變化而變化，如：頻率較小時，時間間隔 Δt可選取較大值，而頻率較大時選取的時間間隔 Δt應較小(本文計算時滿足Δt≤T/8，即1/4荷載區域內應有包含兩個時間積分點，以保證計算的精度)；模型左右邊界約束固體顆粒及流體的法向位移，底部為固定邊界和不透水邊界條件；飽和土的物理力學參數見表2中的材料1。

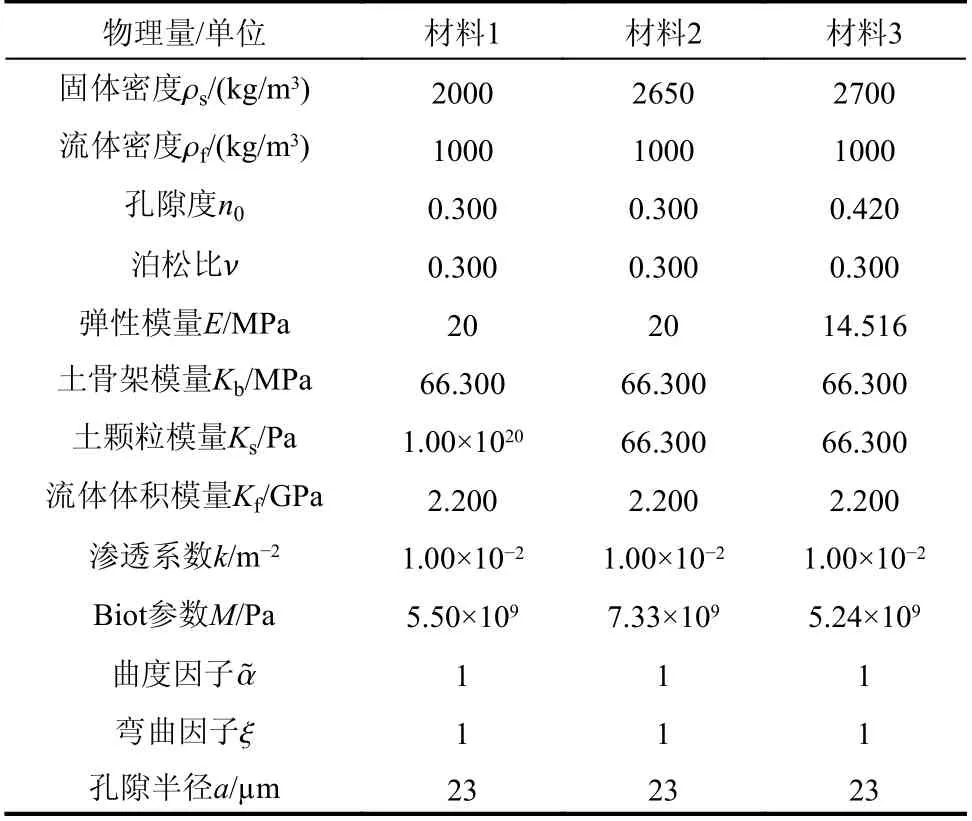
表2 飽和土物理力學參數Table2 physical and mechanical parametersof saturated soil

圖5為荷載頻率不同時，觀測點O的位移時域響應，表征孔隙尺寸效應的非局部參數取值分別為0.00 m、0.04m 和0.08 m。由圖可知，荷載頻率為500Hz 時，觀測點O的位移響應隨非局部參數的增加，變化不大。而由圖5(b)～圖5(d)可以看出，隨非局部參數的增加，位移響應的峰值向后移動，即飽和土中波的相位差發生了變化。這是由于頻率較小時，循環荷載在飽和土內產生的波的波長較長，此時可以認為飽和土中的波長遠大于飽和土介質的孔隙尺寸，由此導致孔隙尺寸效應的影響并不明顯。而隨著荷載振動頻率的增加，循環荷載在飽和土中產生的波的頻率增加，此時，飽和土中的波長接近甚至小于飽和土介質的孔隙尺寸，由TONG 等[27]研究結果可知，考慮孔隙尺寸效應時，隨波頻率的增加，飽和土介質的波速減小，由此導致隨非局部參數的增加，觀測點O的位移響應向后移動。

圖6為不同荷載頻率時，觀測點B的孔隙水壓力隨時間變化曲線。由圖可知，荷載頻率較低時，非局部Biot 理論的計算結果與經典Biot 理論計算結果幾乎一致，而頻率較高時，此時，隨非局部參數的增加，改變了飽和土介質中波速的相位差，由此導致孔隙水壓力響應稍有滯后。其原因與圖5相同，在此不在贅述。此外，對比圖6中的四幅圖可看出，隨入射頻率的增加，整體孔隙水壓力變小。

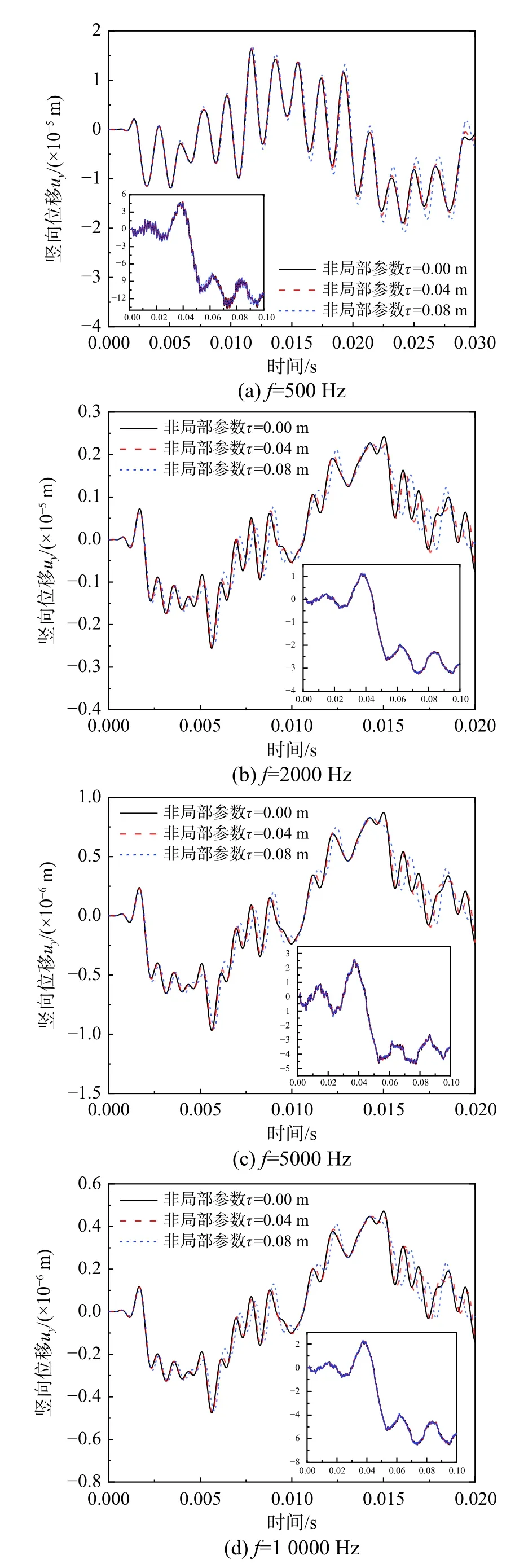
圖5 不同荷載頻率下一維飽和土地基位移響應時程曲線Fig.5 The displacement time-history curve of the onedimensional saturated foundation for different load frequency

圖6 不同荷載頻率下一維飽和土地基孔壓響應時程曲線Fig.6 The pore-pressure time-history curveof the onedimensional saturated foundation for different load frequency

3.2.2循環荷載下二維飽和土地基動力響應

為充分研究孔隙尺寸效應對飽和土地基動力響應的影響，本節采用如圖3的循環荷載下飽和土地基的計算模型尺寸，但在模型左端1m 范圍內作用有均勻分布的正弦荷載，荷載周期為T，荷載頻率取為1000Hz。模型底面為固定且不透水邊界，左右邊界為自由且排水邊界(不對土骨架位移及流體相對土骨架位移施加任何約束)。觀測點位于距離模型右側10m 處的A點(地表)和模型表面中心B點。本實例飽和土所采用物理力學參數見表2中的材料2。

圖7和圖8分別為循環動荷載下觀測點B和觀測點A的固體位移及流體相對固體位移的時程曲線，由圖可知，時間小于1.6×10-2s時，觀測點B的位移響應為0，這是由于左端均布荷載產生的波還未到達觀測點B，隨時間的增加，觀測點B開始波動，但考慮非局部效應，B點出現波動的時間稍有延遲，且隨著時間的增加位移響應的延遲愈加明顯。該現象也可從觀測點A看出，所不同的是A點產生波動的時間大約在3×10-2s時刻。從圖中還可以看出，考慮孔隙尺寸效應對飽和土介質中位移場的幅值影響不大，只是對飽和土介質中波速影響較大，由此導致位移場的相位差發生變化。由此說明，孔隙尺寸效應對循環荷載所引起地基中的能量影響較小。此外，由圖中的插圖可知，隨時間的增加，位移場波動幅值略有增加的趨勢，這是由于所施加的動載的持續作用，在介質中的能量積累所致。

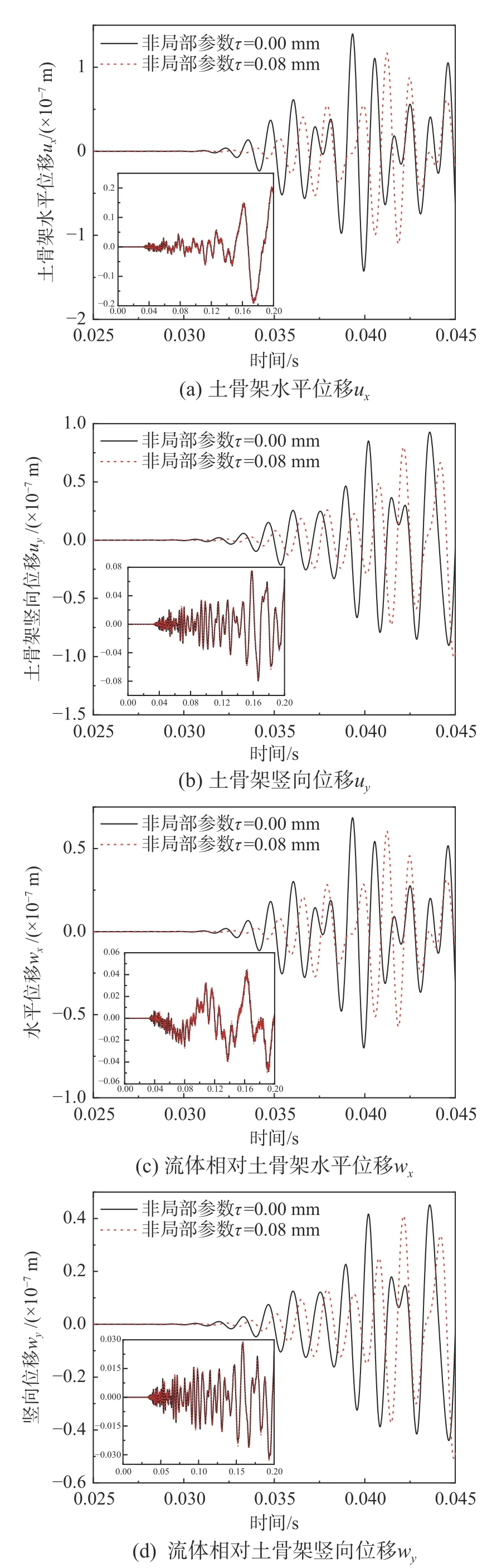
圖7 觀測點A的位移時域響應Fig.7 Displacement response in time domain at point A

圖8 觀測點B 位移時域響應Fig.8 Displacement response in time domain at point B

3.2.3循環荷載下飽和土地基動力響應

本節例子所模擬的是一個飽和土地基，在其中心處作用一個均勻分布荷載P，荷載隨時間呈正弦變化。考慮到該問題的對稱性，僅考慮一半模型，如圖9所示。約束模型兩側及底部的法向位移，且模型兩側及底面為不透水邊界條件。模型的幾何參數及網格劃分如圖9所示，物理力學參數見表3.2中的材料3。正弦荷載幅值為100 kPa，振動頻率為1000 Hz，Newmark 積分步長選取為Δt=1.0×10-5s，即所分析的時長為3×10-2s。本節主要分析，非局部參數對循環荷載下飽和土地基位移及孔壓響應的影響，觀測點位于模型的四個頂點，順時針方向依次為點1、點2、點3及點4(如圖9所示)。

圖9 條形荷載作用下地基響應計算模型Fig.9 Calculating modelof the responseof foundation subjected to a strip load

圖10為循環荷載下觀測點1和2處位移時程曲線，表征孔隙尺寸效應的非局部參數分別取為?0=0.00 m 和?0=0.08m。由圖可知，觀測點1的位移響應隨時間的增加呈現出波動上升的趨勢，而考慮非局部參數后，位移響應相對于經典Biot 理論(非局部參數取0)的計算結果有向后延遲現象，其原因是由于觀測點1距離荷載作用區域有一定的距離，而考慮非局部效應后飽和土中波速有所降低所致。而觀測點2位于荷載的下方，因此隨時間增加位移場的相位差相差不大，但其振動幅值有一定程度的減小。

圖10 位移時程曲線Fig.10 Displacement time-history curve

圖11為循環荷載下，上述四個觀測點的孔壓隨時間變化曲線，由圖可看出，觀測點1、觀測點2和觀測點4孔壓響應開始時間有不同程度的延遲，其原因為各觀測點與荷載的距離不同，導致其產生響應的時間不同。由于觀測點2正好位移荷載下方，因此，孔壓響應沒有延遲現象，且考慮及不考慮孔隙尺寸效應所引起孔壓響應的相位基本一致。此外，考慮孔隙尺寸效應后，觀測點1的孔壓振動幅值有一定的增大，而觀測點2、觀測點3和觀測點4處孔壓幅值則呈現出不同程度減小，且孔壓響應均有滯后的現象。

圖11 孔壓時程曲線Fig.11 Pore pressure time-history curve

4 結論

本文基于非局部Biot 理論，采用虛位移法構建了有限元空間離散方程，采用Newmark 積分法對時間進行了離散，并采用MATLAB軟件編制了飽和土地基二維動力固結的有限元計算程序，通過與解析解及已有的單相介質數值解的對比，驗證了本文有限元計算程序的正確性。進而，采用該有限元程序分析了三種典型的工程實例，得出如下結論：

(1)荷載頻率振動頻率較低時，非局部Biot 理論與經典Biot 理論所預測的結果差別很小，即非局部參數的影響很小；

(2)當輸入高頻荷載時，孔隙尺寸效應的影響逐漸顯現，且非局部參數對位移和應力響應的相位產生顯著影響，使得位移場及孔壓的響應時間有所延遲。這是由于考慮孔隙尺寸效應后，飽和土中的波速有所降低，由此導致荷載在飽和土中引起的波傳播至觀測點的時間有所延長，從而引起位移及孔壓延遲響應的現象。

本文的數值模型可以用于研究如廠房機械振動、高速鐵路、高速公路地基的動力響應及固結沉降分析等飽和土動力響應及固結沉降問題。