經歷抽象過程 發展數學素養

馮想麗

［摘? 要］ 在高中數學教學中，為了便于學生更好地理解數學、應用數學，教師可引導學生借助觀察、交流、抽象等學習活動來積累數學經驗，豐富數學認知體系，以此讓學生掌握數學研究方法，有效提升數學素養.

［關鍵詞］ 理解數學；應用數學；數學素養

在高中數學教學中，多數教師認為概念、公式、定理等基礎知識為客觀事實，只要學生熟記并結合一些具體練習就能實現知識的內化，因此常常以“講授”為主. 單一的講授雖然能夠確保教學進度，但因為沒有引導學生經歷獨立思考和合作探究的過程，學生對這樣得到的知識難以形成深刻認識，導致他們很難靈活應用相關知識去解決問題. 這顯然不利于教師教學目標的實現，不利于學生學習能力的提升. 教學概念、公式、定理等基礎知識時，教師應帶領學生多經歷一些思考過程，在幫助他們夯實基礎的同時，全面提升他們的思考能力、分析能力、應用能力等綜合能力.

談起函數概念，高中生普遍認為抽象、難懂，雖然初中階段就作為重點內容講解過，但是讓學生用集合語言來刻畫變量間的依賴關系時，大部分學生會感覺不適. 而函數是高中數學教學的重點，其與方程、不等式、數列等內容緊密相連，貫穿高中數學學習始終，這要求教師在函數的概念教學中不能蜻蜓點水，而要通過深度剖析，讓學生掌握其本質和核心，從而為后續學習打下堅實的基礎. 筆者在函數的概念教學中，結合具體實例與學生共同經歷了概念抽象的過程，讓學生積累數學活動經驗的同時提升了數學素養. 從教學反饋來看，學生既能用準確的數學語言來表述，又能靈活應用概念去解決問題，而且課堂參與度較高，取得了較好的效果. 筆者現將教學過程呈現給大家，若有不足，請指正.

教學實錄

1. 借助情境，回憶舊知

師：在現實生活中，很多變化都體現了一種“依賴關系”，你能簡單地列舉幾個實例嗎？

生1：一個人的知識儲備與他的學習時長.

生2：拉橡皮筋的時候，用的力氣越大拉得越長.

……

師：大家說得都非常好，在初中階段我們是用什么來刻畫這種“依賴關系”的呢？

學生齊聲答：函數.

師：很好，現在請大家回憶一下，初中階段我們是如何來定義函數的？

設計意圖 以學生熟悉的情境入手，通過舊知回顧激活學生的原有認知，為接下來的“再創造”奠定基礎.

從課堂反饋來看，多數學生知道變量間的依賴關系，并能用一些常用的函數，如一次函數、反比例函數等進行說明，但還不能用準確的數學語言來刻畫. 函數概念的教學是在學生原有認識上的建構，學生對舊知的掌握情況直接影響著本節課的教學效果，因此教師有必要帶領學生回顧舊知. 教師可先讓能夠完整敘述概念的學生講述一遍，然后用PPT給出概念，同時預留一定的時間讓學生去回顧記憶，并引導學生理解定義中x與y的對應關系，為接下來概念的拓展做好鋪墊.

2. 回顧舊知，發展新知

師：請大家結合初中所學的函數的定義思考下列問題.

例1 某部隊在實戰演習中發射了一枚炮彈，已知炮彈距地面的高度h（單位：m）與發射時間t（單位：s）滿足關系式h=130t－5t2. 那么是否可以說明h為關于t的函數呢？

生3：是的，根據函數的定義，對于變量t的每一個值，都有唯一的h值與之對應.

師：如何對應的呢？

生3：按照關系式h=130t－5t2.

師：很好，既然是對應的，你能算一算當t=2時，h為何值嗎？

生4：當t=2時，h=240.

師：當t=4時，h又為何值呢？

學生齊聲答：440.

師：當t=20.5時呢？

生5：可以算，但是這個太復雜了吧.

師：確實，這個算起來有點煩瑣，看來大家都不想算，那么你們能不能創造一個簡單的符號來表示呢？（生沉思）

師：例如“h（t=20.5）”. （學生感覺無從入手，筆者給予鼓勵和提示誘發學生積極思考和表達）

生6：h.

師：還有嗎？

生7：h（20.5）.

……

師生共同交流后最終統一認為用“h（20.5）”來表示更加簡潔、易懂.

師：那么大家再思考一下，若t=t，h為何值呢？

學生齊聲答：h（t）.

師：很好，你們真的太棒了！

設計意圖 在學習過程中，很多學生表示對于符號y=f（x）難以理解，這樣通過交流能使學生初步認識符號y=f（x）.

師：相信對于定義域和值域大家都不陌生，本題中自變量t和因變量h的取值范圍分別是什么？你能用集合來表示嗎？（定義域和值域是學生較為熟悉的內容，很快就有學生給出了答案）

生8：t的取值范圍為｛t0≤t≤26｝，h的取值范圍為｛h0≤h≤845｝.

師：你是如何求的？

生8：我是根據函數圖象來判斷的，h=130t－5t2為二次函數. 因為h≥0，所以0≤t≤26，而當t=13時，到達最高點，此時h=845.

師：對于h≥0你是如何判斷的呢？

生8：根據已知并聯想生活實際很容易知曉這個道理，因為炮彈落地就炸了.

師：確實，如果落地不爆炸，想飛多久就飛多久，這個后果可就難以預料了. （學生笑）

師：若t的取值范圍用A表示，h的取值范圍用B表示，你能嘗試用集合語言來刻畫h與t的對應關系嗎？

生9：對于集合A中的任意一個元素t，在集合B中都有唯一的元素h與之對應.

就這樣，在筆者的鼓勵和引導下，函數概念初步形成，學生由原有的依賴關系逐漸向對應關系轉化，尤其是集合的引入，為接下來學生進一步理解與區分映射關系奠定了基礎.

3. 借助實例，逐漸抽象

師：結合例1，接下來我們一起分析下面這個問題，是否還可以像剛剛那樣來研究呢？

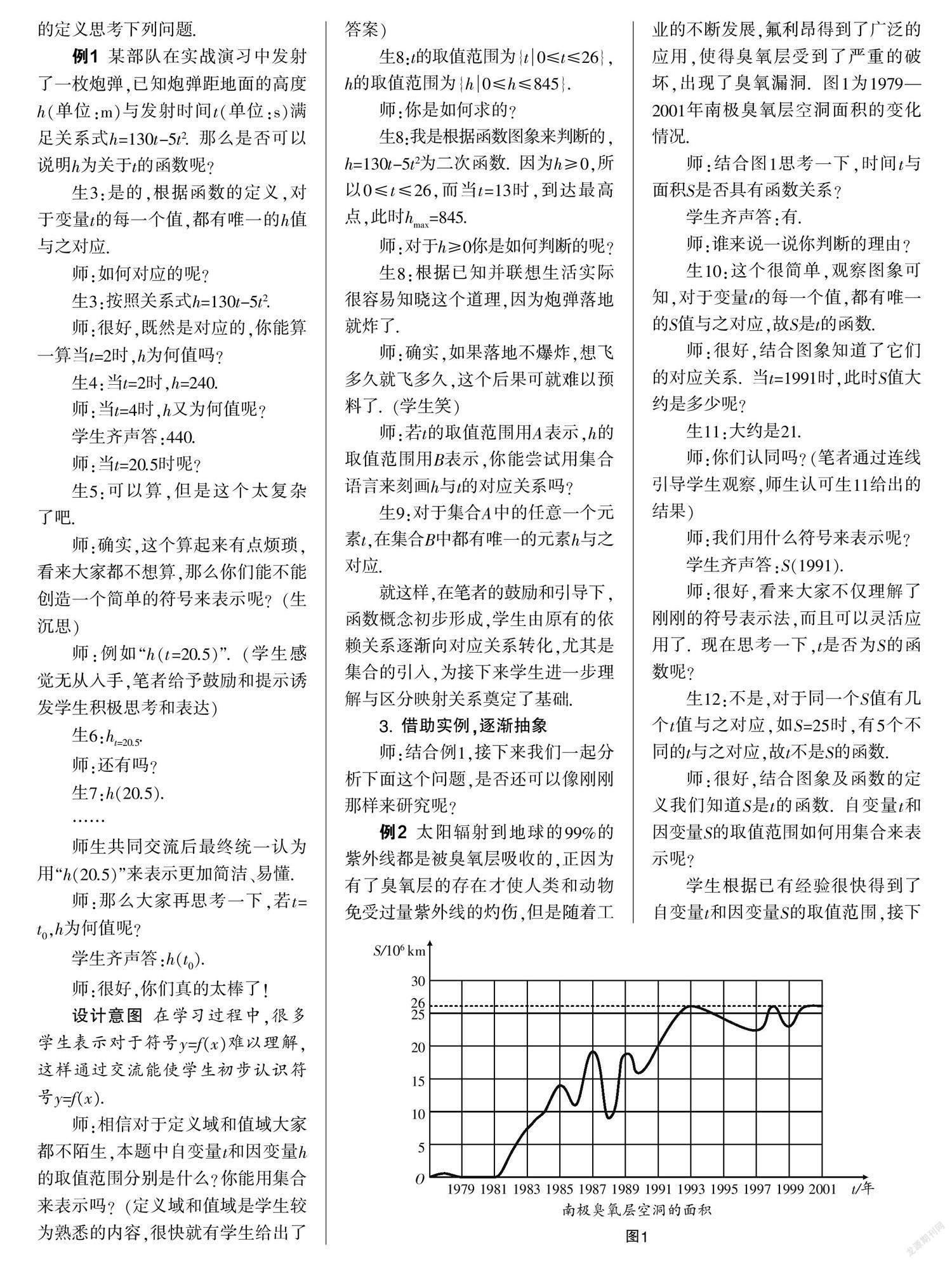
例2 太陽輻射到地球的99%的紫外線都是被臭氧層吸收的，正因為有了臭氧層的存在才使人類和動物免受過量紫外線的灼傷，但是隨著工業的不斷發展，氟利昂得到了廣泛的應用，使得臭氧層受到了嚴重的破壞，出現了臭氧漏洞. 圖1為1979—2001年南極臭氧層空洞面積的變化情況.

師：結合圖1思考一下，時間t與面積S是否具有函數關系？

學生齊聲答：有.

師：誰來說一說你判斷的理由？

生10：這個很簡單，觀察圖象可知，對于變量t的每一個值，都有唯一的S值與之對應，故S是t的函數.

師：很好，結合圖象知道了它們的對應關系. 當t=1991時，此時S值大約是多少呢？

生11：大約是21.

師：你們認同嗎？（筆者通過連線引導學生觀察，師生認可生11給出的結果）

師：我們用什么符號來表示呢？

學生齊聲答：S（1991）.

師：很好，看來大家不僅理解了剛剛的符號表示法，而且可以靈活應用了. 現在思考一下，t是否為S的函數呢？

生12：不是，對于同一個S值有幾個t值與之對應，如S=25時，有5個不同的t與之對應，故t不是S的函數.

師：很好，結合圖象及函數的定義我們知道S是t的函數. 自變量t和因變量S的取值范圍如何用集合來表示呢？

學生根據已有經驗很快得到了自變量t和因變量S的取值范圍，接下來筆者又引導學生用集合的語言來刻畫t與S的函數關系. 經過以上兩個問題的過渡，學生對函數符號以及用集合語言刻畫函數有了深刻并明晰的認識，整個過程隸屬學生的認知范疇，因此學生學起來得心應手，課堂氛圍自然流暢，學生的學習積極性也被充分地調動了起來，為接下來定義的抽象做好了鋪墊.

4. 逐層遞進，自然生成

師：剛剛結合圖象我們得出了S是t的函數的結論，不知道通過表格我們是否能發現點什么？（學生迫不及待地想探究新問題）

例3 國際上常常用恩格爾系數來反映人民的生活質量，恩格爾系數=食物支出金額÷總支出金額. 你們認為是系數越大生活質量越高，還是系數越小生活質量越高呢？（學生存在一定的意見分歧，筆者引導學生聯想家庭支出，從而統一了認識，即系數越低，生活質量越高）

師：表1為某地城鎮恩格爾系數變化情況. （筆者用PPT展示表1）

師：若時間和恩格爾系數分別用m和n表示，m與n是否具有函數關系？

生13：我認為n是m的函數，但m不是n的函數，因為對于變量m有唯一n值與之對應，但是對于變量n，其對應的m值不唯一，如當n=30.1時，m就有兩個不同的值，分別為2013和2016.

師：觀察得很仔細，表述得也非常準確，很好. 那么m與n是如何對應的呢？如何用集合語言來描述呢？

生14：通過表格可見其對應關系. 對于集合A中的任意一個元素m，在集合B中都有唯一的元素n與之對應.

師：如果讓你寫出集合A，B中的元素，你會寫嗎？

生14：A=｛2008，2009，2010，2011， 2012，2013，2014，2015，2016，2017｝，B=｛37.9，36.5，35.7，36.3，36.2，30.1，30，

29.7，30.1，29.3｝. （筆者投影展示學生得到的結果）

師：思考一下，以上三個實例是如何用集合語言來描述的？它們有什么共同點？你能否用一句話來總結一下？（筆者預留時間讓學生進行概括、抽象）

生15：根據某種對應關系，對于集合A中的任意一個元素x，在集合B中都有唯一的元素y與之對應.

師：如果某種對應關系用符號來表示，你會嗎？（學生在課前進行了預習，很快給出了符號“f”）

在筆者的帶領下，學生自主完成了問題的總結和概括，相信經過觀察、分析、總結等過程，學生對“對應關系”會形成深刻的印象. 經歷以上刻畫的過程后，學生能順暢地、完整地表述函數概念.

師：如果既要直觀地呈現集合中的元素x和y，又要體現對應關系f的作用，你能構造一個數學符號來表示嗎？（學生結合剛剛的探究經驗，很快給出了結果）

學生齊聲答：y=f（x）.

接下來，筆者用PPT完整地呈現了函數概念. 因經歷了概念形成的全過程，學生面對抽象的概念時鎮定自若，一改往日的焦慮，可見引導學生參與知識形成的過程是很有必要的.

5. 融于練習，彰顯本質

師：接下來我們利用幾個練習來體驗一下. （筆者用PPT給出題目）

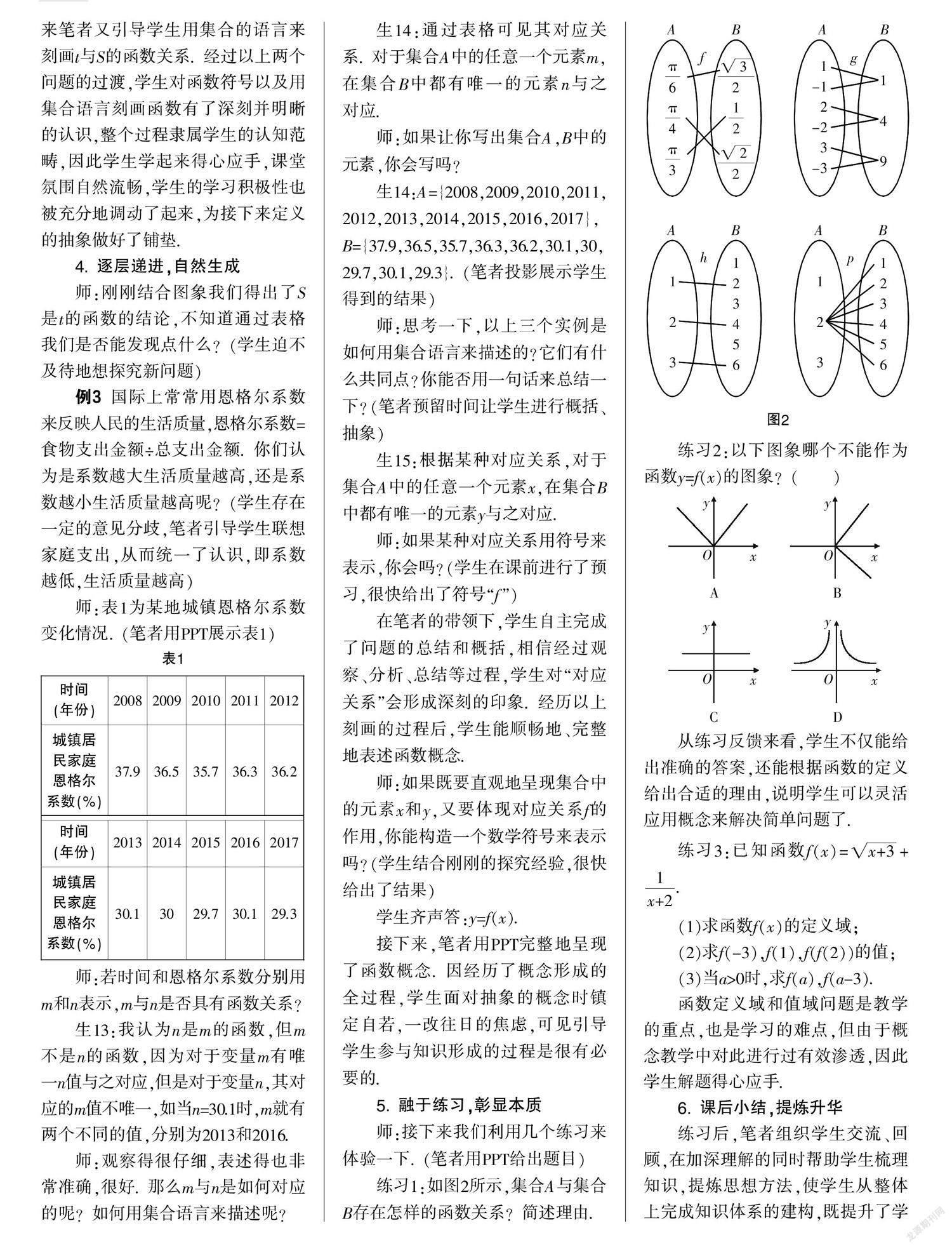
練習1：如圖2所示，集合A與集合B存在怎樣的函數關系？簡述理由.

練習2：以下圖象哪個不能作為函數y=f（x）的圖象？（ ?）

從練習反饋來看，學生不僅能給出準確的答案，還能根據函數的定義給出合適的理由，說明學生可以靈活應用概念來解決簡單問題了.

練習3：已知函數f（x）=+.

（1）求函數f（x）的定義域；

（2）求f（－3），f（1），f（f（2））的值；

（3）當a>0時，求f（a），f（a－3）.

函數定義域和值域問題是教學的重點，也是學習的難點，但由于概念教學中對此進行過有效滲透，因此學生解題得心應手.

6. 課后小結，提煉升華

練習后，筆者組織學生交流、回顧，在加深理解的同時幫助學生梳理知識，提煉思想方法，使學生從整體上完成知識體系的建構，既提升了學生的學習能力，又增強了學生的學習信心，還提升了學生的核心素養.

教學反思

學生的認知水平和思維能力發展正如函數關系一樣，會隨著學習時間、學習的努力程度等因素的變化而變化，因此教師必須認識到學生學習能力的提升需要經歷一個過程. 教師教學時不能急于求成，應帶領學生參與到知識的生成和發展中來，進而通過切身體驗完成知識體系建構.

高中的函數概念是基于初中函數概念發展的，并非重新定義. 在教學中，筆者先引導學生回顧舊知，并在此過程中進一步抽象，如先是表達式對應，再是圖象對應，最后是表格對應，由三種不同的對應關系逐漸抽象出對應符號“f”；又如從自變量和因變量的取值范圍出發，逐漸引導學生由具體集合逐漸抽象為符號集合，讓學生經歷由特殊到一般、由具體到抽象的活動過程后，重新認識函數概念，掌握數學研究方法，提升數學思維能力.

另外，教學中筆者先引導學生借助已有經驗來判斷函數關系，再引導學生用集合語言進行描述，通過逐層深入的教學方式有效地淡化了概念的抽象感. 對于符號的表示一直是教學難點，為了突破此教學難點，筆者借助“當t=20.5，h為何值”激發學生引入數學符號來表示h值的緊迫感. 這樣做既為符號y=f（x）的引入做好了鋪墊，又有助于學生理解符號y=f（x）. 整個過程自然流暢，巧妙地化解了教學難點，在潛移默化中發展和提升了學生的學習能力.

總之，在數學教學中，教師要善于借助一些具體問題或探究活動來調動學生的積極性，鼓勵學生自主解決問題，讓學生在解決問題的過程中完成知識的梳理，既能強化學生的數學學習能力，又能提升學生的數學核心素養.