精心設計問題鏈 以生為本促“雙減”

劉建

【摘要】隨著“雙減”政策的逐步落實，學生的作業負擔和校外培訓負擔明顯減輕.為了做到減負提質，提高課堂教學效率成為關鍵.課堂中，教師通過精心設計問題鏈，對學生進行啟發引導，把學習的主動權交給學生，讓學習真正發生，體現以生為本，從而實現課堂效率和教學質量的提高.

【關鍵詞】問題鏈；以生為本；“雙減”

【基金項目】江蘇省中小學教學研究第14期立項課題“初中數學‘鏈+課堂的實踐研究”（2021JY14-L398）.

一、教學背景

如皋市吳窯鎮吳窯初級中學一直堅持落實立德樹人這一根本任務，打造“愛的教育”品牌，鼓勵全體教師做有溫度的教育，當有情懷的教師.“雙減”之后，學生的作業負擔和校外培訓負擔確實明顯減輕，但減負并不是“雙減”的最終目的，讓學生在學校里就能學足學好，提高學校教學質量才是“雙減”政策的目標.學校教學的主陣地在課堂，因此切實提高課堂教學效率成為落實“雙減”政策的關鍵.

在課堂中以生為本，把學習的主動權交給學生，讓學習真正發生，這就是“愛的教育”的真正體現.筆者認為，教師通過精心設計問題鏈，對學生不斷進行啟發引導，就能讓“以生為本”落到實處，讓“雙減”政策落地落實.文章擬以人教版八年級上冊“14.2.1平方差公式”的教學為例，淺談“雙減”背景下數學課堂如何做到以生為本.

二、教學目標

本節課是“14.2乘法公式”的起始課，因此筆者將本節課的教學目標設置為：

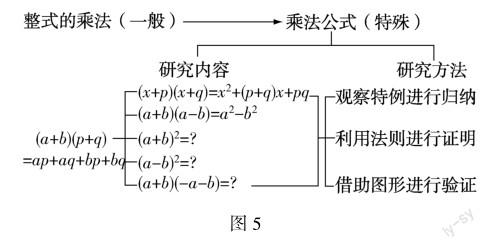
（1）通過回顧特殊形式的多項式相乘，展望乘法公式單元的研究內容和研究方法，構建乘法公式單元知識體系，豐富數學活動的經驗和體驗.

（2）通過平方差公式的發現、推導、驗證和應用，使學生體悟知識方法的生成過程和應用價值，激發學生的主觀能動性，進一步培養其邏輯思維能力和推理論證能力.

三、教學設計

（一）從一般到特殊，展望研究內容

問題2：仔細觀察這些式子，兩個括號中的多項式有什么聯系和區別？你認為多項式與多項式相乘有哪些特殊形式？（先獨立思考，再小組交流）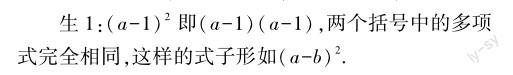

生2：（a+3b）（a-3b），兩個括號中的多項式一項相同，另一項互為相反數，這樣的式子形如（a+b）（a-b）.

生3：第2題所有式子兩個括號中的多項式一項相同，另一項不同，這樣的式子形如（x+p）（x+q）.

問題3：結合平時完成的練習，兩個項數為2的多項式相乘還有其他特殊形式嗎？

生4：（a+b）2.

生5：（a+b）（-a-b）.

【設計意圖】乘法公式的運用是在學生已經學過整式乘法的基礎上進行的，從一般的多項式乘多項式出發，教師讓學生尋找其特殊形式，在回顧舊知的基礎上對即將研究的內容進行展望，讓學生在學習之前對整個單元有一個整體概念，同時在此過程中也滲透了分類討論和從一般到特殊的數學思想方法.

（二）借助已有方法，開展公式探究

1.觀察特例，歸納規律

問題4：今天我們研究第二個式子（a+b）（a-b），請同學們舉幾個符合該特征的式子，并利用多項式與多項式相乘的法則計算出結果.

生6：（x+2）（x-2）=x2-4.

生7：（1+3a）（1-3a）=1-9a2.

生8：（x+5y）（x-5y）=x2-25y2.

問題5：觀察上述等式，你發現了什么規律？

（一段時間后，教師發現不少同學還存在疑問，于是設置子問題進一步啟發引導.）

子問題1：等式左邊的式子有什么特征？

生9：等式左邊兩個括號中的第一個數和第二個數都相同，中間的符號不同.

生10：等式左邊是兩個數的和乘這兩個數的差.

生11：等式左邊兩個括號中的兩項，一項相同，另一項互為相反數.

生12：等式左邊可以寫成（a+b）（a-b）的形式.

子問題2：等式右邊的式子有什么特征？

生13：等式右邊的兩項是兩個數平方的差.（師：即兩個數的平方差.）

生14：等式右邊的第一項是等號左邊括號中第一個數的平方，等式右邊的第二項是等號左邊括號中第二個數的平方.

生15：等式右邊可以寫成a2-b2的形式.

子問題3：你能用文字或符號總結這一規律嗎？

生16：用文字可以表述為：兩個數的和與這兩個數的差的積，等于這兩個數的平方差.

生17：用符號表述為（a+b）（a-b）=a2-b2.

【設計意圖】有前面學習的經驗，無論是舉符合特征的例子，還是觀察所得等式歸納規律，對學生來講都屬于最近發展區里的內容，這些都可以由學生自己完成.在學生回答某些問題存在困難時，教師要設置子問題，鋪設臺階，進一步啟發引導.教師讓不同的學生用不同的表達方式嘗試歸納規律，能有效讓所有學生逐漸加深對公式的理解.

2.運用法則，證明公式

問題6：這個等式就能作為公式使用嗎？（大部分學生遲疑）

追問：剛才我們是怎樣得到這個等式的？

生18：我們是通過觀察幾個特殊例子總結得出上面的等式的.

生19：哦，幾個特殊例子不能代表所有的式子.

生20：我們也不可能窮盡所有這樣的式子，所以我們必須想辦法給出證明.

問題7：那么我們應該如何證明呢？（學生獨立完成，然后小組交流）

生21：我們可以利用多項式與多項式相乘的法則進行（a+b）（a-b）=a2-ab+ab-b2=a2-b2.

生22：我們還可以利用公式（x+p）（x+q）=x2+（p+q）x+pq進行，（a+b）（a-b）=a2+（b-b）a-b2=a2-b2.

追問：為什么可以用第二種方法證明？

生23：今天所學的（a+b）（a-b）不僅是（a+b）（p+q）的特殊形式，還是（x+p）（x+q）的特殊形式.

師：通過證明，該等式是成立的，我們把這個公式稱為平方差公式.

【設計意圖】學生對于證明的必要性很模糊，對于代數證明的必要性則更加模糊.教師通過提問和追問，讓學生明白通過觀察特例歸納出來的結論未必正確，必須經過嚴格證明才行.公式證明對于學生來講相對較為容易，這里主要是讓學生進一步體會一般到特殊的數學思想方法，一般形式所具有的方法特殊形式一定具有.

3.構造圖形，驗證公式

問題8：你能構造出圖形說明平方差公式嗎？（學生思考片刻，但很多同學沒有頭緒）

追問1：前面我們是怎樣利用圖形面積的方法說明公式（x+p）（x+q）=x2+（p+q）x+pq的？

生24：構造出圖1中的圖形，把等式左邊看成長為（x+p），寬為（x+q）的長方形的面積，右邊則是4個小長方形的面積.

追問2：那么平方差公式的左右兩邊的這些式子可分別看成哪些圖形的面積？

生25：（a+b）（a-b）可看成長為（a+b），寬為（a-b）的長方形的面積.

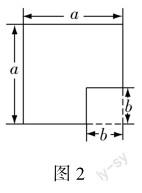
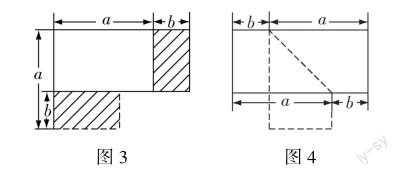
生26：a2可看成邊長為a的正方形的面積（教師拿出邊長為a的正方形模型），b2可看成邊長為b的正方形的面積（教師拿出邊長為b的正方形模型，其中b

追問3：那么平方差公式右邊可以理解成什么圖形的面積？

生27：可以理解為從大正方形中減去小正方形后所得圖形的面積.

（師生用剪刀進行操作并在黑板上畫出圖2）

追問4：對照等式左邊，接下來需要干什么？

生28：把這個圖形剪拼成一個長為（a+b），寬為（a-b）的長方形.

追問5：請同學們動手畫一畫，想一想應該如何剪拼？

生29：如圖3，我們可以剪掉陰影部分的長方形，再補到右邊，從而得到符合要求的長方形.

生30：如圖4，我們可以剪下虛線部分的梯形，再把兩個梯形拼成如圖所示的長方形.

【設計意圖】問題8難度較大，筆者并沒有直接給出課本中的圖，而是首先回顧已學公式的圖形面積驗證方法，然后讓學生模仿、類比，由式思形，再讓學生進行剪拼，把整個構造圖形的過程全部交給學生.教師不越俎代庖，所起的作用僅是啟發引導.讓學生獨立構造有一定難度，教師需要通過不斷追問，引導學生回憶相關舊知，領悟方法，鋪設臺階，動手操作，啟迪思維，并利用不同的方法解決問題.

（三）通過小結提升，繼續展望新知

問題9：通過這節課的學習，你有哪些收獲？（略）

問題10：你覺得我們接下來將研究什么？（略）

本節課部分板書如下：

【設計意圖】教師通過小結，讓學生鞏固所學知識，知道使用平方差公式的注意事項，進一步強化乘法公式的研究方法，了解接下來需要研究的內容.在本節課中，教師設計了一些不可以運用平方差公式的問題，讓學生認識到它們也具有特殊性，利用本節課的研究方法學生可以開展獨立探究.本節課的板書設計有利于學生構建乘法公式單元的知識體系.

四、教學反思

（一）把學習的主動權還給學生

本節課中教師通過精心設計的問題鏈，不斷啟發引導學生，在與學生反復問答、深層互動中，水到渠成地生成知識和方法.知識方法是在啟發過程中自然生成的，不是教師反復敲黑板告訴學生的，學生真正理解了，因此不容易遺忘.在不斷啟發中學生搞清了知識方法的來龍去脈，重視知識方法的生成過程；在不斷啟發中教師了解學生的實際情況，然后對癥下藥，針對學生出現的問題及時調整教學思路；在不斷啟發中教師引導學生思考，啟迪學生的智慧，從而實現“培優”；在不斷提問、追問中，教師夯實了學生的知識基礎，從而實現“補差”.因此，這樣的課堂真正體現了以生為本，讓每一名學生在課堂中都能學有所獲，都能得到應有的進步，真正體現了教師對每一名學生的關愛.

（二）有利于優化學生認知結構

問題1至問題3通過尋找特殊形式的多項式相乘，使學生明確“乘法公式”單元的研究內容，問題4至問題8借助于已有的研究方法，展開對平方差公式的探究，問題9至問題10讓學生通過議論、小結和提升，達到準確運用平方差公式的目的并展望即將學習的內容.這樣做既有助于學生知識結構的整體形成，也有利于學生對運用平方差公式進行計算的整體把握.

【參考文獻】

[1]中華人民共和國教育部.義務教育數學課程標準（2022年版）[M].北京：北京師范大學出版社，2022.

[2]印冬建.初中數學“鏈+”課堂的建構與思考：以“15.1.1從分數到分式”為例[J].中學數學，2020（16）：17-20.

[3]黃驥飛.巧借分層變式提升學習能力：以“平方差公式”的教學設計為例[J].數學大世界（上旬），2022（12）：30-31.