基于Q學習的多無人機協同航跡規劃方法

尹依伊， 王曉芳， 周健

(1.北京理工大學 宇航學院， 北京 100081； 2.北京電子工程總體研究所， 北京 100854；3.西安現代控制技術研究所， 陜西 西安 710065)

0 引言

多飛行器協同作戰是未來空戰的重要發展趨勢，與單飛行器相比，多飛行器具有更高的作戰效能以及更強的作戰能力[1]。在多飛行器協同飛行過程中，航跡規劃技術可為飛行器提供航跡指引，是實現飛行器協同作戰的關鍵技術之一[2-4]。協同航跡規劃可得到滿足飛行器性能約束及時間協同約束的最優航跡，是多飛行器實現自主飛行的重要保障[5]。好的航跡不僅能節省飛行器運行的成本，也增加了完成攻擊任務的成功率[6]。

針對協同航跡規劃問題，國內外學者進行了較多研究。文獻[7]提出了一種在混合衛星導航覆蓋場景中的多無人機路徑規劃方法，使各無人機能夠在同一空間內共存且彼此不發生碰撞，仿真結果表明無人機數量增多對計算負擔幾乎無影響。文獻[8]提出了帶距離因子的改進勢場法，此算法能夠在三維環境下控制多無人機避開障礙物，到達期望位置。文獻[9]建立了一種基于無向圖搜索方法的覆蓋路徑優化模型，并通過混合整數線性規劃方法求解各無人機的最優飛行路徑。文獻[10]提出飛行無人機能量因子概念，并基于遺傳算法設計了一種用于多無人機的能量平衡路徑規劃算法，以使多無人機協同完成搜索和救援任務。文獻[11]針對現有路徑規劃方法忽略偵察區域優先級的問題，將偵察區域、人機能耗和飛行風險值加權作為多目標效能函數，基于粒子群優化算法求解多無人機的最優協同偵察路徑。但上述文獻均未對時間協同問題進行考慮。文獻[12]利用羊群算法求解滿足時間協同與空間協同的航跡組，但此算法僅適用于環境模型已知的路徑規劃問題，當環境發生突變時需要重新進行求解。文獻[13]考慮到固定和移動目標、外部干擾等情況，使用粒子群優化算法求解得到避免碰撞的最佳路徑。

隨著人工智能領域的發展，強化學習技術也被應用于多智能體協同航跡規劃中。文獻[14]針對追捕問題，提出了一種基于共享經驗的Q學習航跡規劃算法，此算法具有收斂速度快的優點。文獻[15]考慮了飛行時間和碰撞避免約束，基于深度強化學習理論設計了在沒有密集無線信道特性先驗知識情況下的協同航跡規劃方法，但此算法所需求解時間較長，不適用于在線應用的場景。文獻[16]提出了一種聯合動作- 狀態法，與環境交互時各智能體采取聯合狀態與聯合動作，此方法有效減少了探索次數，但存在維度爆炸的問題。文獻[17]提出了一種基于多智能體深度確定性策略梯度算法，通過同步目標分配和路徑規劃，避免重分配帶來的重規劃問題，提高了路徑規劃效率，但此算法所需訓練時間較長。文獻[18]基于改進的深度Q學習(DQN)算法解決多機器人路徑規劃問題，與傳統DQN算法相比具有更快的收斂速率，但此方法也存在求解時間較長的問題。

本文首先建立了航跡規劃問題的馬爾可夫模型，基于Q學習理論設計了單飛行器的航跡規劃算法，針對多飛行器航跡規劃的時間協同問題，根據Q學習理論的特點，將單飛行器航跡規劃的經驗矩陣拓展到多飛行器圍捕目標的協同航跡規劃中，設計了滿足時間協同約束的多飛行器航跡規劃方法。然后針對飛行器間碰撞避免問題，通過設計后退參數并基于深度強化學習法設計了碰撞段局部航跡重規劃方法，實現了多飛行器間的避碰目標。考慮航跡規劃問題的在線應用問題，針對環境中存在先前未探明障礙物的情況，設計障礙物Q矩陣，通過將障礙物矩陣與原經驗矩陣疊加的方法，使飛行器能夠在線躲避新探測到的障礙物。最后進行了多飛行器協同航跡規劃的仿真，證明了所述算法的正確性與有效性。

1 基于Q學習的單無人機航跡規劃方法

1.1 航跡規劃問題馬爾可夫建模

將無人機航跡規劃的Q學習問題建模為馬爾可夫決策過程，依次對環境、狀態S、動作A、回報R及策略進行如下定義。

1.1.1 環境模型描述

采用柵格法對環境進行離散化處理，假設無人機勻速飛行，且飛行速度為v，法向加速度幅值為azmax，則其最小轉彎半徑Rm為

(1)

為了使規劃的航跡具有可飛性，即無人機能夠在相鄰柵格內實現連續轉彎運動，因此需滿足柵格邊長l大于最小轉彎半徑的4倍(l≥4Rm)。在考慮無人機機動能力的前提下，考慮到環境建模的精確性，取l=4Rm。假設作戰空間長度為L、寬度為W，則離散化處理后柵格子空間個數N為

N=L4Rm?W4Rm

(2)

式中：「?表示向上取整。因此，離散化處理后的戰場區域可能略大于實際作戰區域。

無人機從初始位置向位于期望位置的目標飛行，環境建模示意圖如圖1所示。圖1中，紅色區域為期望位置，黑色區域為障礙禁行區域，藍色區域為無人機的初始位置，局部放大區域為柵格邊長與最小轉彎半徑的關系示意圖。

圖1 戰場模型示意圖Fig.1 Diagram of battlefield model

1.1.2 狀態空間、動作空間設計

針對航跡規劃問題，將狀態S與無人機位置建立聯系，當環境模型如圖1所示時，作戰空間被劃分為144個柵格，依次對柵格進行標號，將無人機視為質點，無人機所處柵格作為無人機狀態。如圖2所示，無人機離散化后的動作空間選取為向上、向下、向左和向右4個飛行方向。

圖2 動作空間示意圖Fig.2 Diagram of action space

當無人機執行所選動作后，其狀態轉移到對應相鄰狀態，實現動作狀態的轉移，因此，Q學習滿足馬爾可夫性質，即下一時刻狀態只與當前狀態有關，與之前狀態無關。

1.1.3 回報函數設計

針對單無人機的航跡規劃問題，本文設計回報函數為

(3)

式中：a、c為大于0的常數。回報函數體現了對無人機向期望位置飛行的牽引作用和對障礙的回避作用。

1.1.4 動作選擇策略設計

訓練過程中，本文采用ε-貪婪策略進行動作選擇，通過引入隨機變量ε∈(0,1)，每次以概率ε進行探索，以概率1-ε進行利用，即每次在選擇動作時都生成隨機數randt，動作的選擇策略滿足

(4)

式中：St、At分別為t時刻智能體所處位置與所執行動作；A為動作空間；Qt(·)為t時刻執行動作后轉移到新狀態的Q值；A(R>0)表示執行動作后即時回報大于0的動作集合。

1.1.5Q值更新方式定義

根據Q學習算法的定義，經驗矩陣中Q值更新規則滿足

(5)

式中：α∈(0,1)為學習效率，影響學習收斂的快慢；γ∈(0,1)為衰減值，某兩個狀態相隔的時間越長，則后一狀態對前一狀態的影響越小。

1.2 基于Q學習的航跡規劃方法

基于Q學習的單無人機航跡規劃方法按照以下步驟進行。

步驟1初始化環境、無人機的初始位置與期望位置，初始化經驗矩陣Qtable、學習效率α，衰減值γ，最大迭代步數tmax，最大幕數episodemax，ε-貪婪策略參數ε。

步驟2初始化無人機的初始位置為當前狀態。

步驟3生成隨機數randt，判斷randt是否大于ε，是則選擇當前狀態下Q值最大的動作執行，否則隨機選擇動作執行。

步驟4執行動作后無人機轉移到新的狀態，根據式(3)計算即時回報，根據式(5)對經驗矩陣Qtable進行更新。

步驟5判斷無人機是否到達期望位置或達到最大迭代步數tmax，若未到達且當前步數小于最大迭代步數，則令新的狀態為當前狀態并返回步驟3，否則執行步驟6。

步驟6判斷是否到達最大幕數episodemax，若未到達則返回步驟2，否則終止計算并輸出Qtable。

當已訓練得到完備的經驗矩陣Qtable后，此Qtable表示了在每個狀態下無人機采用4個動作的優劣性，Q值越大的動作越快趨向目標。因此，可直接基于此Q-table獲得無人機從任一起始點出發到達目標位置的最優航跡。為保證航跡的最優性，在基于訓練后的Q-table選擇動作時采用貪婪策略。

2 基于Q學習的多無人機協同航跡規劃方法

2.1 考慮時間協同的協同航跡規劃算法

基于1.2節可得到能夠避免障礙物且航跡最短的單無人機航跡。對于實現圍捕目標目的的多無人機協同航跡規劃問題，其在單無人機航跡規劃的基礎上，增加了各無人機飛行時間相等的約束。

假設對N架無人機進行協同航跡規劃，由于本文中無人機的速度為常值且相等，飛行時間相同問題就轉化為多無人機航跡長度相等的問題。根據第1節內容，可分別獲得各無人機到期望位置的最優航跡長度P1,P2,…,PN，考慮協同航程Pc的最優性與可行性，選擇最長的航跡長度作為協同航程，即

Pc=max (P1,P2,…,PN)

(6)

對于航跡長度小于Pc的無人機，需要對其航跡進行擴展，即無人機需要繞飛。對于無人機i，在飛行過程中的動作選取策略調整為

(7)

Pi=Pi0t+Pite,i=1,2,…,N

(8)

式中：Pi0t為無人機飛到當前位置經過的航跡；Pite為從t+1步起，在當前狀態下根據經驗矩陣Qtable選擇最優航跡到達目標所需航跡長度。由于每個狀態Q值最大的動作對應的航跡是長度最短的航跡，需要繞飛時就不能選取Q值最大的動作，而是在其他可行動作中隨機選取。

假設針對同一環境下單無人機的航跡規劃經驗矩陣已訓練完畢，則滿足時間協同的多無人機航跡規劃求解步驟如下：

步驟1初始化各無人機的初始位置、期望位置、當前狀態，根據當前狀態，按照式(6)選擇航跡長度最長的作為協同航跡Pc。

步驟2根據當前狀態，按照已訓練好的經驗矩陣Qtable，計算各無人機到達期望位置的航跡長度Pi(i=1,2,…,N)。

步驟3判斷各無人機航跡長度Pi是否與Pc相等，若相等則執行步驟4，否則各無人機按照式(7)進行動作選擇，返回步驟2，重新計算各無人機到達期望位置的航跡長度。

步驟4各無人機根據貪婪算法選擇動作執行，并進行狀態轉移，執行步驟5。

步驟5判斷各無人機是否到達期望位置，若未到達則返回步驟4，否則終止計算，并輸出各無人機的協同航跡。

2.2 碰撞避免策略設計

多無人機按照2.1節規劃的航跡飛行時可能發生碰撞，因此需要在2.1節算法中加入碰撞檢測模塊，并針對發生碰撞的航跡進行局部重規劃，其余未發生碰撞的航跡保持不變。本文設置從發生碰撞時刻的前Sback步開始進行局部重規劃，并將該時刻所處狀態作為局部重規劃的初始位置，將原航跡組中碰撞結束后的下一時刻狀態作為無人機局部重規劃的期望位置。局部環境的選取如圖3所示。

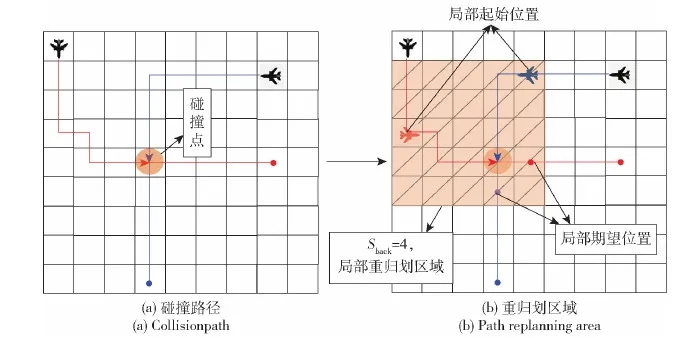
圖3 多無人機局部航跡重規劃Fig.3 Partial path replanning for multiple UAVs

圖3中，兩無人機基于2.1節算法得到的航跡存在碰撞點(見圖3(a))，因此需要對局部航跡進行重規劃。若令后退參數Sback=4，則圖3右圖中紅色無人機和藍色無人機分別為紅色航跡和藍色航跡無人機從碰撞點后退4步后的位置。作為兩個無人機局部重規劃的初始位置，紅色圓點和藍色圓點分別為發生碰撞后兩個無人機的下一個非碰撞狀態，作為兩無人機的期望位置，將包含上述初始位置、期望位置的矩形區域作為局部重規劃區域。需要注意的是，在局部規劃時，通常在某個狀態會有大于1個的最優動作，為了不改變重規劃前航跡的長度，應選擇重規劃路徑長度為4的動作。若沒有這種動作，則重規劃后的航跡長度變化，可增大后退參數取值，在更大范圍內尋找協同路徑。

定義局部重規劃區域的回報函數為

(9)

式中：a、b、c為大于0的常數，-a引導無人機避開障礙物，-b引導無人機避免相互碰撞，c引導無人機向期望位置飛行。

為避免隨著無人機個數增多導致狀態、動作空間指數級上升，本文使用DQN方法對局部碰撞區域進行重規劃，通過構建神經網絡模擬Q-table輸出，從而解決Q-table維數過高、收斂難度大的問題。DQN算法以神經網絡作為載體，通過神經網絡的輸出值模擬Q-table輸出的Q值，可表示為

f(S,A,w)=Q*(S,A)

(10)

式中：S為無人機狀態；A為所選動作；w為神經網絡的權重參數；Q*(S，A)為S狀態下執行A動作的Q值。

由于采用多無人機進行協同航跡規劃，輸入項為多架無人機的動作與狀態，輸出為各無人機執行相應動作的聯合Q值。若局部空間有Na架無人機發生碰撞，每架無人機有上、下、左、右4個可選動作，則神經網絡模型如圖4所示。

圖4 局部重規劃的神經網絡模型Fig.4 Neural network model of partial path replanning

圖4中，神經網絡有3Na個輸入，分別為Na架無人機的x軸坐標(柵格編號)、y軸坐標及所選動作，輸出為神經網絡模擬經驗矩陣的Q值。

為使神經網絡應用在Q學習算法中保持穩定，建立雙層網絡結構，包括訓練網絡Qnet(St+1,a,w)與目標網絡Qtarget(St+1,a,w-)，兩個網絡的結構相同、參數不同，w-為Qnet中網絡參數w的延遲更新值。其中，訓練網絡Qnet用于選擇動作，更新模型參數，目標網絡Qtarget用于計算目標Q值。Q值計算公式為

(11)

式中：R為式(9)所示聯合動作的即時回報；γ∈(0,1)為衰減值；Q為訓練網絡Qnet(St+1,a,w)的期望輸出。

為實現神經網絡對Q-table的擬合，根據期望輸出與實際輸出求解損失函數值，進而對網絡Qnet進行更新，損失函數[19]的求解公式為

(12)

每間隔一段時間，拷貝Qnet到Qtarget，進而降低目標Q值和當前的Q值相關性。

當訓練達到局部重規劃的最大訓練幕數時，網絡訓練終止。各飛行器從局部初始位置開始，采用Qnet計算不同狀態、動作下的Q值，選擇Q值最大的動作執行，直至各飛行器到達期望位置，即可獲得局部重規劃的路徑。需要說明的是，如果局部調整范圍選得大，則需要重新規劃的航跡長度較長，求解速度就會比較低；如果局部范圍選得小，則可調整的范圍較小，可能無法找到成功避免碰撞的航跡組，因此需根據戰場情況合理設置局部區域的大小。

2.3 存在突然發現的障礙物的規劃方法設計

無人機實際作戰時的戰場情況與離線訓練時的戰場情況存在差異，可能實際戰場中的某些障礙物事先并未被探明，但無人機在實際飛行時必須要躲避此未知障礙物。實際作戰時，無人機的探測范圍是有限的，不妨設障礙物位于Lob×Lob的柵格區域中心，當無人機進入此區域時，可探測到位于區域中心的障礙物，障礙物區域如圖5所示(見圖中Lob=5)。

圖5 未探明障礙物區域Fig.5 Unexplored obstacle area

參考人工勢場理論思想，當無人機距離障礙物越近時其所受斥力越大，無人機趨于遠離障礙物的方向飛行。在Q學習理論中，經驗矩陣Qtable也反映了無人機趨向目標的快慢程度，在同一狀態下Q值越大的動作到達目標所需步數越少。因此，當目標位于柵格區域的中心時，Q值越大則“引力”越大，越快趨向目標，當障礙物位于柵格區域的中心時，可在原有“引力”基礎上取負值，表示無人機所受“斥力”，Q值越小則需越快遠離目標。

針對圖5的障礙物區域，將障礙物位置設為目標，由于Q-table具有全局性，隨機選取區域內一點作為無人機初始位置，并采用第1節方法得到障礙物區域內已收斂的經驗矩陣Q1。當區域中心位置為障礙物時，障礙物區域產生斥力，因此令障礙物模型的Q-table求解公式為

Qobstacle=-kobQ1

(13)

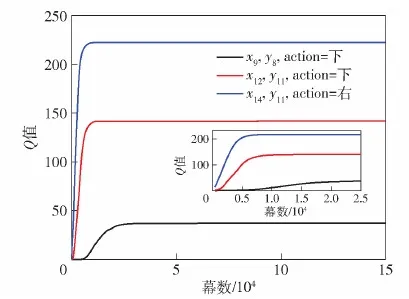
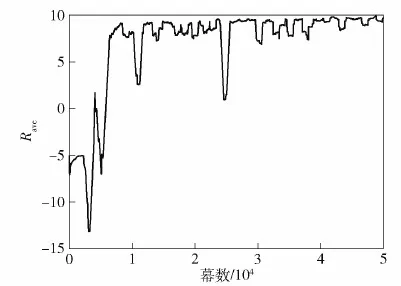
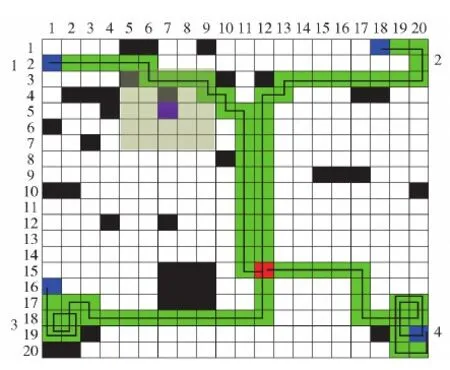
式中：kob為縮放系數，0

當無人機飛行過程中發現未探明障礙物時，在原有環境模型中疊加障礙物后的模型，如圖6所示。

圖6 疊加未探明障礙物后的戰場模型Fig.6 Battlefield model with unexplored obstacle

圖6中，淺綠色區域為未探明障礙物區域，區域中間紫色方格為障礙物所在位置，當無人機飛入淺綠色區域內時，即可探測到障礙物，此時經驗矩陣將在原有Q-table中的對應狀態及動作上疊加障礙物矩陣Qobstacle中的Q值，即

Qnew(S,A)=Q(S,A)+Qobstacle(S′,A)

(14)

式中：Qnew(S,A)為疊加障礙物矩陣后的Q值；S′為狀態S在局部區域內相對應的狀態。

2.4 多無人機協同航跡規劃算法流程

綜合考慮時間協同、避撞、存在未探明障礙物的情況，多無人機協同航跡規劃步驟如下。

步驟1初始化各無人機的初始位置、期望位置、環境，根據當前狀態按照式(6)選擇航跡長度最長的作為協同航跡Pc，執行步驟2。

步驟2根據Qtable計算各無人機到達期望位置的航跡長度Pi(i=1,2,…,N)。

步驟3判斷各無人機航跡長度Pi是否與Pc相等，若相等則按照貪婪策略選擇動作，否則各無人機按照式(7)進行動作選擇，轉移到新的狀態，執行步驟4。

步驟4判斷各無人機是否到達期望位置，若到達則執行步驟6，否則執行步驟5。

步驟5判斷各無人機是否發現先前未探明的障礙物，若是則在Q-table基礎上疊加未探明障礙物矩陣并返回步驟2，否則直接返回步驟2。

步驟6判斷各無人機是否存在碰撞，若是則對局部區域進行重規劃，否則執行步驟7。

步驟7輸出滿足時間協同與碰撞避免的協同航跡組。

3 仿真試驗

3.1 飛行時間協同航跡規劃方法仿真分析

假設有4架性能相同的無人機，無人機速度v=100 m/s，最大法向加速度azmax=20 m/s2，則最小轉彎半徑Rm=500 m。戰場環境為L×W=40 000 m×40 000 m的正方形區域，根據式(2)可得N=400，因此本文仿真算例將戰場離散化為20×20的柵格區域，行和列的編號從上至下、從左至右依次是1～20，(x,y)表示所在的行和列。為了使戰場柵格位置與經驗矩陣Qtable的狀態對應，將400個戰場柵格從左至右、從上至下依次編號為狀態1～400。單無人機的初始位置為(2，2)，期望位置為(15，12)。Q學習算法模型的參數設計為學習效率α=0.01，衰減值γ=0.8，最大迭代步數tmax=800，最大幕數episodemax=150 000，ε-貪婪策略參數ε=0.2。回報函數的設置為

進一步設置障礙物，得到戰場示意圖如圖7所示。

圖7 仿真算例戰場模型Fig.7 A simulation example of battlefield model

按照1.2節訓練步驟對此模型進行訓練，訓練后得到完備的經驗矩陣Qtable。以位置坐標分別為(8，9)、(12，11)動作為“下”的對應Q值Q168，2、Q231，2，以及位置坐標為(14，11)動作為“右”的對應Q值Q271，4為例，圖8顯示了3個Q值隨幕數增大的取值變化曲線。

圖8 部分Q值變化曲線Fig.8 Part of Q value variation curves

由圖8中可見，3個狀態、動作對應的Q值均收斂到穩定值，但不同位置Q值收斂速度不同，Q271，4在7 250幕收斂，Q231，2在13 321幕收斂，Q168，2在39 623幕收斂。根據Q值迭代公式(式(11))可知，通常離期望位置近的狀態收斂得快，因為Q值的更新依賴于下一時刻的狀態，下一時刻狀態收斂后當前狀態才可收斂，而離期望位置遠的狀態由于前期探索次數較少，往往收斂得較慢。因此，Q271，4收斂最快，Q168，2收斂最慢，而Q231，2介于二者之間。通過對多個局部Q值進行驗證可知，經過50 000幕訓練后Q-table已全局收斂，即已得到完備的經驗矩陣，可用于求解協同航跡，所需訓練時間為1 283.442 s。

假設各無人機初始位置和期望位置所對應的柵格編號如表1所示。為實現各無人機對目標的圍捕，期望位置設為(15，12)。

表1 無人機相關參數Table 1 Parameters of UAVs

禁飛區定義與圖7一致。根據2.1節滿足時間協同的協同航跡解算方法，得到步數相等的協同航跡如圖9、圖10所示。需要說明的是，根據訓練得到的Q-table得到無人機1、2、3、4的最優航跡步數分別為24、20、14和12，因此選擇24為協同航程；由于存在Q值相同的最優動作，在選取動作時從最優動作中隨機選取，會出現滿足最短協同航程的多組最優航跡，本文算例僅列出兩種滿足時間協同的協同航跡。

圖9 滿足時間協同的協同航跡1Fig.9 Time-coordinated path 1

圖10 滿足時間協同的協同航跡2Fig.10 Time-coordinated path 2

圖9和圖10中各無人機都能以最短協同航程24步到達期望位置。由于無人機2、3、4到達目標所需的最短航跡小于24步，通過繞行的方式實現時間協同，其中無人機3、4離目標距離較近，因此需要進行較長時間的繞行后再向目標飛行。但由于在動作選擇策略中設定了選取非最優動作時盡量和上一步的動作相同，圖9和圖10中的繞行軌跡在一定程度上相對平直。從圖9和圖10中可見，雖然各無人機能夠以相同的協同航程到達目標，但是由于未考慮無人機的碰撞避免問題，無人機1、2發生碰撞。

A*算法是一種典型的啟發式搜索算法，可在有效時間內搜索到滿足要求的可行航跡，近年來也被應用于協同航跡規劃問題，此處給出采用文獻[20]中的A*算法對本仿真算例進行時間協同航跡規劃問題求解的結果，如圖11所示。

圖11 基于A*算法的協同航跡Fig.11 Time-coordinated paths based on A* algorithm

由圖11中可見，A*算法雖然實現了時間協同，但是與Q學習算法相比，局部碰撞區域增大，處理難度增加，這是因為在Q學習算法中，步數少的無人機在開始飛行的動作選擇初期選擇非最優動作實現繞行直至期望步數與協同航程相同，因此無人機在初始位置附近盤旋，當滿足協同航程約束時朝目標飛行，而A*算法需要綜合考慮代價函數中趨于目標與趨于時間協同的兩方面因素，無法對繞行時刻進行約束，導致無人機在接近目標時仍處在繞行階段，由于各無人機的期望位置相同，碰撞概率增大。

基于A*算法和基于本文Q學習算法的協同航跡規劃方法在計算耗時上有較大的差別。基于A*的方法由于在過程中要進行不斷的搜索，而且搜索空間隨搜索維度呈指數級增長，耗時較長。相比而言，本文基于Q學習的方法僅需根據離線訓練好的Q-table按照預設的策略尋找軌跡即可，因此求解速率較快。分別進行5次仿真，A*算法與Q學習算法協同航跡規劃所需時間如表2所示。仿真結果表明，Q學習算法在求解協同航跡規劃問題時耗時較短，求解效率更高，平均提高63.8%。

表2 Q學習算法與A*算法性能對比Table 2 Performance comparison between the Q-learning and A* algorithms

當飛行器間存在碰撞或考慮戰場環境中事先未探明障礙物時，A*算法都需要根據當前場景進行重新規劃，例如戰場中有未探明障礙物時，需要在新的戰場環境下從目前點到終點重新進行規劃計算，相對本文中疊加Q表的方法，將花費更多的時間。因此，以下不再進行兩種算法的對比。

3.2 碰撞避免策略仿真分析

對圖9中無人機3、4進行局部重規劃，局部區域有兩架無人機發生碰撞，令Sback=5，Na=2。從碰撞點后退5步后的位置，作為兩個無人機局部重規劃的初始位置，由于兩無人機的期望位置相同，設到達期望位置前一時刻的非碰撞位置作為局部期望位置，得到6×3的局部重規劃區域如圖12所示。

圖12 局部重規劃區域Fig.12 Partial path replanning area

圖12中藍色區域為兩個無人機的初始位置，紅色區域為期望位置，根據局部區域的新編號，得到局部區域內的無人機初始位置、終點期望位置如表3所示。

表3 局部區域無人機3、4的初始位置、期望位置Table 3 Starting position and expected position of UAV 3 and 4 in the partial area

獎勵函數設置為

設局部重規劃的神經網絡含有兩個隱藏層，每層80個神經元，輸入為兩架無人機的x軸坐標、y軸坐標以及各無人機的動作，輸出為擬合的Q值，記憶矩陣最大容納量為8 000，定義平均回報Rave為1 000個回合內總回報的平均值，平均回報曲線如圖13所示。

圖13 平均回報函數曲線Fig.13 Average reward curve

由圖13可見，觀察期的回報波動較大，探索期隨著訓練次數增加算法的平均回報曲線呈現波動上升趨勢，當經過50 000幕時平均回報逐漸趨于穩定，此時網絡已訓練得較充分，可用于求解最優航跡。根據訓練網絡選擇Q值最大的動作進行狀態轉移，得到局部重規劃航跡如圖14所示。

圖14 局部重規劃示意圖Fig.14 Diagram of partial path replanning

由圖14可見，采用DQN算法可有效對局部航跡進行重規劃，將局部航跡替換到全局航跡中，即可獲得滿足時間協同與多無人機碰撞避免的最優航跡組。全局航跡圖如圖15所示。

圖15 協同航跡圖Fig.15 Diagram of cooperative path

3.3 存在未知障礙物的規劃方法仿真分析

設置未探明的障礙物位置為(5，7)，得到戰場示意圖如圖16所示。

圖16 存在未探明障礙物戰場的仿真算例Fig.16 Battlefield model with unexplored obstacle for simulation

圖16中，紫色柵格為未探明障礙物位置，假設無人機飛入淺綠色區域內，則可探測到位于中心的障礙物。根據2.3節算法進行未探明障礙物的躲避，若無人機進入淺綠色區域，則在原有Q-table中疊加一個障礙物矩陣。取kob=1/|Qob(S，A)|max=0.003 6，則疊加障礙物矩陣與未疊加障礙物矩陣的局部Q-table如表4、表5所示。

對比表4、表5可知，僅對障礙物區域內(state48、state69)的數值進行了疊加變換，而障礙物區域外(state1、state70)的數值未改變。

采用表4中的未疊加障礙矩陣的Q-table直接進行航跡規劃時，得到的一種最優航跡組如圖17所示。

表4 疊加前局部經驗矩陣取值Table 4 Partial Q-table before superposition

表5 疊加后局部經驗矩陣取值Table 5 Partial Q-table after superposition

圖17 存在未探明障礙物的協同航跡1Fig.17 Cooperative path 1 with unexplored obstacle

圖17中各架無人機滿足時間協同，但是由于存在位于(5，7)的先前未探明障礙物，無人機1將會與障礙物發生碰撞，進而導致圍捕任務失敗。

采用表5中疊加了障礙矩陣后的Q-table，假設探測到障礙物前各無人機的航跡與圖17所示航跡相同，則得到仿真結果如圖18所示。

圖18 存在未探明障礙物的協同航跡2Fig.18 Cooperative path 2 with unexplored obstacle

從圖18中可見，無人機1成功躲避了先前未探明的障礙物。根據表5所示，當無人機1位于State48(坐標(3，8))時，由于疊加了障礙物矩陣，動作“右”對應的Q值9.363 8大于動作“下”對應的Q值9.133 4，這是因為位置(4，8)比位置(3，9)更接近障礙物，按照最大Q值選取動作時無人機會轉移到State49，按此Q-table進行狀態轉移，直至轉移到障礙物區域邊緣，如表5所示state69(位置(4，9))的最大Q值對應動作為“右”，執行動作后無人機轉至state70(位置(4，10))，此狀態下疊加與未疊加障礙物矩陣的各個動作所對應的Q值相同，即障礙物區域外的Q-table數值未發生改變。因此，無人機1進入未探明障礙物區域后，在未探明障礙物的“斥力”以及期望位置的“引力”的雙重作用下，躲避障礙物的同時趨向目標飛行。經檢驗，所規劃的航跡中各飛行器未發生碰撞，因此無需對局部區域進行重規劃。

4 結論

本文設計了一種基于Q學習算法的協同航跡規劃方法，可以實現多無人機對目標的同時打擊。得出主要結論如下：

1)基于已有Q-table的多無人機滿足時間協同的航跡規劃方法，充分應用Q學習理論不依賴于初始狀態的特點，顯著提升了在線應用的求解效率。

2)基于DQN算法的局部航跡重規劃方法，避免了Q-table維度爆炸問題，有效降低了多無人機碰撞避免問題的求解難度。

3)通過與人工勢場法原理類比設計的針對未探明障礙物的臨時避碰策略，能夠應對在線應用過程中戰場環境與訓練模型存在差異的情況，顯著增加網絡的實用性。