巴特沃斯高通濾波器的優化設計與仿真實現

姚林杰，王耀斌，蔣 偉

（株洲宏達電子股份有限公司，湖南株洲 412011）

0 引言

濾波器是一種選頻裝置，可以使信號中特定的頻率成分通過，且極大地衰減其他頻率成分。利用濾波器的這種選頻作用，可以濾除干擾噪聲或進行頻譜分析［1-2］。濾波器可廣泛應用于工業、商業和機關團體的配電網中，在人們日常生活中有著不可替代的作用。

濾波器作為一個系統的重要元器件，它的優劣會影響著整個系統的功能和質量［3］。早期的濾波器主要是由無源元件電容、電感和電阻組成的濾波電路。自20 世紀60年代以來，隨著集成運放的發展，由集成運放、電容、電阻組成的有源濾波電路得到廣泛應用，相比于無源濾波電路，有源濾波電路有著不用電感、體積小、重量輕的優點，所以有源濾波器在幾十年間得到了快速發展［4］。

目前，相比于低通濾波器，高通濾波器的探討與研究較少。開關電容式專用濾波芯片等器件的出現使得高通濾波器的實際應用成為現實［6］。然而，由于其電路存在噪聲等因素，會對濾波器的濾波效果產生負面影響。因此，對RC有源高通濾波器進行優化設計的相關研究具有一定的工程應用價值［2］。

本文提出了一種四階RC 有源巴特沃斯高通濾波器的設計方法，該方法在確定電容和增益的基礎上先設計出二階高通濾波器，然后在此基礎上利用低通濾波器與高通濾波器之間的頻率轉換函數設計四階巴特沃斯高通濾波器。該設計方法不僅可以使二階濾波電路系統取得最佳阻尼系數，同時它的網絡元器件參數也較易選擇。基于該方法設計出的兩個四階巴特沃斯高通濾波器也具有良好的幅頻特性。

1 壓控電壓源式二階高通濾波電路的設計

常見的二階高通濾波電路主要有兩種形式，即無限增益多路反饋式和壓控電壓源式［7］。由于壓控電壓源式電路具有輸入阻抗較高且輸出阻抗較低的特性，同時所需的精密電阻、電容器件較少，對運放要求也低，故本文采用壓控電壓源式二階高通濾波電路作為高階高通濾波電路的基本單元。其電路原理如圖1 所示。

圖1 壓控電壓源式二階高通濾波電路

可得電路如圖2 所示。

圖2 Af＝2 時二階高通濾波系統電路圖

可得電路如圖3 所示。

圖3 Af＝2 時二階巴特沃斯高通濾波系統電路圖

基于所設計的二階巴特沃斯高通濾波器電路，利用Multisim14.0 電路仿真軟件和Origin 2019 繪圖軟件得到兩個二階RC 有源高通濾波器的歸一化幅頻特性曲線如圖4 所示。

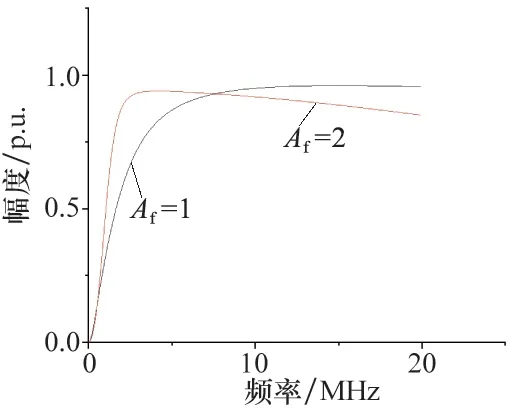
圖4 二階RC有源高通濾波器的歸一化幅頻特性曲線

觀察圖4 可以明顯發現相比Af＝2時的幅頻特性曲線，Af＝1時的幅頻特性曲線更為平坦，且隨著頻率的增加曲線較為穩定。

至此，已經完成Af不同的取值下的二階高通濾波電路的設計，接下來將設計高階巴特沃斯高通濾波器。

2 四階RC有源巴特沃斯高通濾波器的設計

根據逼近方法的不同，濾波器可以劃分為巴特沃斯（Butterworth）濾波器、貝塞爾（Bessel）濾波器、切比雪夫（Chebyshev）濾波器等類型［9］。其中，巴特沃斯濾波器最顯著的特點是在通頻帶內具有最為平坦的幅頻特性，且在過渡帶內具有單調下降的幅頻特性，因此，巴特沃斯得到了廣泛的應用［10］。本文基于巴特沃斯濾波器設計四階RC有源高通濾波器。

設計高通濾波器的方法一般是找到與設計指標相對應的低通濾波器的傳遞函數，然后通過低通濾波器與高通濾波器之間的頻率轉換求出高通濾波器的傳遞函數［8］。已知低通濾波器和高通濾波器之間的轉換公式如式（18）所示。

依據線性電路網絡理論，有源濾波器的輸入輸出不會因為級聯的原因而產生額外的干擾信號［2］。故可以將二階高通濾波電路進行級聯的方式獲得四階高通濾波電路［11］。

根據第1節所設計的二階高通濾波單元，可得當時四階高通濾波系統的電路，如圖5所示。

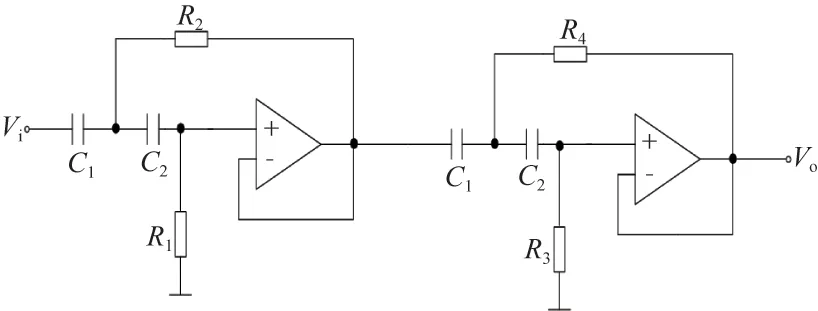
圖5 Af＝1時四階高通濾波系統電路圖

當Af＝1時四階高通濾波系統的電路如圖6所示。

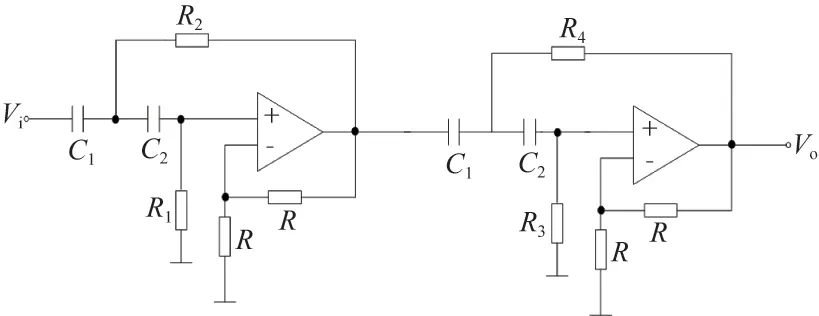
圖6 Af＝2時四階高通濾波系統電路圖

3 設計實例與仿真

本節將設計一個通帶截止頻率為100 kHz的四階RC有源巴特沃斯高通濾波器并開展仿真。

首先在理論上設計當Af＝1時的四階巴特沃斯高通濾波器，對兩個具有相同Af值的二階巴特沃斯高通濾波器進行級聯可以得到一個對應Af值的四階巴特沃斯高通濾波器［12］。由前面推導的歸一化的四階巴特沃斯高通濾波器的傳遞函數的公式，第一個二階巴特沃斯高通濾波器的傳遞函數為：

然后用Multisim14.0電路仿真軟件來仿真設計的四階巴特沃斯高通濾波器電路，仿真電路圖如圖7所示。

圖7 Af＝1 時四階巴特沃斯高通濾波器的仿真電路

同時利用Origin 2019軟件進行數據整理，然后可以得到歸一化幅頻特性曲線如圖8所示。

圖8 Af＝1 時四階巴特沃斯高通濾波器幅頻特性

同理設計當Af＝2 時的四階巴特沃斯高通濾波器，由兩個具有相同Af值的二階巴特沃斯高通濾波器進行級聯可以得到一個對應Af值的四階巴特沃斯高通濾波器［12］。由前面推導的歸一化的四階巴特沃斯高通濾波器的傳遞函數的公式，可以得到第一個二階巴特沃斯高通濾波器的傳遞函數為：

與前面所推導的傳遞函數相對應：

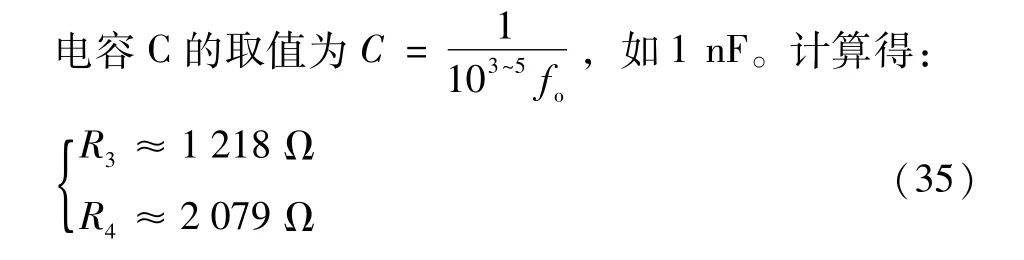
同樣地，用Multisim 14.0 電路仿真軟件來仿真設計的四階巴特沃斯高通濾波器電路，仿真電路圖如圖9所示。

圖9 Af＝1 時四階巴特沃斯高通濾波器的仿真電路

然后利用Origin 2019 軟件進行數據整理，可以得到歸一化幅頻特性曲線如圖10 所示。

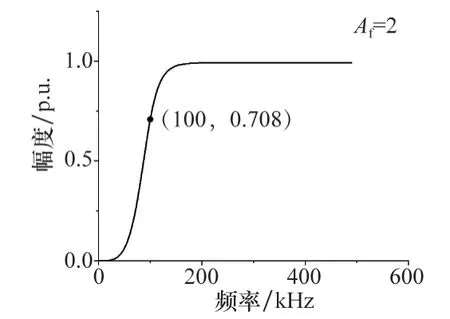
圖10 Af＝2時四階巴特沃斯高通濾波器幅頻特性

最后將設計的兩個四階巴特沃斯高通濾波器的幅頻特性曲線放在一起進行比較，如圖11 所示。

圖11 不同增益的四階巴特沃斯高通濾波器幅頻特性對比

觀察圖11，可以發現不同于圖4，這兩個四階RC有源巴特沃斯高通濾波器的幅頻特性曲線幾乎一致，不僅更加穩定，且都滿足設計要求，即在100 kHz 處幅度為0.707 p.u.左右［14］。仿真結果證明，同樣的設計方法，不同增益下的二階高通濾波器的幅頻特性曲線具有明顯差異，而本文設計的四階RC 有源巴特沃斯高通濾波器可以得到具有幾乎重合的幅頻特性曲線。相比之下，增益為1 時，使用的網絡元器件相對較少，設計相對更加簡單。

4 結束語

本文通過確定電容和增益的方式先設計二階高通濾波器，然后在二階高通濾波器的基礎上，利用低通濾波器與高通濾波器之間的頻率轉換函數算出四階巴特沃斯高通濾波器傳遞函數的表達式，提出可以通過將二階高通濾波電路進行級聯的方式獲得四階巴特沃斯高通濾波器。最后設計一個通帶截止頻率為100 kHz 的四階巴特沃斯高通濾波器并通過仿真實現。

本文方法計算簡單，網絡元器件的選擇方便快捷，并且最后的仿真結果顯示設計的四階RC 有源巴特沃斯高通濾波器的濾波特性都較好，都能滿足設計要求。