深度體悟，把握數學概念本質

黃肖慧

摘 要：在通過深度學習實現學生高階思維發展的教育背景下，本文以人教版教材“圓的認識”為例，依托APOS理論的支撐，在學情調查分析的基礎上，開展“具身體悟，驗證體悟，符號體悟，遷移體悟”四步走的教學實踐，引導學生在深度體悟中把握“圓”的概念本質，并進入到方法與策略、經驗與聯結的思維拓展層面，培養高階思維.

關鍵詞：體悟；思維；概念本質；圓

近期，筆者有幸加入廣東省“南方教研大講堂”活動的備課團隊，參與“圓的認識”一課的備課過程.“圓的認識”是“圖形與幾何”概念教學的經典課例，是從認識直線圖形向認識曲線圖形轉變的一次飛躍.本課依托杜賓斯基等人的APOS理論，遵循“感知概念—理解概念—描述概念—應用概念”的教學結構，從學生的認知起點出發，以深度體悟引領學生把握“圓”的概念本質，培養高階思維，打造深度學習課堂.

1?學情分析與課前思考

為把握學生學習的起點，備課團隊根據本課的教學目標，以問卷形式對相關知識進行了前測.

通過前測，發現大多數學生知道半徑、直徑，但能夠在圓中準確表示出來的只有10%左右；有超過一半的學生曾經用圓規畫過圓，但能準確畫指定大小的圓只有極少數.超過70%的學生提出：想研究圓的周長、面積，圓環面積，而“圓的特征”“圓的畫法”這些問題被關注度不高.在進一步的訪談中發現，大部分學生未能從數學思考層面來描述圓的本質屬性.

“圓的特征”“圓的畫法”這些問題，本質上都指向“圓是什么”.通過研究“圓的特征”“圓的畫法”可理解“圓是什么”，而理解了“圓是什么”，才能深刻領會“圓的特征”“圓的畫法”.因此本課主要分四步走，引領學生深度體悟，發展高階思維.

2?教學實踐

2.1?具身體悟：從操作到想象

圓與其它學習過的平面圖形相比，是與眾不同的.首先，圓是一個中心對稱的曲線圖形，圓上任意一點到圓心的距離都相等；其次，半徑、直徑作為圓的重要組成部分，是隱藏于圓的內部線段.這些都與其它直線平面圖形有著本質的區別.^［1］通過分析圓的概念內涵及其在平面圖形概念體系中的位置，本課創建“尋寶情境”，來幫助學生獲得“平面內與圓心距離相等的動點軌跡”的感性認知，在情境中洞察概念屬性.

【片段一】情境中感知圓

師：同學們，根據“寶物在距離小旗2米的草地表面”，你能說出寶物可能藏在哪嗎？

小組合作：用一個紅點代表小旗，在透明紙上把寶物的可能所在位置用點表示出來.教師展示作品，把各組作品堆疊在一起.

師：當這無數個點匯集在一起，想象一下，連起來會是一個什么圖形？你能用手在空中描出這個圖形嗎？

學生的認知依附于身體，而身體又存在于特定的環境中，創設情境是學生快速進入認知過程的有效途徑，它直接影響學習者的投入程度^［2］.動手描點，指尖動作參與概念建構，直觀形象地表達動點的抽象軌跡；想象補充，促使動點成圓在頭腦中生成；徒手繪圓，及時把頭腦中的圓具象化.

2.2?驗證體悟：從操作到推理

杜賓斯基的APOS理論認為，第二階段是概念的過程階段，是對“活動”進行思考，通過一定的抽象得出概念的特有性質.與引領學生經歷“活動”相比，啟發學生對“活動”的本身進行思考更為重要.關注獲得知識的策略，聚焦數學方法論，才能更深層次地發展學生思維，實現深度理解.

【片段二】驗證圓的特征

師：老師提供一些不同大小的圓形紙片，請折一折、畫一畫、量一量、想一想，探究圓到底有什么特征？

學生合作探究，集中反饋.

師：大小不同的圓，是不是都具備了這些特征？

你是怎么發現這些特征的？

……

師：如果不操作，你能聯系情境解釋以上特征的合理性嗎？

生：寶物距離小旗2米，在以小旗為圓心的2米距離畫點，這樣的點有無數個，這無數個點與小旗所在位置（圓心）連接，就形成了無數條半徑，它們都是2米長……

在探究圓的特征這一活動中，學生表現出不同的思維層次，相當一部分只關注“我發現了什么”這一問題.教師適時追問：“大小不同的圓，是不是都具備了這些特征？”這暗示學生通過找不同大小的圓，舉更多的例子來驗證.但是，停留在“舉更多的例子”也是不夠的，因為例子再多也只是同一思維層面上的單調重復.此時，教師再追問：“你是怎么發現這些特征的？”“如果不操作，你能聯系情境解釋以上特征的合理性嗎？”這是更高層次的引導，從關注“是什么”轉向關注“為什么”.思維從動手驗證的感性水平上升到推理證明的理性水平.誠然，前者指向知識的陳述，后者指向策略的反思，對學生而言后者是更具成長價值的學習.^［3］

2.3?符號體悟：從操作到抽象

杜賓斯基的APOS理論提出：第三階段是對象階段，是對“活動”與“過程”的升華，將抽象出的概念賦予其形式化的定義及符號，成為一個具體的“對象”.

雖然小學教材沒有正式提出圓的概念，但是把圓的概念符號化還是必不可少的.進入第三階段，要把情境中的圓、學具圓片抽象成“對象”，落到紙面上，讓學生體悟符號的生成.^［4］

【片段三】對比中畫圓

先讓學生用圓規在紙上畫半徑為2厘米的圓.

師：草地上半徑2米的大圓，還能用圓規畫嗎？

師：紙上畫圓與草地上畫圓，方法有什么不同？

為什么沒有圓規也畫出了圓呢？

生：確定了圓心和圓心到圓上的距離，就能畫出圓.

“兩種畫圓方法有什么不同？”，這是同中求異，再次引證圓心決定位置，半徑決定大小；“為什么沒有圓規也畫出了圓？”，這是異中求同，引導發現不同工具發揮的相同作用，感受“一中同長”.思考直達概念的核心，逐步實現圓的符號化.

2.4?遷移體悟：從理解到運用

杜賓斯基等人認為，概念學習的第四階段是運用，是概念進一步的理解、揭示和實例化，最終要形成綜合的心理圖式.本課的練習環節嘗試從概念理解過渡到概念應用，催生聯結的思維方式和認知方式.

【片段四】練習中內化圓

練習一：

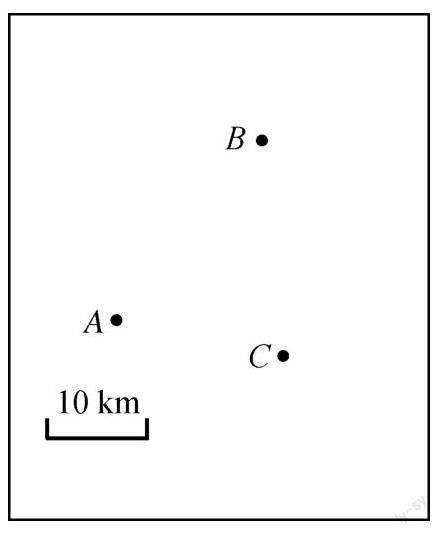
地震局預測A地于14：23左右將發生6—7級地震，波及范圍為20千米.

（地震小常識：地震波在地面的波及范圍是一個以震中為圓心的圓）

（1） 在圖中畫出以A地為震中的危險區域；

（2） 判斷B、C兩地是否在危險區域內.

練習二：

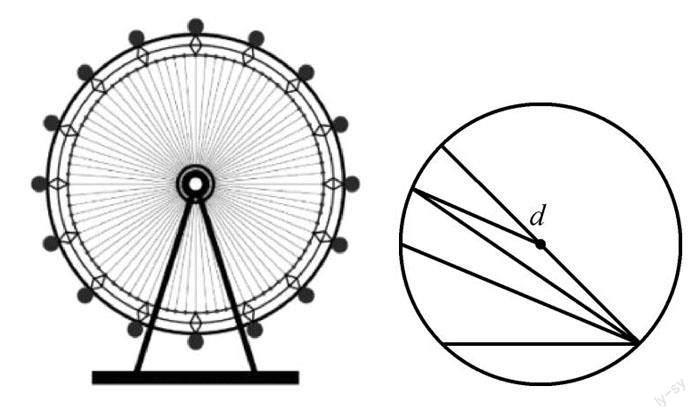
師：公園里有一個摩天輪，如果兩個人想坐在摩天輪距離最遠的兩個座位上，要怎么坐才可以呢？

練習三：拓展研究

尋寶活動中，如果信息改為：“寶物藏在距離小旗2米的地方”，猜想一下，寶物所在位置的軌跡，會是一個什么形狀？

練習一創設地震應用情境，進一步揭示圓的本質特征，使圓的應用實例化.練習二創設摩天輪的應用背景，建立圓與其它平面圖形之間的知識聯結，啟發學生對平面圖形中線段之間的邏輯關系進行梳理，建立平面圖形之間的橫向聯系.練習三是對概念內涵、外延進行擴大，獲得圓與球體概念的邏輯聯結，從縱向上初步建立曲線圖形概念體系內部之間的聯系.

綜上，概念學習是不斷構建活動、對象、圖式的過程.經歷感知、內化和概括、復述和反思活動，在深度體悟中把握“圓”的概念本質，并進入到方法與策略、經驗與聯結的思維拓展層面，方能培養高階思維.

參考文獻：

［1］ 趙元中.用“行”撬動深度的“知”——“圓的認識”教學實踐與思考［J］.小學數學教育，2021（10）：70-72.

［2］ 侯凱瑩.小學數學具身教學設計研究——以“圖形與幾何”為例［D］.山西大學，2020.

［3］ 姚進.小學數學中“圓的認識”的教學設計研究——基于APOS理論［D］.揚州大學，2016.

［4］ 陳江輝.關于“圓的認識”教學的再思考［J］.小學數學教師，2018（2）：43-47.