核心素養視域下數學隱性課程資源的開發

杭毅成 高峰官

摘 要：新課標確立了核心素養導向的課程目標，注重對學生數學思維的培養.隱性課程資源是知識背后有利于課程實施的深層次元素所構成的集合，有利于培養學生的數學關鍵能力、品格和價值觀，是發展核心素養的有效手段.本文以“勾股定理的簡單應用”為例，立足于數學核心素養，深入挖掘隱性課程資源，引導學生對知識進行深入探索，獲得實踐經驗，發展數學思維.

關鍵詞：數學核心素養;隱性課程資源;勾股定理的簡單應用

隨著《義務教育數學課程標準（2022版）》的頒布，培養初中生的數學核心素養提上了新的高度.從發展的角度來看，數學核心素養既是對“四基”和“四能”的整合與細化，又進一步發揮了數學的育人價值，而如何在教學中落實核心素養是亟待解決的問題.數學課程資源作為教師教與學中運用到的各種資源，關系到整個教學的實施，其中數學隱性課程資源主要包括數學知識的過程、邏輯、背景、文化等元素，這些元素與核心素養所提倡的啟發學生用數學的思維思考，獲得必備的品格不謀而合.因此，需要進一步開發數學隱性課程資源，逐步由原來的知識教育為核心轉向以培養學生素養為核心.

1?基本概念及其特征

數學核心素養主要是培養學生會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實現實世界，其中初中數學核心素養更加側重對概念的理解.

在國內，《義務教育數學課程標準（2011版）》中出現了數學課程資源的概念.喻平教授進一步將數學課程資源分為外顯性資源和內隱性資源^［1］，外顯性資源大多以靜態的數學知識為主，而內隱性資源則是知識背后深層次元素構成的集合，例如：探索過程、數學思想、歷史文化等.

充分利用隱性課程資源，創造利于學生學習的教學內容，引導學生經歷探索的過程，獲得實踐的經驗，逐步形成數學思維，促進學生核心素養的發展.因此，挖掘隱性課程資源，有助于踐行新課標理念.

2?數學課程資源運用現狀

數學教師在課程資源的運用上注重外顯性資源，能在認真閱讀教材的基礎上，把握好教學的重難點，傳授書本上的知識點，訓練解題技能.但是很少有教師真正注重知識的探索與生成過程，缺乏挖掘基于數學教材的隱性資源，忽視學生核心素養的培育.因此，開發數學課程隱性資源是十分有必要，有助于提升數學課堂的品質，促進教師專業化發展和教學水平，最終讓學生在數學上獲得良好發展.

3?教學設計

筆者以開設的公開課“勾股定理的簡單應用”為例，詳細談一談如何在課堂中充分利用數學課程的隱性資源，發展學生數學核心素養.

3.1?背景分析

本節課是八上第三章的第三節內容，主要涉及運用勾股定理及其逆定理來解決一些簡單的實際問題.本課內容基于之前所學習的勾股定理和直角三角形的判定定理，發展學生的數學建模能力和應用意識，滲透“數形結合”“轉化”等思想.

學生在七年級已經對數學知識與實際應用的結合有了初步認識，為本課的學習打下了基礎.但是部分學生未充分認識到勾股定理及其逆定理的區別和聯系，仍缺乏分析問題、抽象出數學模型和解決問題的能力.

3.2?教學目標

（1） 經歷運用勾股定理和逆定理解決實際問題的過程，培養發現問題、分析問題和解決問題的能力.

（2） 經歷運用數形結合、轉化、方程的方法解決問題的過程，形成模型觀念，增強應用意識.

3.3?教學重難點

（1） 運用勾股定理及其逆定理解決實際問題；

（2） 運用數形結合、轉化、方程的方法解決問題.

3.4?教學流程

3.4.1?復習回顧

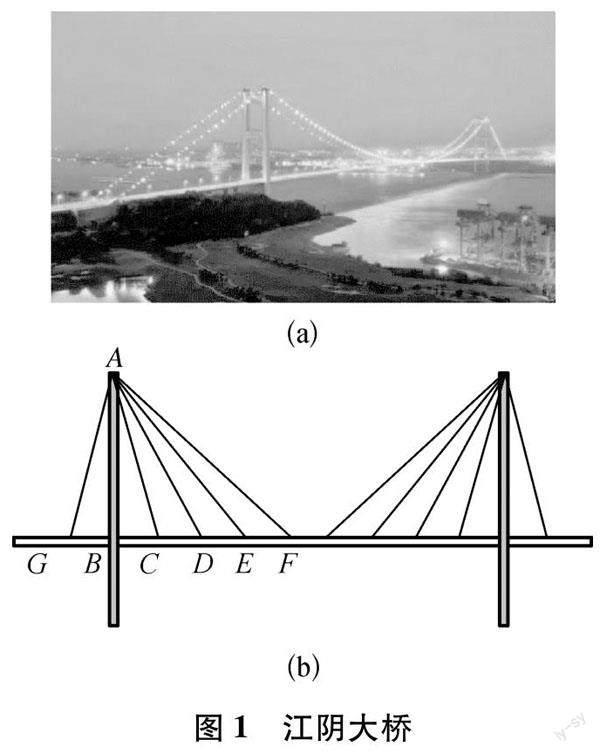
問題1：“一橋飛架南北，天塹變通途！”假期出游時往往會經過江陰大橋（如圖1所示）

（1） 觀察圖1（a），你能從中發現什么幾何圖形？

（2） 已知橋面以上索塔AB的高，怎樣計算AC、AD、AE、AF、AG的長.

（3） 工人檢修橋梁，已知索塔AB、橋面BC與拉索AC的長度，如何檢查索塔是否垂直于橋面？

設計意圖：依托江陰大橋這一實際背景，以真實問題為載體，引導學生回顧復習.

3.4.2?探索一、“折竹”問題

首先介紹《九章算術》作為古代算經之首，有著深厚的歷史底蘊，激發學生的民族自豪感和文化自信，進而引出“折竹問題”.

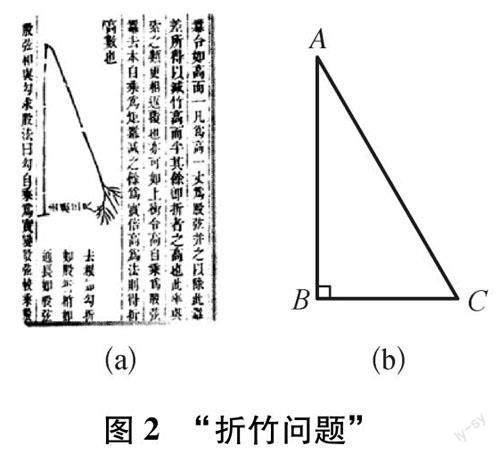
問題2：如圖2（a）所示九章算術中的“折竹”問題：今有竹高一丈，末折抵地，去根三尺，問折者高幾何？其大意是有一根竹子原高1丈（1丈＝10尺），中部有一處折斷，竹梢觸地面處離竹根3尺，試問折斷處離地面多高？

設計意圖：通過“折竹”問題來引導學生根據具體問題情境，抽象出幾何模型，使用方程思想來解決實際問題，激發學生的文化自信.

3.4.3?探索二、草坪問題

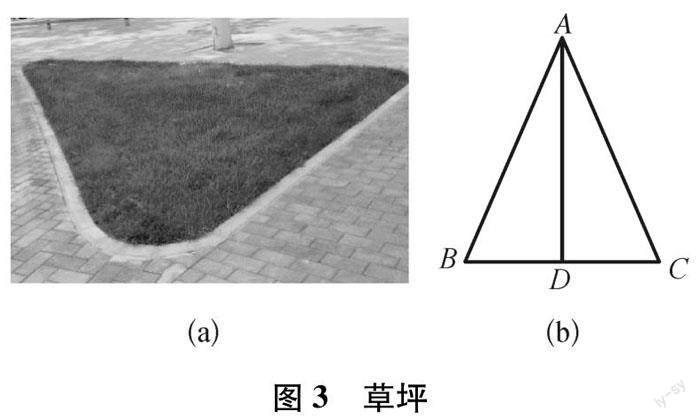
問題3：校園內有一個三角形草坪△ABC（如圖3所示） ，AD是△ABC的中線，AD=24dm，AB=26dm，BC=20dm.求AC的長.

變式1：如圖4所示，校園內有一四邊形草坪，∠A=90°，已知AD=12dm，AB=16dm，DC=15dm， BC=25dm，求四邊形ABCD的面積.

〖KH-1〗變式2：如圖5所示，校園內有一三角形草坪，已知AC=15dm，BC=14dm，AB=13dm，求△ABC的面積.

最后提出一個開放性問題：設計一個新的草坪形狀，要求可以利用勾股定理或逆定理求解草坪面積，看誰設計的草坪最漂亮！

設計意圖：以轉化思想為主線，通過解決一系列的草坪問題，滲透一題多解，體現問題設計的變化性、開放性，培養學生的創造力.

3.4.4?探索三、最短路徑

問題4：“白日登山望烽火，黃昏飲馬傍交河”是唐朝詩人李欣所作的詩句，其中蘊含著“將軍飲馬問題”.

如圖6所示，若詩中將軍從A點出發，走到河邊飲馬后再到B點宿營.已知點A、B到河邊的距離分別為2km和3km，點A和B間的水平距離為12km，請問怎樣走才能使總路程最短，最短為多少？

設計意圖：古代背景與現實背景相結合，設計一系列“最短路徑”問題，滲透數形結合和轉化思想，培育學生興趣，發展學生的應用意識.

3.4.5?總結提升

（1） 你是如何運用勾股定理及其逆定理解決實際問題的？

（2） 蘊含了什么數學思想？

（3） 結合之前學習的一元一次方程和一元一次不等式在生活中的應用，談一談如何將數學應用于生活.

設計意圖：通過知識與技能、數學思想以及知識之間的前后聯系這三個層面來引導學生進行總結，既回顧了本節課的內容，又從整體的角度把握知識的脈絡與研究方法.

4?教學反思

新課標下的數學教學著眼于培養學生的“三會”，這就要求教學不能局限于書本，要充分運用數學課程的隱性資源，著眼于培養學生的數學思維能力和創造力，充分發揮數學教學的育人功能.在數學核心素養視域下，抓住以下三方面，發展學生的核心素養：

4.1?了解背景，激發興趣

數學教學的背景分為知識背景和學生背景.數學知識不是憑空產生的，它有著豐富的現實和歷史意義，“勾股定理”作為幾何的基本定理，體現的“形數統一”思想對科學創新有著重要意義.在實際生活中，它在屋頂構造、橋梁設計等方面有著重要應用.從學生角度看，初二的學生有一定的幾何基礎和推理能力，但綜合運用能力較弱，要在課堂中逐步引導，以實際情境促進學生數學能力的發展.

在了解教學背景的前提下，將感性和理性相結合，充分融入文化元素，融入數學家們的事跡，在課堂中滲透堅持不懈、勇敢探索等精神，激發學生的學習興趣，增強文化自信.

4.2?經歷過程，發展思維

數學知識是相對真理，它產生于問題，隨著時代的變遷不斷發展變化，是一個過程，所以在課堂中用重視過程，積累學習經驗，發展數學思維.本課通過數學問題引導學生主動回憶之前學習的勾股定理及其逆定理，但是此前并沒有將其運用到生活中，學生在解決實際問題中會遇到困難，找到知識的生長點，激起學生的探索欲.在經歷一系列探索的活動中，收獲研究數學的方法，發展學生思維，培養應用意識、創新意識.

4.3?單元視角，整體思維

數學知識不是割裂的個體，它是一個體系，單個的知識點與較多其他知識存在著關聯.從單元的角度來看，所教內容往往存在著明線與暗線，需要我們站在不同的角度來研究.以本課為例，它是勾股定理及其逆定理的運用，也為之后進一步學習幾何奠定基礎，在總結時，引導學生從單元視角來理解該知識點.此外，從知識關聯來看，它是數學在生活中的應用中的一課時；思想角度來看，它是初中“數形結合”這一暗線中的一課時，因此課堂中要做好引導，為之后進一步研究做鋪墊.

樹立整體思維，有利于學生健全個性，引導學生用數學的眼光看待問題，用數學的思維思考問題，促進數學知識的掌握和靈活運用.

參考文獻：

［1］ 喻平.論內隱性數學課程資源［J］.中國教育學刊，2013（7）：59-63.

［2］ 中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022.

［3］ 高峰官，張珉.挖掘教材資源價值，激活核心素養——從一節課說數學隱性課程資源的開發和利用［J］.中學數學，2020（18）：11-12+28.

［4］?蔣茵.提升數學核心素養的有效途徑：與隱性知識深度對話——以基本不等式為例［J］.上海中學數學，2018（11）：32-35.

基金項目：江蘇省“十三五”教育科學規劃課題“初中數學隱性課程資源開發利用的實踐研究”（編號：E-c/2016/12）.