從一道數學試題的命制過程分析數學核心素養的考查方法

王志剛+阮飛

[摘 要] 數學評價必將從“能力立意”轉變為“素養立意”. 怎樣在試題命制過程中滲透數學核心素養，怎樣用核心素養的觀點分析評價試題是現代教學需要著重思考的問題.

[關鍵詞] 數學核心素養；數學評價；試題命制；能力立意；素養立意

引言

時代變化了，教育的要求變了，呼喚核心素養的出現. “核心素養是新課標的來源，也是確保課程改革萬變不離其宗的‘DNA，考試評價的方式和內容正在悄然地改變，圍繞發展學生的核心素養的教育評價體系正在逐步形成，未來三到五年的數學考試評價必將從“能力立意”轉變為“素養立意”.

正文

數學核心素養是具有數學基本特征的、適應個人終身發展和社會發展需要的人的關鍵能力與思維品質. 數學核心素養是數學課程目標的集中體現，是學生在數學學習的過程中逐步形成的.數學核心素養包括三個方面，六個關鍵詞：用數學的眼光觀察世界，發展數學抽象、直觀想象素養；用數學的思維分析世界，發展邏輯推理、數學運算素養；用數學的語言表達世界，發展數學建模、數據分析素養. 核心素養很重要，這一點估計沒人會反對. 但問題是，很多老師不知道如何去操作落實，這是擺在我們老師面前的現實問題. 林崇德教授給出這樣的指導意見：“核心素養具有可教、可學的外顯部分，同時也存在無聲、無形但可感、可知的內隱部分. 前者能夠在特定的情境下通過一定的方式表現出來，因此能夠有效地對其進行定量的測評……”基于此，筆者在試題的命制過程中進行了一些嘗試.

一、題目名稱

導數的幾何意義和函數不等式證明問題.

二、題目分析

1. 試題的命制思路分析

此題是基于數學情境命制的試題，試題素材來源于教材中導數的幾何意義，背景是函數f（x）=ex在x=0處和u（x）=lnx在x=1處的泰勒展開式.

第（Ⅰ）問直接考查導數的幾何意義.由于函數f（x）=ex和u（x）=lnx互為反函數，且f（x）在（0，1）處的切線m和u（x）在（1，0）處的切線n平行，把n和u（x）向左平移2個單位就得到m和g（x）=ln（x+2）. 因此引入參數a，構造新函數g（x）=ln（x+a）.控制參數a的取值范圍可保證f（x）>g（x），于是抽象出第（Ⅱ）問. 通過幾何畫板演示發現參數a有最大值，最大值是多少呢？（筆者注：我們猜想這個最大值與歐米伽常數有關）通過探索發現高中知識很難解決這個問題，于是給出相關數據，改為求參數a最大值的近似值.

2. 考查目標分析

本題在較復雜的數學情境下考查函數圖像在某一點處的切線與函數導數的關系，即導數的幾何意義，考查導數公式和導數運算法則、函數最小值、導數、函數零點的概念，考查考生靈活運用導數工具借助已知數據去分析問題、解決問題的能力，綜合考查考生的邏輯推理能力、運算求解能力、推理論證能力以及轉化與化歸、數形結合的思想.

3. 試題設問及解答過程中涉及的數學核心素養分析

（1）邏輯推理和數學運算素養

邏輯推理是指從一些事實和命題出發，依據邏輯規則推出一個命題的思維過程，主要包括兩類：一類是從特殊到一般的推理，推理形式主要有歸納、類比；一類是從一般到特殊的推理，推理形式主要有演繹.數學運算是指在明晰運算對象的基礎上，依據運算法則解決數學問題的過程，主要包括：理解運算對象，掌握運算法則，探究運算方向，選擇運算方法，設計運算程序，求得運算結果等.

第（Ⅰ）問的設計面向全體考生，要解決這個問題，考生要具備畢業水平的邏輯推理素養：在對曲線切線的概念充分理解的基礎上，由分析法知，需要求切點坐標和切線的斜率；還要具備畢業水平的數學運算素養：準確應用導數公式和求導法則進行導數運算就可以求切點坐標和切線的斜率，再寫出切線的點斜式方程.

（2）數學建模和直觀想象素養

數學建模是對現實問題進行數學抽象，用數學語言表達問題、用數學知識與方法構建模型解決問題的過程，主要包括：在實際情境中從數學的視角發現問題、提出問題，分析問題、構建模型，求解結論，驗證結果并改進模型，最終解決實際問題.筆者認為也應包括構造新的數學模型解決數學問題的過程. 直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解和解決數學問題的過程，主要包括：借助空間認識事物的位置關系、形態變化與運動規律；利用圖形描述、分析數學問題；建立形與數的聯系；構建數學問題的直觀模型，探索解決問題的思路.

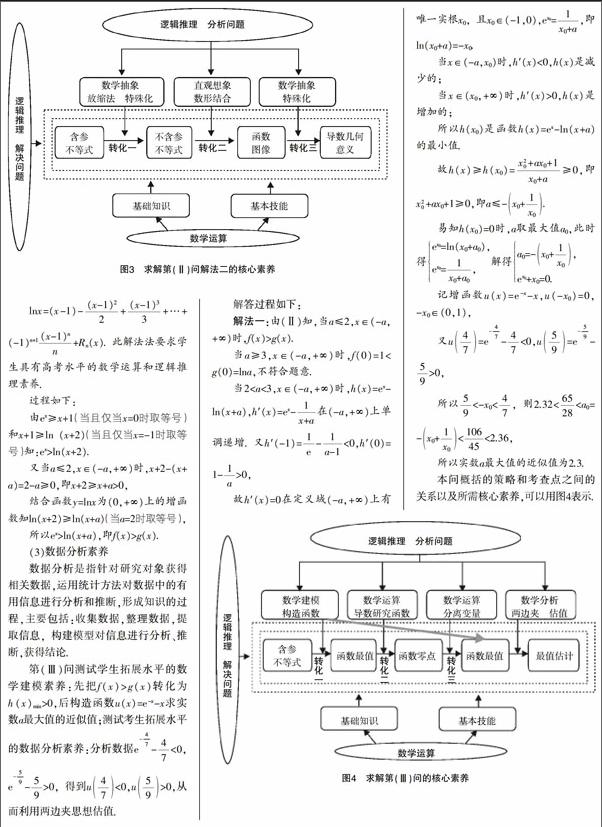
解答（Ⅱ）問時要把f（x）>g（x）轉化為h（x）min>0，能測試學生高考水平的數學建模素養和數學計算和邏輯推理素養：在求解過程在發現不易判斷h′（x）=ex-的正負號，得不到h（x）的單調性，但借助圖形可以發現當a≤2，x∈（-a，+∞）時ex-ln（x+a）≥ex-ln（x+2），借助放縮法把問題轉化為證明ex-ln（x+2）>0. 這就考查了學生的直觀想象、數學運算和邏輯推理的素養.

下同原題第（Ⅲ）問的解法.

從以上分析可以看出，在解答本題時起決定作用的是邏輯推理、數學建模、直觀想象、數學運算和數據分析五大核心素養. 在將新問題轉化為舊問題，復雜問題轉化為簡單問題的過程中，數學核心素養起著重要的作用，而知識和技能只有在具體求解時才能發揮作用.

數學核心素養雖劃分為三個方面，六個關鍵詞，但它們既有獨立性，又相互交融，形成一個有機整體. 用數學的眼光觀察世界，即人從外界輸入信息；用數學的思維分析世界，即人處理信息；用數學的語言表達世界，即人輸出信息.