數學概念教學探究
——以三角函數的概念為例
?青島大學數學與統計學院 鄭舒婷 李明蘭
1 問題提出
數學概念是學生學習數學的基礎,數學概念的理解程度對學生的數學思維產生直接的影響,因此,數學概念是數學知識教與學中的核心部分.美國數學家杜賓斯基(EdDubinsky)在皮亞杰提出的“反思性抽象”的基礎上提出了四個階段的數學概念學習[1].Vinner和Hershkowitz于1980年提出了概念表象和概念定義理論,概念表象和概念定義是同一概念的兩個方面,是概念形成的共同體.教育部于2020年頒布了《普通高中數學課程標準(2017年版2020年修訂)》(下文簡稱“《課標》”),根據《課標》的相關要求和規定,對人教A版教科書進行了全面的修訂,三角函數的內容變化較大,三角函數的概念更加凸顯函數的本質,學生對于三角函數概念的理解存在困難.因此本研究以三角函數的概念為例,把概念理解模型融合到APOS理論的四階段中來指導數學概念教學.
2 理論基礎
APOS理論是一種建構主義數學學習理論,數學概念的建構需要經歷四個階段,分別為操作(Action)、過程(Process)、對象(Object)、圖式(Schema)這四個階段,該理論的主要心理機制為內化與凝聚[1].APOS理論的四個階段在學生數學概念的學習中能很好地體現學生真實的思維活動,為學生真正理解數學概念,形成豐富且正確的概念表象提供了可能,最終期望達到對概念的靈活使用.Vinner和Hershkowitz于1980年提出了概念表象和概念定義理論,后由Tall和Vinner于1981年對該理論進行了發展,Morre于1994年對該理論進行了修定,他認為除了概念定義和概念表象外還存在概念理解的第三個方面,“概念使用”,也就是利用概念定義來解決數學任務,比如定義產生證明和定義構造例子等[1].概念定義是直接描述的,它是以詞語和符號的形式,被教師或教科書用來定義數學概念的[1].概念表象并非直接描述,它是個體頭腦中與概念有關的整個認知結構,包含思維圖像、相關性質和過程等[1].在數學概念的學習過程中,有的學生通過死記硬背有定義而無表象,有的學生通過直觀感受只有表象而無定義,學生無法深度理解數學概念,更無法靈活地使用數學概念.因此,教學中要將APOS理論與概念理解模式相融合,利用APOS理論指導概念教學的過程,在“操作”“過程”等階段中形成正確的概念表象并正確理解概念定義,在“對象”和“圖式”階段,幫助學生正確使用概念,形成概念網絡.
3 數學概念的教學過程設計
3.1 創設活動情境,滲透表象和定義
這里的“活動”是指個體通過一步一步的外顯性(或記憶性)指令去變換一個客觀的數學對象[2].教師通過創設活動情境,促使學生動手操作,直觀地感知概念,并且在其操作過程中滲透概念的本質.舉例來說,在三角函數概念的教學中,教師通過多媒體展示生活中的周期現象,如齒輪的旋轉、摩天輪的轉動、交變電流等.這些周而復始的現實問題無法用已經學過的指數函數、對數函數以及冪函數等來刻畫,那么該用什么樣的函數模型來研究這些周期性的變化呢?這樣設計的意圖在于讓學生明確接下來學習三角函數的必要性,初步感受現實生活中的周期現象,并在頭腦中形成三角函數這一概念的正確表象,即三角函數是刻畫勻速圓周運動或周期變化現象等的函數模型.
3.2 呈現探究過程,歸納概念特征
當多次重復某一操作,這種類似機械化的操作就會被內化為一種稱作“程序”的心理結構,頭腦中的這一“程序”便可以指揮學生的行動,而不需要外顯的指令進行具體的操作,有的學生甚至可以逆轉程序或與其他相關程序結合.
舉例來說,在三角函數的教學中,學生可以從函數的角度重新認識銳角三角函數,可以設置如下問題.
問題1你能從函數三要素的角度來解釋銳角三角函數嗎?
問題2你能用平面直角坐標系中點的坐標表示銳角三角函數嗎?
在問題2中教師可提示“單位圓”,同時引出用單位圓上點的坐標來定義任意角的三角函數,給出三角函數的定義.接下來,就需要來說明定義的合理性.
問題3你能從函數的角度來說明對于角終邊上任意一點P(x,y)和任意角α之間的關系嗎?
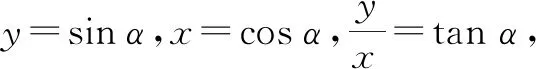
3.3 建構對象整體,把握概念本質
當個體能把這個“過程”作為一個整體進行操作和轉換的時候,這個過程就凝聚為一種心理“對象”,這時,個體可以操控對象去實施各種相關的數學運算[2].舉例來說,在三角函數概念的教學中,通過前兩個階段已經明確了三角函數的定義,現進行任意角三角函數概念的初步應用.
例1y=sinα和z=sinβ表示同一個函數嗎?
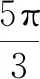
例3已知角θ的終邊過點P(-12,5),求角θ的三角函數值.
該階段的設計意圖在于通過例1,讓學生深刻認識到三角函數定義的形式和三角函數的本質之間的關系,讓學生明確三角函數概念的函數本質.例2、例3則是三角函數概念的簡單應用,并歸納出用定義求解三角函數值的步驟,加深對三角函數概念的整體認識.
3.4 建立綜合圖式,形成概念網絡
一個數學概念的“圖式”是由相應的活動、過程、對象以及相關的圖式所形成個體頭腦中的認知框架,其作用和特點就是決定某些刺激是否屬于這個圖式,從而就會作出不同的反應[1].舉例說明,在三角函數教學中,將任意角三角函數與銳角三角函數進行比較,探究二者之間的的聯系與區別.其次,還可以引導學生思考三角函數的“多元聯系表示”[3],即豐富學生的概念表象來幫助學生深入理解概念,正確使用概念.
經過活動、過程、對象這三個階段,此時三角函數的概念已經以一種綜合的圖式存儲在學生的頭腦中.這一綜合圖式不僅包括學生已有函數的相關知識、銳角三角函數的知識,還包括新建構的任意角的三角函數的概念、基本性質以及任意角三角函數與銳角三角函數的區別和聯系.
4 結束語
APOS理論不僅適用于大學教學,同樣適用于中學階段數學概念的教學.在APOS理論概念學習四階段的指導下,幫助學生形成正確的概念表象,并通過概念使用加深對概念的理解,把握概念的本質,將不同的概念不斷地納入到學生的概念系統中,形成自己的概念網絡.

