基于截面SEM 數據特征的微塵三維形貌建模方法

2023-03-28 04:32:48周林宏何光宇臧順來

航空學報 2023年4期

周林宏，何光宇，2，臧順來，*

1．西安交通大學機械工程學院，西安 710049

2．空軍工程大學等離子體動力學重點實驗室，西安 710038

軍用直升機或運輸機面臨在沙漠、戰場前線等惡劣環境中起降情形，這些大氣環境中常含有砂塵等微小顆粒物，其隨空氣被吸入發動機后，會對發動機壓氣機葉片產生砂塵沖蝕磨損，影響發動機的氣動性能，嚴重時甚至導致發動機葉片的斷裂失效，給發動機的可靠性和安全性等帶來惡劣影響［1-3］。火星車在火星表面工作時，不可避免地會受到火星塵的影響，其中最直接的影響是微塵附著在太陽能電池表面導致太陽能電池輸出功率下降。微塵環境對航空航天裝備的運行性能有著不利影響，為加強航空航天裝備的防塵設計需要對微塵展開研究。

微塵的幾何形貌是影響砂塵沖蝕失效的重要因素，為探究砂塵沖蝕失效機理，需要研究微塵的幾何形貌［4-6］；氣固兩相流對葉片氣動特性影響研究中需要通過風沙顆粒的外形等相關特性進行研究［7-9］；微塵軌跡分析需要通過微塵的形狀分布對其反彈特性進行研究［10］；同時微塵外形特征也是影響微塵吸附特性的重要因素。微塵的三維形貌是微塵特性的重要影響因素，因此研究微塵的形貌特征是加強航空航天裝備防塵設計的關鍵所在。目前常用的微小顆粒物幾何特征測量方法有測定顆粒粒徑的沉降法、篩分析法、激光衍射法、電阻法，以及觀察顆粒形貌的顯微鏡法［11-12］。每種測量方法都存在一定的適應范圍及缺點。例如，沉降法存在測量速度慢，重復性差的缺點；篩分析法對于微小顆粒難以測量；激光衍射方法的測量誤差與粒徑分布與形狀的不規則性存在正相關性；電阻法要求被測微小顆粒物具有良好的導電性；顯微鏡法代表性差無法獲取具有統計意義的數據［13］。但僅通過分析測量儀器并不滿足對于微塵顆粒形貌的研究需要，其他研究工作者也結合其他方法進行對顆粒三維形貌特征的探索，Komba 等［14］采用3D 掃描技術測量顆粒的形狀指標，基于顆粒的表面積、體積以及3 個正交方向的長度數據描述了顆粒的形狀特征。Alshibli 等［15］采用三維同步加速斷層掃描技術獲取了高分辨率的顆粒圖像，并且使用光學干涉技術計算了顆粒的表面紋理。Sun 等［16］采用三維掃描設備，引入了“橢球度”的概念來衡量顆粒的三維形狀。這些三維形貌的描述方法獲得了較大顆粒的球形度等整體的形狀參數，但是無法描繪更微小的顆粒以及顆粒的個體形貌特征。

傳統方法對顆粒外形特征的描述均存在一定的缺陷。目前已有一些研究人員引入圖像處理技術來研究微小顆粒物的三維形貌。 Jia 和Garboczi［17］總結了近年來，計算能力和三維圖像采集與分析技術的進步，使得顆粒形狀信息的測量、描述和應用取得的重大進展。Liang 等［18］引入了三維球度、圓度和粗糙度來定義粒子形態在一般形狀、局部角度和表面紋理這3 個尺度級別來對顆粒的三維形態進行評價。Zhou 等［19］提出了一種評價顆粒形貌的DIP 方法，通過分析采集到的砂粒投影圖計算砂粒軸徑比以及圓形度。基于二維圖像進行處理不能完整體現顆粒的三維形貌，因而其研究結果在多個個體的統計意義上才具有代表性，很難反映單一個體的幾何形貌特性［20］。上述分析顆粒是通過各個方向二維的截面或者投影圖像進行觀測分析，由于顆粒具有三維的形貌，僅僅依靠二維圖片只能分析某一特殊層的特征，不能完整地展現整個顆粒的形貌，而隨著計算機技術的發展，通過計算機輔助重構出顆粒的三維表面，更有利于分析顆粒的三維形貌特征。Peng 等［21］通過多視圖輪廓擬合和密集點云插值方法重建了磨損顆粒的三維表面。Zhou 等［22］在研究中采用計算機層析成像技術，重建了三維微塵的真實表面，提出了一種描述微塵三維球形度、圓度、和分形維數的方法，利用所提出的方法，對兩種天然砂粒的形貌特征進行了測量。張永弟等［23］提出了一種層間插值算法，提高了三維重構準確性。

現有微塵三維重構方法對毫米量級的微塵形貌特征研究較為有效，但不能夠滿足粒徑只有上述研究中1/10 甚至更小粒徑微塵的重構需求，原因在于對更小粒徑的微塵難以獲取其不同斷面之間的間距，因此微塵三維重構需要攻克難點和關鍵點是二維斷層圖像間距離的精確測定；而國軍標砂塵沖蝕磨蝕標準中對細沙顆粒物粒度分布要求為0～200 μm［24］，因此對于更小的砂塵顆粒三維形貌測量方法和技術仍需開展深入研究。選取粒徑100 μm 微塵作為研究對象，基于二維圖像，在保持微塵間相對位置固定的前提下，通過逐層剝離獲得高精度的微塵斷層二維掃描電鏡SEM圖像。對于三維形貌重構，通過在微塵間隙預置一定直徑鋼球，利用鋼球斷層截面的圓心坐標變化規律，斷層圖像對齊；利用鋼球斷層截面圓的半徑變化，實現斷層層厚精確測定；基于距離變換的層間插值方法，有效提高斷層間的分辨率，采用移動立方體算法重構了微塵的三維幾何模型。

本文提出的方法將完成微塵的三維形貌表征，形成微塵外形特性分析方法，對推進航空裝備的沖蝕防護、航空發動機氣體動力學研究具有重要作用，對航空航天裝備的防塵設計具有重要意義。

1 微塵斷層圖像試驗

1.1 微塵冷鑲試樣制備

選取的研究對象為粒徑100 μm 數量級（75～125 μm）的自制微塵。微塵試樣采用冷鑲的方法制備，制備微塵試樣時，埋入直徑1 mm 的精密鋼球。采用切割機將試樣切割為4 個部分，以消除試樣的冷縮變形。用3 000 目砂紙打磨試樣至露出鋼球截面。將微塵試樣放入噴金設備中噴金處理，噴金后試樣見圖1（a），每個視場內均埋入2 個精密鋼球。

采用冷鑲嵌的方法，微塵試樣會產生固化收縮現象，使試樣出現翹起、裂紋等問題。采用環氧樹脂鑲嵌出現的主要問題是固化后底面中心厚度會小于邊緣厚度，見圖1（b），厚度差約幾十微米。由于采用的微塵粒徑僅為75～125 μm，厚度差的存在會對圖像采集造成不利的影響，因此將鑲嵌后的微塵試樣沿直徑切割為4 個部分，得到4 個厚度差較小的試樣表面，減小固化收縮帶來的影響，見圖1（c）。

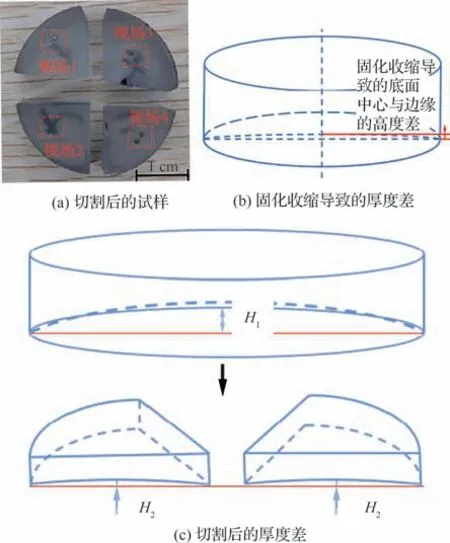
圖1 厚度差示意圖Fig. 1 Schematic diagram of thickness difference

制備試樣時，應將少量微塵顆粒與環氧樹脂和固化劑混合均勻，以保證試樣中微塵顆粒分布均勻，待固化與磨削工作完成后對制備的試樣進行篩選，部分試樣在光鏡下的成像如圖2 所示。圖2 中深色部分為鑲嵌基體，淺色部分為微塵截面，高亮部分為鋼球截面部分。為了方便圖像識別以及避免出現微塵堆疊從而影響三維重構的結果，應選取如圖2（a）和圖2（b）所示的圖像中微塵分布間隔較遠、堆疊可能性小的樣品作為微塵重構研究的樣品，應當避免選擇如圖2（c）和圖2（d）所示的微塵密集分布，極有可能產生微塵顆粒堆疊的樣品。

圖2 微塵試樣顯微圖像Fig. 2 Microscopic image of fine dust sample

1.2 斷層圖像

對微塵試樣采用3 000 目砂紙進行逐層剝離并采用SEM 試驗觀察微塵的二維形狀。視場1第1 層微塵截面的SEM 圖像如圖3（a）所示，圖中白色為精密鋼球，灰色為微塵截面，深色為樣品鑲嵌基體。微塵截面形狀復雜多樣，除幾何形狀接近凸多邊形，還有細長狀、斷裂狀、彎曲狀等。圖3（b）、圖3（c）和圖3（d）為該視場的第6、11、15 層微塵截面的SEM 圖像，隨著微塵試樣剝層的厚度增加，微塵截面形狀出現增大或者減小趨勢，也有一些微塵顆粒物消失。

圖3 微塵斷層圖像Fig. 3 Tomographic image of dust particle

2 圖像處理算法

2.1 微塵幾何特征

2.1.1 閾值處理方法

為獲取微塵二維截面輪廓，需要對圖像進行閾值處理、去除圖像雜質、提取邊緣輪廓。其中閾值處理具體過程如下所述。一幅數字圖像可視為一個函數f(x，y)，其中自變量是任意一像素點的坐標，函數值f為該點圖像的灰度。閾值處理即圖像的二值化［25］，閾值處理后f僅有2 個灰度值，0 或255。實現方法如下：首先給定一個合適的閾值Tcr，然后將整幅圖像中大于或等于Tcr的像素點灰度值賦為255，小于Tcr的像素點灰度值賦為0，從而得到僅有0 和255 這2 個灰度值的二值圖像函數g(x，y)，其數學表達式為

SEM 試驗得到的圖像中主要有3 種灰度等級，為了得到僅含有微塵截面和基體的二值圖像，需要先將白色的鋼球移除，然后再選擇合適閾值將圖像二值化。選擇閾值T1cr=200，使灰度值大于T1cr的像素點灰度值變為0，其余像素點灰度值不變，完成鋼球移除；選擇閾值T2cr=40，使灰度值大于T2cr的像素點灰度值變為255，其余像素點灰度值變為0，完成圖像二值化，視場1 第1 層微塵截面圖像處理結果見圖4。

圖4 圖像二值化Fig. 4 Binary image

2.1.2 移除小顆粒和邊界微塵

二值化后的圖像中通常含有雜質像素點，同時圖像邊緣的微塵截面并不完整，見圖4（b）。為準確識別微塵截面輪廓，需要將這些雜質像素點移除。實現過程為：①在當前圖像中標記連通區域，并計算每個連通區域的面積屬性；②尋找面積小于50 像素的連通區域，并把這些區域刪除，即把黑色區域中的白色雜質顆粒刪除；③使黑白像素翻轉，重復步驟①，刪除白色區域中的黑色雜質顆粒，視場1 第1 層微塵截面的處理結果見圖5（a）；④將圖像邊緣處的白色微塵截面刪除，見圖5（b）。

圖5 去除雜質Fig. 5 Remove impurities

提取獲得的微塵截面左上部分輪廓圖像如圖6 所示，微塵截面的輪廓邊緣不完全光滑，存在凹凸不平的現象。

圖6 微塵截面輪廓圖Fig. 6 Profile of dust particle section

2.1.3 像素與微塵尺寸的轉換

由于拍攝圖像時的分辨率可以不同，則相同實際尺寸下對應的圖像像素點個數也將存在不同。進行圖像處理的基本單位是像素，而構建微塵三維模型需要使用微塵的真實尺寸，因此需要對像素個數與實際尺寸進行轉換得到真實的尺寸。以圖像的左上角為原點構建二維坐標系，截取圖像當中的標尺部分，讀取寬度方向的第1 個黑色像素坐標與最后1 個黑色像素坐標，得到標尺兩端之間的像素數量，如圖7 所示。采用標尺的實際長度除以像素數量可以得到單個像素對應的實際尺寸：

圖7 圖像標尺Fig. 7 Image scale

式中：L為單個像素代表的實際長度；l為選取標尺的實際長度；X1為標尺起始點像素橫坐標；X2為標尺結束點像素橫坐標。

2.1.4 提取微塵幾何特征

對移除小顆粒后的二值圖像提取微塵幾何特征用于描述微塵的外形特性。如圖8 所示，微塵二維截面輪廓幾何特征指標的定義為最小二乘圓直徑是對砂塵截面輪廓偏差最小的圓直徑，其目標函數為

圖8 微塵形貌表征參數Fig. 8 Characterization parameters of dust particle morphology

式中：FLSC為最小二乘圓算法條件下的總距離誤差；x0、y0分別為最小二乘圓圓心橫坐標、縱坐標；xi、yi分別為砂塵輪廓上第i個點的橫坐標、縱坐標；R為最小二乘圓半徑。

最小二乘橢圓長短軸是對砂塵截面輪廓偏差最小的橢圓長短軸，其目標函數為

式中：FLSE為最小二乘橢圓算法條件下的總距離誤差；a為最小二乘橢圓短半軸；b為最小二乘橢圓長半軸；θ0為長半軸與x軸夾角；θi為砂塵輪廓上第i個點和最小二乘橢圓中心連線與長半軸的夾角。

最小外接圓直徑是可以包容砂塵截面輪廓的最小圓直徑，其目標函數為

式中：DMCC為最小外接圓直徑。

最大內接圓直徑是可以同砂塵截面輪廓內接的最大圓直徑，其目標函數為

式中：DMIC為最大內接圓直徑。

2.2 微塵三維重構

2.2.1 斷層圖像間距精確測定

二維斷層圖像間距離（層厚）的精確測定是基于二維圖像進行三維重構方法的難點和關鍵點。預置的1 mm 高精度鋼球在微塵試樣中，隨著微塵試樣剝層的厚度增加，鋼球截面輪廓圓半徑會發生改變，根據半徑變化規律可計算出相鄰斷層圖像間的距離。通過截面中的鋼球截面的半徑變化來獲取截面之間的厚度（見圖9），當兩截面位于同一半球，剝離層厚度為

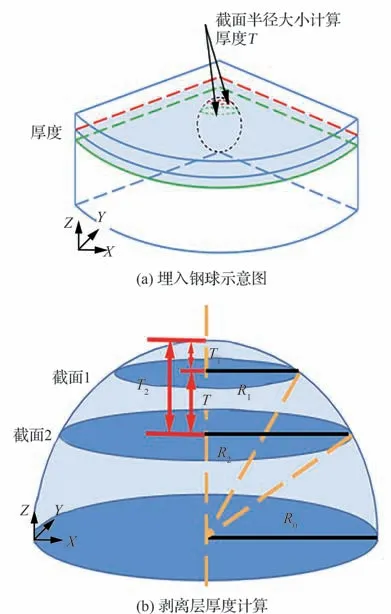
圖9 斷層圖像間距示意圖Fig. 9 Schematic diagram of tomographic image spacing

式中：R0為所用鋼球的半徑；R1為截面1 的圓半徑；R2為截面2 的圓半徑。

通過圖像處理對截面圖像進行識別得到鋼球截面的半徑大小，測定的截面半徑大小存在一定的誤差，因此計算的剝離層厚度也存在一定的誤差。假設圖像處理得到的截面圓半徑的誤差為ΔR，截面距頂端的距離為T1，T2=T+T1，基于此計算的厚度誤差為ΔT，則

因此，

對于同一尺寸的鋼球，即R0恒定，當兩截面之間的距離T一定時，厚度誤差ΔT與截面距頂端的距離T1有關，關系如圖10（a）所示。隨著截面尺寸越接近鋼球的最大截面尺寸，厚度誤差ΔT逐漸增大；當兩截面位于兩個半球時，誤差有所降低。

當兩截面之間的距離T和截面距頂端的距離T1一定時，厚度誤差ΔT與鋼球半徑R0有關，關系如圖10（b）所示。隨著鋼球半徑R0的增大，厚度誤差ΔT逐漸減小。

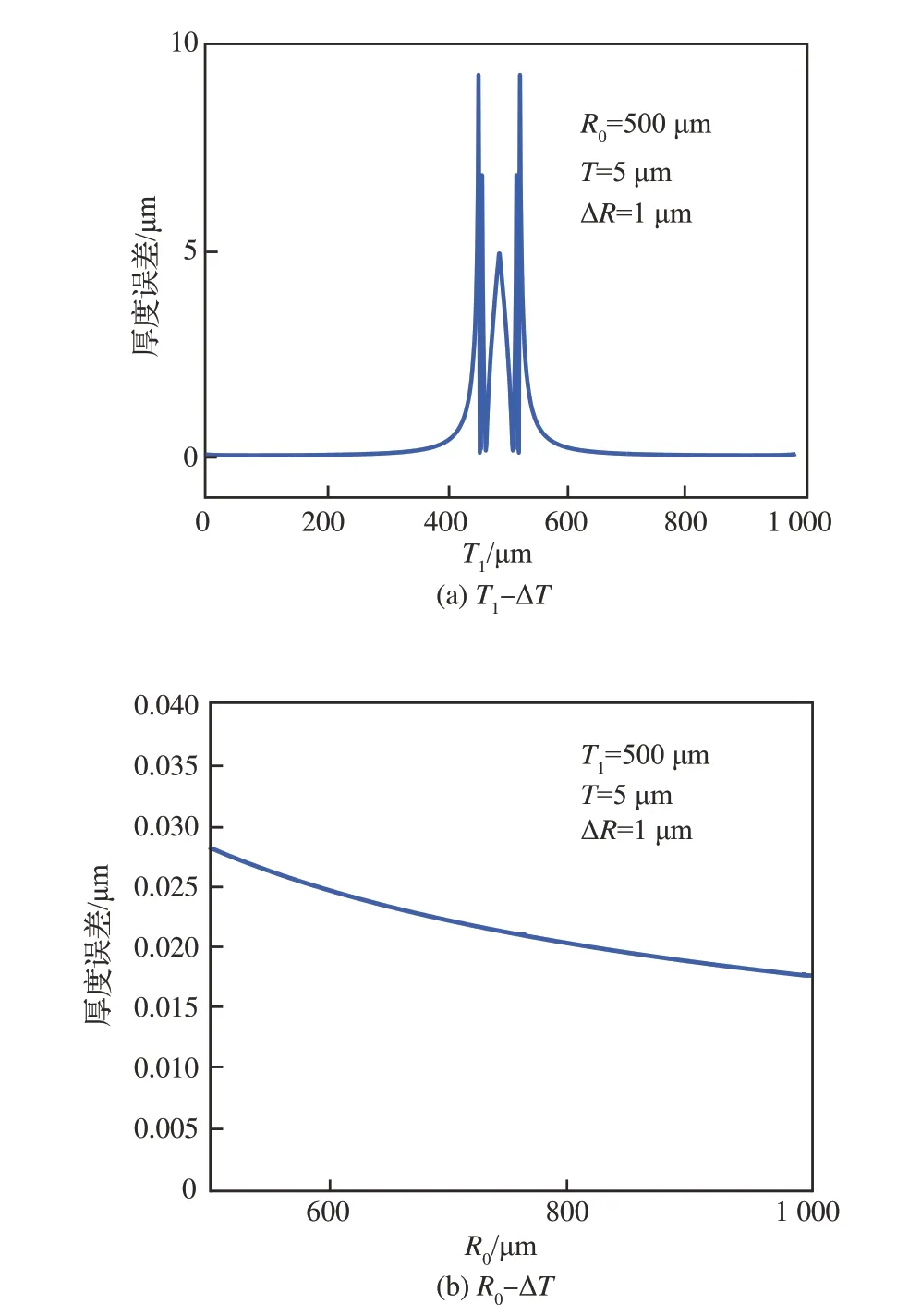
圖10 厚度誤差變化曲線Fig. 10 Thickness error change curve

2.2.2 斷層圖像間對齊

對于某一固定視場，拍攝過程會導致試樣不同斷層的截面圖像并不在同一位置，即微塵的各個截面圖像并未對齊，會導致重構得到模型發生偏移，無法還原目標的三維形貌，因此須調整截面圖像中微塵的位置，以保證各個微塵的不同截面圖像對齊。

基于圖像處理的方法識別出各個斷層圖像中的精密鋼球，并提取各個鋼球截面的圓心。采用獲取鋼球圓心坐標的方法對圖像提取鋼球截面輪廓，獲取構成鋼球輪廓像素點的坐標，采用輪廓像素點橫縱坐標的均值作為圓心坐標，根據輪廓區域面積獲取鋼球半徑值，方法的主要誤差來源于采集到的圖像的精度以及磨削過程中鋼球部分產生的毛刺。圖11 為磨削后鋼球截面部分的局部放大圖像，圖11（a）為帶有毛刺的圖像，圖11（b）為進行過光滑的圖像，對其進行圓心坐標和半徑的獲取得到的結果分別為（1 561.1，497.7）、（1 560.1，497.9）以及85.4、85.3，單位為像素，轉化為長度單位則圓心坐標產生的偏差為橫坐標方向1.796 μm、縱坐標方向0.359 μm，半徑產生的偏差為0.18 μm，約為半徑值的0.11%。因此磨削過程中鋼球的毛刺對鋼球截面圓心坐標以及半徑長度的獲取影響較小。

圖11 鋼球磨削產生的毛刺Fig. 11 Burr from grinding of steel ball

以圖像中心（1 024，768）為原點，設第k層截面中第i個鋼球的截面圓心坐標為Xik，下一截面的第i個鋼球的截面圓心坐標為Xik+1，每個截面的鋼球數量為2 個，可以求得第k層鋼球截面圓心間的正切值為

式中：X2k(2)、X1k(2)為圖像中第2 個和第1 個鋼球圓心的縱坐標；X2k(1)、X1k(1)為圖像中第2 個和第1 個鋼球圓心的橫坐標。

包含坐標旋轉變換參數θ的坐標變換矩陣為A(θ)。要保證前后圖像截面中的鋼球對齊，即要求的θ，滿足

包含坐標平移參數j、q坐標變換矩陣為B(j，q)，要保證前后圖像截面中的鋼球對齊，即要求的j、q，滿足

圖12 是選取視場1 的第2 層截面圖像對齊前后的對比圖。圖中，橫向與縱向平移變化以及旋轉角度分別為22.183 1、23.757 9、0.287°，旋轉中心為圖像中心。

圖12 圖像對齊Fig. 12 Image alignment

2.2.3 三維重構算法

三維重建算法主要可以分為面繪制與體繪制，其中面繪制在運算速度與運算量方面更有優勢，是三維重建中的主流方法。其中移動立方體（Marching Cubes， MC）算法［26］應用最為泛。MC 算法是一種用提取等值面（用三角面片近似表示）來表示物體表面的方法，見圖13。本文采用MC 算法進行微塵模型的三維重構。

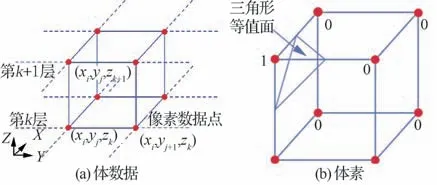
圖13 移動立方體算法示意圖Fig. 13 Schematic diagram of moving cube algorithm

通過SEM 試驗拍攝得到的二維斷層圖像分辨率為2 048×1 536，通過像素與實際長度的換算得到單個像素所代表的實際長度為1.796 μm，若斷層圖像之間的厚度大于1 μm 則進行插值至層間間距小于1 μm；單個微塵顆粒根據其體積大小，體素數量在40×40×200 至150×150×300 區間內；編寫圖像處理及三維重構程序，采用個人計算機進行重構，單個微塵顆粒重建時間為2.3 s。

為對該算法進行驗證，自主構建標準三維模型與隨機三維模型如圖14 所示，通過Materialise Magics 模擬逐層磨削過程，獲取斷層圖像進行三維重構，重構結果如圖15 所示。可以看到得到的重構結果與構建模型近似。

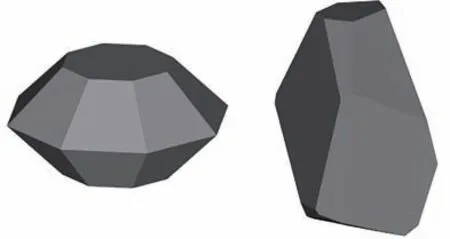
圖14 自主構建模型Fig. 14 Self-built models

圖15 驗證結果Fig. 15 Verification results

2.2.4 斷層圖像層間插值

在對斷層圖像進行三維重建的過程中，一般而言斷層間的距離大于斷層圖像像素間的距離。導致斷層圖像的層間的分辨率低于層內的分辨率，影響了三維重建的質量。采用層間插值的方法來提高層間的分辨率，即用圖像插值的方法在原來的斷層圖像間再生成中間斷層圖像。而層間插值處理中存在的主要問題是當斷層圖像間距大時，沒有任何方法可以插值出好的中間圖像即無法判斷兩個斷層圖像之間是否存在物體“消失”或“拓撲變化”現象，因此只有滿足斷層圖像間距較小時可以采用層間插值方法。

計算得到的斷層圖像間的間距為4～8 μm，而拍攝得到的圖像中，單個像素換算實際長度為1.796 μm。因此斷層圖像間的間距約為平面圖像中2～5 個像素的長度，滿足在斷層圖像間距足夠小的條件，因此可以忽略斷層圖像間的物體“消失”或“拓撲變化”現象，采用線性插值的方法進行近似插值獲取層間近似圖像。

關于插值模型，假設有2 幅二值圖像分別命名為gk和gk+1，并假設兩目標圖像為分別位于兩平行平面Z=Zk和Z=Zk+1上，對這兩目標圖像進行層間插值即得到在一系列平面Z=Zm(Zk＜Zm＜Zk+1)上生成的目標圖像gm，并使gm相似于gk和gk+1。

3 結果與討論

通過圖像處理得到了微塵截面輪廓圖，微塵截面輪廓的邊緣不完全光滑，存在凹凸不平的現象。通過圖像處理提取的微塵幾何特征參數如表1 所示，選用的微塵試樣的粒徑參數為75～125 μm，結果中微塵截面最小二乘圓直徑分布在0～130 μm 之間，約75%分布在55～100 μm 范圍內；試驗測定中微塵粒徑相對標準粒徑偏小，這是由于SEM 實驗所得到的是靠近微塵邊緣處的截面圖像，因此實驗得到的微塵粒徑相對于標準值偏小。試樣的最小二乘橢圓長軸分布在0～150 μm 范圍內，最小外接圓直徑分布在25～200 μm 范圍內，存在一部分微塵截面的最小外接圓直徑大于最小二乘橢圓長軸；最小二乘橢圓短軸分布在0～125 μm 范圍內，最大內接圓直徑分布在0～125 μm 范圍內，存在一部分微塵截面最大內接圓直徑小于最小二乘橢圓短軸，說明存在部分微塵呈現細長狀。

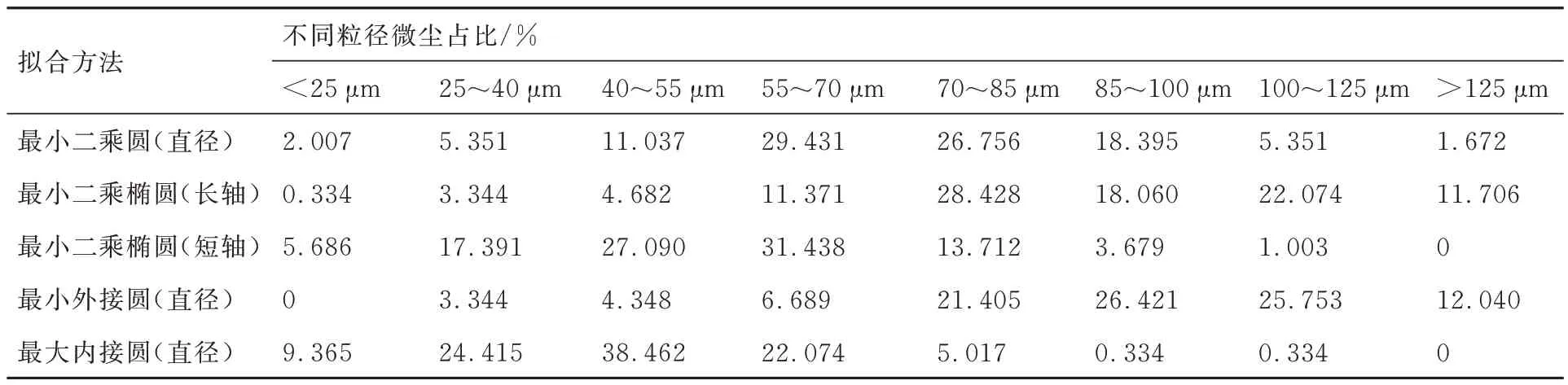
表1 微塵幾何特征Table 1 Geometric characteristics of dust particle

對于最小二乘圓直徑，試樣中55～100 μm 范圍的微塵最多，約占整體的75%；對于最小二乘橢圓長軸，試樣中70～125 μm 范圍的微塵最多，約占整體的70%；對于最小二乘橢圓短軸，試樣中40～85 μm 范圍的微塵最多，約占整體的70%；對于最小外接圓直徑，試樣中70～125 μm范圍的微塵最多，約占整體的75%；對于最大內接圓直徑，試樣中25～70 μm 范圍的微塵最多，約占整體的75%。每個試樣的5 個參數之間均存在一定的差異，因此微塵中僅存在少量接近圓形的微塵截面。

根據移動立方體算法重建得到了500 個微塵的三維模型，其中幾種典型的微塵三維模型如圖16 所示。其中常見的微塵形狀分為不規則多棱角狀（見圖16（a））、規則棱柱狀（見圖16（b））、尖角狀（見圖16（c））、規則多面體狀（見圖16（d））、棱錐狀（見圖16（e））、扁平片狀（見圖16（f））、長條狀（見圖16（g））、階梯狀（見圖16（h））、凸臺狀（見圖16（i））。而典型砂塵沖蝕仿真中所采用的微塵模型多為球狀、棱柱、棱錐等［4-6］，與真實微塵的形貌有著較大的差別，可以推測采用真實的微塵模型進行有限元數值模擬將有利于提高砂塵沖蝕計算的精度。