基于GA-SVR 的薄壁葉片輔助支撐布局優化方法

鄭志陽，張陽，張釗，吳寶海，*，張瑩

1．西北工業大學 航空發動機高性能制造工信部重點實驗室，西安 710072

2．西北工業大學 航空發動機先進制造技術教育部工程研究中心，西安 710072

葉片作為航空發動機的核心零部件，其加工質量與加工精度直接影響航空發動機的氣動性能和服役壽命。數控銑削作為一種高精度、高效率的加工方式，廣泛應用于航空發動機中壓氣機葉片的精密成形。然而，作為一種典型的復雜曲面薄壁件，在銑削加工過程中葉片很容易受切削力的影響發生“讓刀”，也即彈性變形。這使得銑削過程中刀具的實際切削位置相對理論切削位置出現偏離，導致葉片的加工精度不達標，從而影響發動機服役性能［1］。因此，研究如何抑制壓氣機葉片在加工過程中產生的彈性變形，對于保證其加工精度，提高發動機性能具有重要意義。

控制薄壁件加工彈性變形的前提是實現對變形的預測，這也一直是眾多學者的研究熱點。曹玉杰［2］基于加工變形柔性迭代算法建立了復雜曲面薄壁件的五軸銑削加工變形預測方法。黃澤華等［3-4］在考慮銑削力與彈性變形耦合效應的基礎上，忽略銑削過程中材料去除對葉片加工剛度的影響，建立了薄壁葉片點銑加工彈性變形的迭代計算格式。Li 等［5］基于CWE 模型計算切削力并將其離散到整個刀齒嚙合區域，然后采用有限元法建立了讓刀導致的薄壁葉片五軸側銑加工型面誤差預測方法，同時在仿真過程中采用了結構剛度修正法避免彈性變形導致的網格重繪。

薄壁件加工彈性變形的控制方法主要有加工刀軌補償［6-7］，切削參數優化［8］，裝夾布局優化［9-10］等方法。其中，合理的裝夾布局方案不僅可以保證工件的定位準確度，而且能夠增強工件的加工剛度及切削穩定性。為了綜合控制大型薄壁件自重導致的變形以及裝配公差，有學者通過有限元法計算不同裝夾布局下的工件變形，并基于花授粉算法［11］、社會輻射算法［12］等對裝夾布局進行優化。近年來，為了避免迭代優化過程中大量的有限元計算，提高裝夾布局優化效率，縮短夾具設計周期，代理模型成為新的研究趨勢。該方法首先通過構建裝夾參數與布局優劣評價指標的樣本集合，其中布局優劣評價指標一般是工件的最大變形、平均變形、整體應變能等，而評價指標的數據來源可以是有限元仿真，也可以是生產現場數據［13］、然后通過神經網絡［14-15］、支持向量機回歸［16］，Kriging 模型［17］等方法訓練樣本數據集，獲得裝夾參數與評價指標之間的代理模型；最后在布局優化過程中采用代理模型替代有限元法計算評價指標，實現裝夾布局的快速優化。

此外，在薄壁件的加工過程中施加輔助支撐，如鏡像銑、橡皮泥、磁流變材料［18］等也是可行的加工變形控制方式。基于鏡像銑的概念，彈簧阻尼器［19］與氣射流［20］也被用于薄壁件的切削加工輔助支撐，通過與刀具做鏡像運動為工件提供阻尼，進而降低加工振動與變形并提高工件表面質量，但鏡像類輔助支撐一般只能用于薄板類零件的加工。針對精鍛葉片榫根的精加工，Wu 等［21］以Peek-GF30 材料作為支撐頭設計了自適應四點輔助支撐夾具，有效降低了葉片榫根精銑過程中葉身支撐部位的應力集中與裝夾變形。Wang 等［22］設計了一種與機床協同控制的四點裝夾支撐平臺，在加工過程中對處于懸臂狀態的葉片榫根進行支撐并且能夠自動避讓刀具。針對薄壁框型件的銑削加工，Zeng 等［23］通過多點輔助支撐抑制薄壁件的加工振動，并對輔助支撐的布局和數目進行了同步優化。然而，針對薄壁葉片的葉身型面銑削加工輔助支撐，目前還缺少相應的研究。

針對薄壁葉片的加工彈性變形問題，設計了四自由度回轉輔助支撐機構增加葉片的加工剛度，并提出了一種基于GA-SVR 的薄壁葉片輔助支撐布局優化方法。第1 節建立了綜合考慮材料去除以及銑削力與彈性變形耦合效應的葉片銑削加工有限元仿真預測模型；第2 節基于拉丁超立方設計和有限元仿真模型生成樣本集，再以支持向量機回歸訓練樣本集，獲得評價指標的代理預測模型；第3 節采用精英策略遺傳算法對薄壁葉片的輔助支撐布局進行優化；第4 節進行薄壁葉片銑削加工及三坐標測量實驗，驗證本文方法的有效性；第5 節得出結論。

1 薄壁葉片輔助支撐銑削有限元仿真建模

葉片型面特征復雜，并且其加工剛度隨著銑削過程中的材料去除而不斷下降，同時加工彈性變形與切削力之間呈現出很強的非線性耦合關系，這導致很難通過解析的方法實現葉片加工彈性變形的準確預測。因此，在綜合考慮材料去除以及銑削力與彈性變形耦合效應的基礎上，采用有限元法預測薄壁葉片的加工彈性變形。

1.1 考慮材料去除的葉片銑削仿真建模

1.1.1 葉片模型前處理

以航空發動機的壓氣機葉片為研究對象，模型如圖1 所示，材料為TC4 鈦合金。

圖1 葉片幾何模型Fig. 1 Geometric model of blade

1） 葉片網格劃分

在精加工過程中，葉片毛坯余量所剩無幾，葉片的剛度隨著材料的逐步去除而不斷下降。為了模擬葉片切削過程中的材料去除，在Hypermesh 軟件中為葉身型面的余量層單獨劃分網格，整個葉片模型總計131 360 個單元。

2） 邊界條件的施加

大型葉片在銑削過程中通常采用榫根固定，葉尖處施加頂尖約束的裝夾形式。為了增強葉片弱剛性區域的加工剛度，為葉片額外增加桿狀物理輔助支撐。因此，在仿真過程中需要依次限制榫根節點所有的自由度，葉尖處的平動自由度以及輔助支撐處的法向自由度。

1.1.2 切削載荷的確定及施加

當銑削力的波形頻率遠離機床固有頻率時，工件的彈性變形主要源于平均銑削力引起的靜態變形［24］。而且在切削過程中節點切平面內的切削分力主要參與切削，法矢方向的切削分力主要導致彈性變形。如圖2 所示，進行準靜態切削仿真，通過在一系列離散的刀軌節點上按照切削順序依次施加法向切削載荷來模擬動態的切削過程，計算當前切削位置的彈性變形，圖中Fnor，s表示第s個離散刀軌節點的法向切削載荷。

圖2 離散的切削刀軌Fig. 2 Discrete machining tool path

1） 切削力方向

采用ANSYS 軟件進行仿真求解，但ANSYS軟件無法直接沿任意矢量施加載荷。為了方便求解過程中切削載荷的施加，以及后處理階段中節點法向彈性變形的獲取，如圖3 所示，在前處理階段通過APDL 命令流依次將所有葉身型面節點坐標系的z軸旋轉至各自法矢方向，利用旋轉矩陣變換可得節點坐標系的旋轉角分別為

圖3 節點坐標系旋轉Fig. 3 Rotation of node coordinate system

式中：ns=(is，js，ks)為第s個節點處的曲面法矢；θs為繞x軸的旋轉角；βs為繞y'軸的旋轉角。

節點的法矢（i， j， k）通過UG 二次開發獲取，為便于后續葉身變形規律的分析，同時提取了節點在葉身型面上的等參數化坐標（u， v）。其中，第一條離散切削刀軌的節點信息如表1 所示。

表1 節點信息Table 1 Node information

2） 切削力大小

葉片通常采用五軸點銑進行加工，在銑削過程中時變的刀軸傾角勢必引起刀具和工件之間切削條件的變化。因此，在傳統經驗公式模型的基礎上，針對薄壁葉片的點銑加工刀位特點，引入刀軸傾角這一影響因素，建立了五因素經驗公式，并通過正交試驗設計以及多元線性回歸［3］，標定了球頭刀的五軸切削力經驗公式為

式中：Fx、Fy、Fz分別為切削力在x、y、z方向上的切削分力；ap為切削深度；ae為切削寬度；vc為切削速度；fz為每齒進給；φ為刀軸傾角。

如圖3 所示，通過獲取的節點法矢信息可以確定每個切削位置的刀軸傾角，將切削參數與刀軸傾角代入式（2）可計算得到每個節點位置的理論切削力。進一步地，將每個節點的理論切削力沿節點處曲面法矢方向投影，可獲得當前位置的法向切削力，并以此作為有限元仿真的切削載荷。法向切削力的計算公式為

式 中：Fx，s、Fy，s、Fz，s分別為第s個節點在x、 y、 z方向的切削分力。

1.1.3 材料去除效應仿真

通過ANSYS 軟件提供的單元生死法將余量層網格單元按照切削順序依次殺死來模擬切削過程中的材料去除，單元生死法無需將待“殺死”的單元從模型中直接刪除，而是對該單元的質量和剛度矩陣進行縮減：

式中：K0為待去除材料的初始單元剛度矩陣；Kd為材料去除后的單元剛度矩陣；ω=10-6為剛度縮減因子。

1.2 銑削力與彈性變形的耦合迭代格式

薄壁葉片在切削力的作用下發生的彈性變形使得實際切削深度小于名義切削深度，如圖4 所示，這導致實際的切削力小于按照名義切削深度計算得到的初始理論切削力。這也意味著銑削力與彈性變形之間是互相耦合的關系。傳統的薄壁件銑削加工彈性變形預測方法直接使用名義切削深度計算理論銑削力，并且僅通過一次有限元仿真計算葉片的加工彈性變形，完全忽略切削力與彈性變形之間的耦合效應，導致預測精度不高。

圖4 銑削力與彈性變形的耦合效應Fig. 4 Coupling effect between milling force and deflection error

為了更準確的預測葉片的加工彈性變形，建立銑削力與彈性變形的耦合迭代格式，如式（5）所示，以每次仿真計算得到的加工彈性變形修正理論切削深度，重新進行切削力的計算，這樣多次反復耦合迭代直至收斂，獲得最終的加工彈性變形預測值。

式 中：h=1，2，…，n；a0p，s和ahp，s分別為第s個節點的理論切削深度和經過h次迭代后的切削深度；δhs為第s個節點在h-1 次迭代后經有限元計算得到的法向彈性變形；Fh-1s為第s個節點在h-1 次迭代時的切削力：

此外，彈性變形導致的材料去除不充分使得預先劃分好的余量單元在真實切削過程中只有部分體積被去除。因此，為了避免繁瑣的網格重繪工作，提高計算效率，如圖5 所示，通過“不完全”殺死待去除單元來模擬材料的不充分去除。如式（7）所示，這種單元的“不完全”殺死是通過在仿真過程中修正當前被切除網格單元的剛度矩陣實現的，修正系數為迭代過程中該單元上次計算所得變形值與其初始厚度的比值。

圖5 考慮變形的材料去除效應修正Fig. 5 Modification of material removal effect considering deflection error

式中：Kt0和Kth分別為第t個單元的初始剛度矩陣和經過h次迭代后的剛度矩陣；ωht為第t個單元在第h次迭代時的剛度修正因子；δth為h次迭代后第t個單元的彈性變形值，此處取該單元最近節點的變形值；a0p，t為第t個單元的理論切削深度。

以葉盆型面上某一個節點為例，對其加工彈性變形進行耦合迭代運算，直至前后兩次迭代所得變形的變化率小于設置的收斂精度，該節點在迭代7 次以后收斂，迭代過程如圖6 所示。

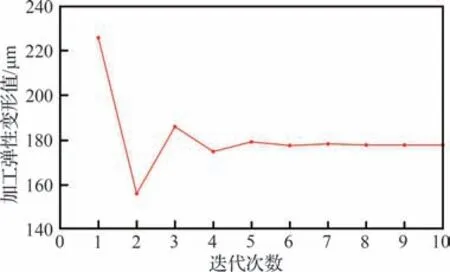
圖6 節點變形迭代過程Fig. 6 Iterative process of node deformation

1.3 葉片加工彈性變形迭代預測算法

綜合考慮葉片精銑過程中的材料去除及銑削力與彈性變形之間的耦合效應，聯合ANSYS與MATLAB 軟件設計了薄壁葉片銑削加工彈性變形迭代預測算法如圖7 所示，其步驟如下：

圖7 葉片加工彈性變形預測流程圖Fig. 7 Prediction flow chart of blade deflection error

步驟1依據銑削力經驗式（2），按照切削順序求解出每個節點的初始法向切削力，然后在ANSYS 軟件的APDL 腳本程序中增加相應布局下的輔助支撐位置約束。

步驟2APDL 程序讀取上次迭代求解得到的節點法向切削力，再由MATLAB 調用ANSYS 后臺執行該APDL 腳本程序，求解所有離散刀軌節點的彈性變形值并且輸出。

步驟3將獲得的所有節點彈性變形值代入式（5），更新各個節點處的切削深度，再通過式（6）更新計算每個節點的法向切削力。

步驟4按照式（7）根據當前節點變形值計算剛度修正因子，然后通過APDL 程序修正葉身待去除單元的剛度矩陣。

步驟5開始銑削力與彈性變形的耦合迭代循環運算，將更新的法向切削力導入APDL 程序中，計算下一代每個節點的彈性變形量。

步驟6對比各個節點前后兩次彈性變形量的變化率是否小于設定的精度e，若收斂則輸出當前所有節點的彈性變形量，得到葉片整體的彈性變形分布。

1.4 葉片加工彈性變形規律

定義葉身前緣到后緣為u方向，也即弦向，葉尖到葉根為v方向，也即展向。以等參數坐標為基準，繪制由加工彈性變形迭代預測算法得到的葉身型面加工彈性變形分布，如圖8 所示。

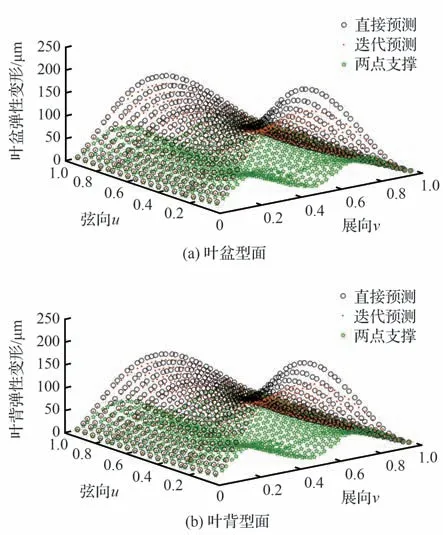
圖8 葉身型面加工彈性變形分布Fig. 8 Distribution of blade profile machine deflection error

分析葉身型面的加工彈性變形規律：

1） 葉身銑削加工彈性變形整體呈現馬鞍形，沿u向先減小后增大，沿v向先增大后減小，其原因在于：葉身弦向中部區域僅發生彎曲變形，而前后緣在切削力的作用下同時發生彎曲和扭轉變形；葉身展向中部則是由于無約束剛性差，使得其加工彈性變形大于葉尖和葉根。

2） 直接預測法得到的加工彈性變形明顯大于迭代預測所得，其原因在于：直接預測法忽略了切削力與彈性變形之間的耦合效應，其計算結果僅相當于迭代預測法的初代計算值。

3） 在葉身中部v=0.5 截面處施加兩點輔助支撐后，葉盆與葉背曲面的加工彈性變形得到顯著抑制，而且均勻程度也得到明顯提升，這表明為葉片增加加工輔助支撐是有效的。

2 基于SVR 的加工彈性變形代理預測模型

盡管第1 節建立的有限元模型能夠較好的預測薄壁葉片的整體加工彈性變形，但單純的有限元法不利于后續輔助支撐布局優化過程中大量的加工彈性變形計算。而基于SVR 的代理預測模型則有效解決了優化過程中目標變形特征的快速計算問題。

2.1 基于OLHD 的輔助支撐布局設計

葉片的加工彈性變形量隨不同的輔助支撐布局而改變，而輔助支撐的數目和位置是布局方案的兩個關鍵參數。為了保證通過抽樣生成的支撐位置能夠定位在葉身型面上，通過等參數化坐標確定輔助支撐在葉身曲面上的位置。因此，輔助支撐布局優化的設計變量可表示為

式中：xi為第i種輔助支撐布局方案；m為支撐點數目；xij=(uij，vij)為第i種布局方案的第j個支撐點的等參數化坐標，其中，uij、vij∈[0，1]。

現有的研究成果表明，同一葉片截面上施加的輔助支撐超過兩點，對于加工彈性變形的抑制效果提升非常微弱，而多截面支撐則會顯著降低加工效率［25］。因此，為了提高加工效率并且避免多點桿狀輔助支撐對加工過程產生過多干涉，僅對加工過程中的薄壁葉片設置單截面兩點輔助支撐，布局設計變量可寫為

式中：由于兩個支撐點位于同一葉片截面上，則有vi=vi1=vi2。

為增加樣本點在設計空間分布的均勻性，基于最優拉丁超立方設計（Optimal Latin Hypercube Design， OLHD），針對葉盆型面生成不同的輔助支撐布局方案作為初始樣本輸入。采用有限元仿真計算相應布局方案下葉片的目標變形特征，也即最大加工彈性變形與整體變形均方差作為樣本輸出。最終，獲得100 組樣本數據如表2 所示。

為了提高后續葉片加工彈性變形預測模型訓練的識別精度，表2 中的樣本輸出數據在訓練前需要進行歸一化處理：

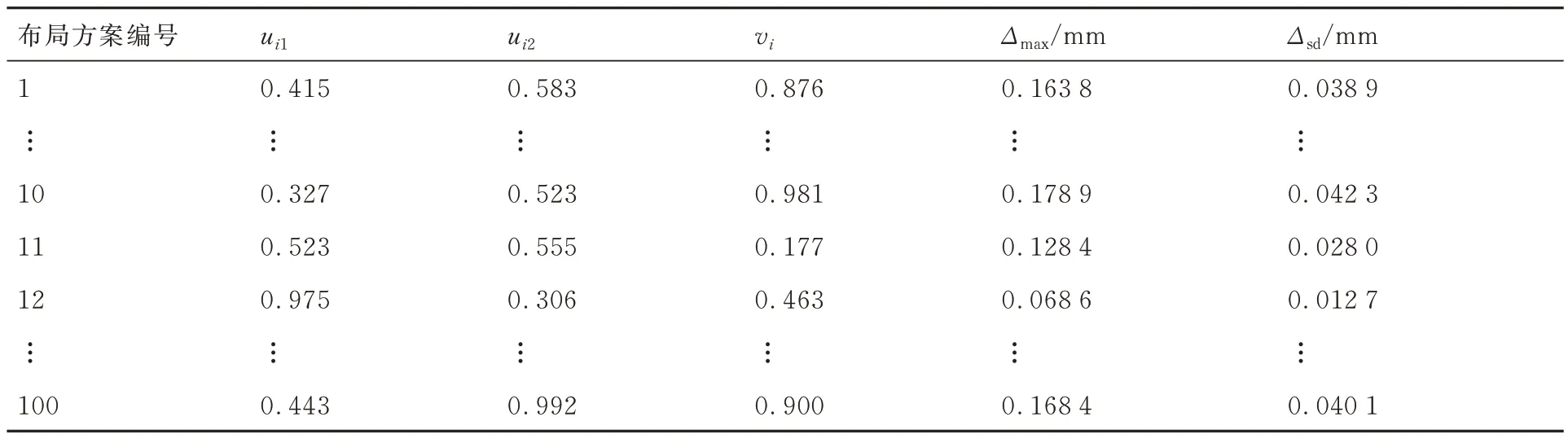
表2 葉盆布局方案采樣數據集Table 2 Layout scheme sampling data set of blade concave

式中：Δmax和Δmin分別為樣本輸出數據中的最大值和最小值；Δi為輔助支撐布局xi下葉身型面的最大加工彈性變形Δmax(xi)或整體變形均方差Δsd(xi)，yi表示歸一化后輔助支撐布局xi下的樣本響應值。

2.2 基于SVR 的代理模型構建方法

支持向量機回歸（Support Vector machine Regression， SVR）是 統 計 學 家Vapnik 提 出 的一種新的通用機器學習方法，在解決小樣本、非線性問題方面優勢顯著，并且具有較好的泛化性能［16］。其核心思想是將設計變量映射到高維空間，從而將低維非線性的問題轉化為高維空間中的線性回歸問題，其建模及求解過程［26］為

1） 給定訓練樣本集合

式中：xi和yi分別為第i種支撐布局及其變形響應，也即樣本輸入和輸出；n為訓練樣本數目。

2） 構建回歸模型

式中：f(X)為支持向量的回歸估計函數；φ(X)為將樣本映射到高維特征空間的非線性函數；w和b為待定參數，也是SVR 模型訓練的關鍵。

3） 模型參數求解

如圖9 所示，以f(X)為中心，構建一個寬度為2ε的間隔帶，并引入ε不敏感損失函數lε：當訓練樣本點落入此間隔帶時，也即回歸函數的返回值f(xi)與樣本輸出值yi的差小于等于ε時，則認為損失為0，也即訓練樣本可以被正確預測，而落在間隔帶之外的樣本點也就稱之為支持向量。于是SVR 問題可形式化為

圖9 SVR 基本原理Fig. 9 Rationale of SVR

引入松弛變量ξi和可將式（14）改寫為

式中：L為目標函數；C為正則化常數，也稱之為懲罰系數，C越大表示對誤差超過ε的樣本懲罰越大；ε則規定了SVR 函數的誤差限制。

根據結構風險最小化準則求解式（15）可得w和b，為了便于求解，引入拉格朗日函數并將L轉化為對偶形式：

式中：K(xi，xj)=φ(xi)Tφ(xj)為核函數；αi、ai為拉格朗日乘子。

求解式（16）可得最優解為

因此，可進一步得出參數w和b為

式中：nsv為支持向量的個數。

于是，將式（18）代入式（12）可得支持向量機的回歸函數為

4） 核函數的選取

SVR 通過核函數實現低維空間的非線性數據到高維空間的映射，解決了原始樣本空間中線性擬合困難的問題，并且不會增加數據數量。由于高斯徑向基核函數（Gaussian Radial Basis kernel Function， RBF）超參數少、精度高，具有很好的逼近特性，因此，選取RBF 構建SVR 的核函數：

式中：γ=1 2σ2，也即RBF 的幅寬；γ越大則高斯分布又瘦又長，容易過擬合；γ越小則高斯分布又矮又胖，平滑效應太大，無法在訓練集上得到較高的準確率，容易欠擬合。

2.3 基于GS-CV 的SVR 超參數優化

（C，γ）是SVR 模型訓練過程中的兩個關鍵超參數，其選擇沒有一定的先驗知識，本文數據集規模較小，為了充分利用有限數據獲得更高的預測精度，結合網格搜索（Grid-Search）和交叉驗證（Cross-Validation）進行了SVR 模型的超參數尋優，確定了最佳的超參數組合，具體優化步驟如下：

步驟1確定超參數（C，γ）的取值范圍。常用的取值范圍為[2-10，210]。

步驟2超參數網格化處理。由于參數范圍跨度較大，對超參數取值范圍以2 為底取對數可得(log2C，log2λ)∈[-10，10]，以0.25 為間隔進行交叉取值，總計可得種81×81=6 561種超參數組合。

步驟3K折交叉驗證。從100 組樣本數據中取80 份作為訓練數據集，20 份作為測試數據集。令K=5，再將訓練數據集均分為5 份，每份數據輪流作為驗證集，評價通過剩余4 份數據訓練得到的模型優劣，最后以均方預測誤差最小的超參數作為交叉驗證中的最優超參數。

步驟4超參數組合網格搜索。選取下一組超參數組合重復步驟3，直至找到均方誤差最小的超參數組合，作為當前樣本集合下的最優SVR 模型超參數。當模型訓練過程中出現不同的參數組合（C，γ）對應相同的交叉驗證精度時，一般選擇C更小的一組參數，以便于提高模型的泛化能力。

經GS-CV 優化后，分別獲得了葉盆最大加工彈性變形與整體變形均方差訓練模型的最佳超參數如表3 所示。

表3 最佳超參數組合Table 3 Optimal hyperparameter combination

2.4 SVR 代理預測模型精度評估

以葉盆為例，對其最大加工彈性變形和整體變形均方差兩個特征進行預測性能的評估，二者在訓練集和測試集的預測精度評價如表4 所示，其中均方誤差MSE 均接近于0，判定系數R2均接近于1。另外，從 圖10 中可以發現最大變形預測模型在測試集上的預測值和樣本值極為接近，這表明本文訓練的薄壁葉片加工彈性變形代理預測模型的預測性能非常優越。

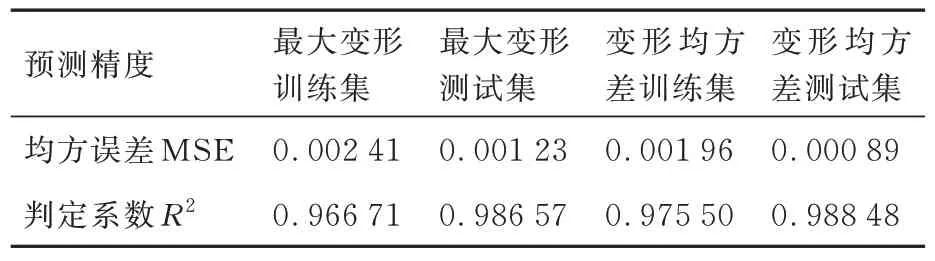
表4 模型精度評價Table 4 Evaluation of model accuracy

圖10 測試集的模型預測結果Fig. 10 Model prediction results on test set

3 基于E-GA 的輔助支撐布局優化方法

通過兩點桿狀輔助支撐來控制葉片在加工過程中由于彈性變形導致的加工誤差，合理的輔助支撐布局能夠最大程度地減小葉片的加工彈性變形。然而，生產現場大多憑借經驗確定輔助支撐位置，很難獲得最優的布局方案。因此，葉片輔助支撐的布局優化對于減小加工彈性變形、提高葉片加工精度具有重要意義。

3.1 輔助支撐布局優化建模

為了控制葉片的最大加工誤差，同時提高葉身加工誤差的均勻度，以薄壁葉片的最大加工彈性變形與整體變形均方差兩個特征最小為優化目標，建立兩點輔助支撐布局優化模型：

式中：Δj(xi)為葉身型面上第j個節點的變形值；為葉身型面上所有節點變形的平均值；分別為支撐桿與型面的切向與法向接觸力；X為裝夾設計可行域；μ為摩擦系數。

最大彈性變形與整體變形均方差2 個目標變形特征采用SVR 代理模型取代有限元法進行優化時目標函數的計算：

式中：fmax(xi)和fsd(xi)分別為通過SVR 代理模型預測的葉片在輔助支撐布局xi下的最大加工彈性變形和整體彈性變形均方差。

由于最小化葉身的最大彈性變形相應地會降低葉身整體變形的均方差，提高葉身變形的均勻程度。因此，為了降低優化目標的冗余，對葉身最大加工彈性變形和整體變形均方差的采樣數據進行皮爾遜相關性分析，通過式（23）可得二者的相關系數R=0.989 5，接近于1，這表明兩個特征高度正相關。因此，針對薄壁葉片輔助支撐的多目標布局優化問題，便可以簡化為針對最大加工彈性變形的單目標布局優化。

3.2 基于E-GA 的輔助支撐布局優化

精英策略遺傳算法（E-GA）將精英策略選擇算子引入傳統的遺傳算法中，通過將父代中的精英保留并替代子代種群中的適應度最低的個體，有效保證了在進化過程中出現的最優個體不會被選擇、交叉和變異操作所丟失和破壞，顯著提升了標準遺傳算法的全局收斂能力。鑒于此，采用E-GA 對葉盆的兩點輔助支撐布局進行優化，設置種群大小為40，進化代數為100，交叉概率為0.9，變異概率為0.1，精英選擇算子為0.025，優化流程及優化跟蹤圖分別如圖11 和12 所示。

圖11 輔助支撐布局優化流程圖Fig. 11 Optimization flow chart of auxiliary support layout

如圖13 所示，優化得到的葉盆最佳加工輔助支撐布局為xoptimal=[(0.32，0.42)，(0.90，0.42)]，對應的整體變形分布如圖14 所示，相比于無輔助支撐狀態，其最大加工彈性變形由178.2 μm 降到64.4 μm，下降63.9%；整體變形均方差由42.4 μm 降到12.9 μm，下降69.6%，對加工彈性變形的抑制效果顯著。同時，對比隨機兩點輔助支撐布局xrandom=[(0.26，0.59)，(0.84，0.59)]，可以發現最佳輔助支撐布局下葉盆型面的最大加工彈性變形更小，而且整體變形趨勢更加均勻。

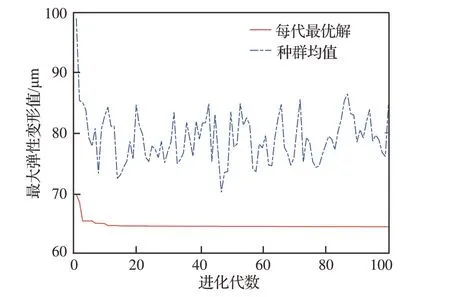
圖12 葉盆輔助支撐布局優化跟蹤圖Fig. 12 Tracking diagram of auxiliary support layout optimization for blade concave

圖13 葉盆最佳兩點輔助支撐布局Fig. 13 Optimal 2-points auxiliary support layout of blade concave

圖14 不同輔助支撐布局下的葉盆變形分布Fig. 14 Deflection error distribution of blade concave with different auxiliary support layouts

4 實驗驗證

為驗證建立的有限元仿真模型對薄壁葉片銑削加工彈性變形預測的準確性，以及輔助支撐對于葉片加工彈性變形的抑制效果，針對葉背和葉盆分別進行了精加工銑削及測量驗證實驗，加工參數如表5 所示，切削刀軌由商業軟件NX 11生成。此外，盡管彈性變形在加工后便會恢復，很難直接測量，但卻是薄壁件加工誤差的主要來源，因此，本文通過測量葉片加工誤差來表示加工彈性變形。

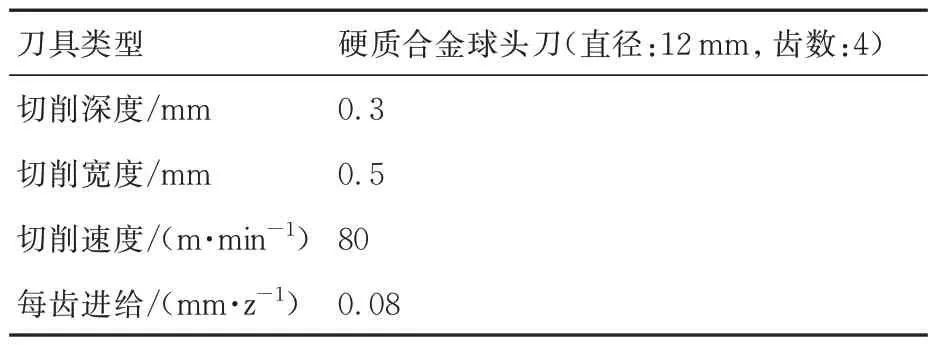
表5 加工參數設定Table 5 Machining parameter setting

4.1 加工彈性變形有限元仿真預測模型驗證

在葉背型面的精加工銑削完成后，如圖15 所示，通過三坐標測量機測量了葉背型面上2 條弦向曲線v=0.10， 0.50，以及1 條展向曲線u=0.90的輪廓，然后求解輪廓測點與理論曲線之間的法向間距，并以此作為每個測點位置的加工彈性變形。分別繪制3 條曲線的加工彈性變形的預測值與實際測量值，如圖16（b）～圖16（d）所示，可以直觀地發現采用有限元仿真模型預測的葉背型面加工彈性變形趨勢與實測的加工彈性變形趨勢比較吻合，每條曲線的預測誤差如表6 所示，其中最大平均預測誤差17.6%，最小平均預測誤差僅為6.6%，表明建立的薄壁葉片銑削加工彈性變形有限元仿真預測模型具有較高的準確性。

圖15 葉背銑削加工及測量實驗Fig. 15 Milling and measuring experiment of blade convex

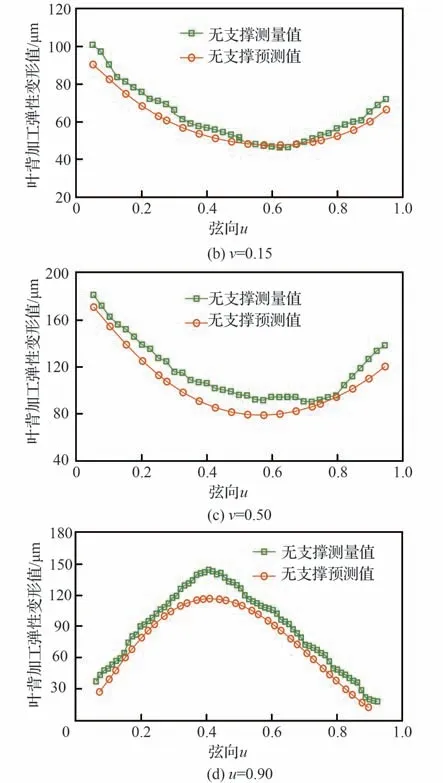
圖16 葉背加工彈性變形預測Fig. 16 Deflection error prediction of blade convex

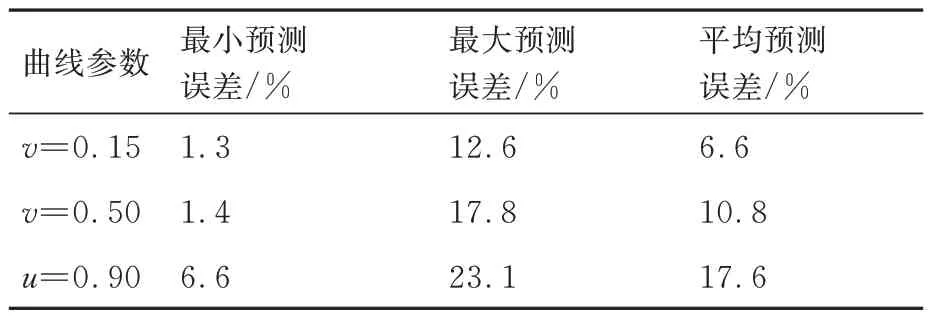
表6 葉背加工彈性變形預測誤差Table 6 Prediction error of blade convex deflection

4.2 輔助支撐加工彈性變形控制效果驗證

為實現薄壁葉片的輔助支撐銑削加工，設計了一種四自由度回轉輔助支撐機構，如圖17 所示。該機構通過定位塊在機床工作臺上實現x方向上的定位；在銑削加工過程中，葉身型面通過上下成對的球頭螺桿進行支撐，并且支撐高度在z方向可以調整，從而適應葉身上不同的曲面高度；固定框上設計有多個螺紋孔，實現了支撐螺桿在y方向上的定位。此外，回轉機構的設計使得該輔助支撐機構能夠繞x方向旋轉，可適應彎扭葉片不同的展向位置。

圖17 回轉式輔助支撐機構Fig. 17 Rotary auxiliary support mechanism

如圖18 所示，采用該輔助支撐機構進行了葉盆型面的精加工銑削，支撐布局采用第3 節優化得到的最佳兩點輔助支撐布局方案。

圖18 葉盆銑削加工及測量Fig. 18 Milling and measuring experiment of blade concave

同樣地，在加工結束后采用三坐標測量機測量了葉尖區域五條弦向曲線，分別是v=0.05 至v=0.25。如圖19 所示，分別繪制出無輔助支撐狀態下葉盆加工彈性變形的預測值、最佳輔助支撐狀態下的預測值以及測量值對比圖，可以看出：

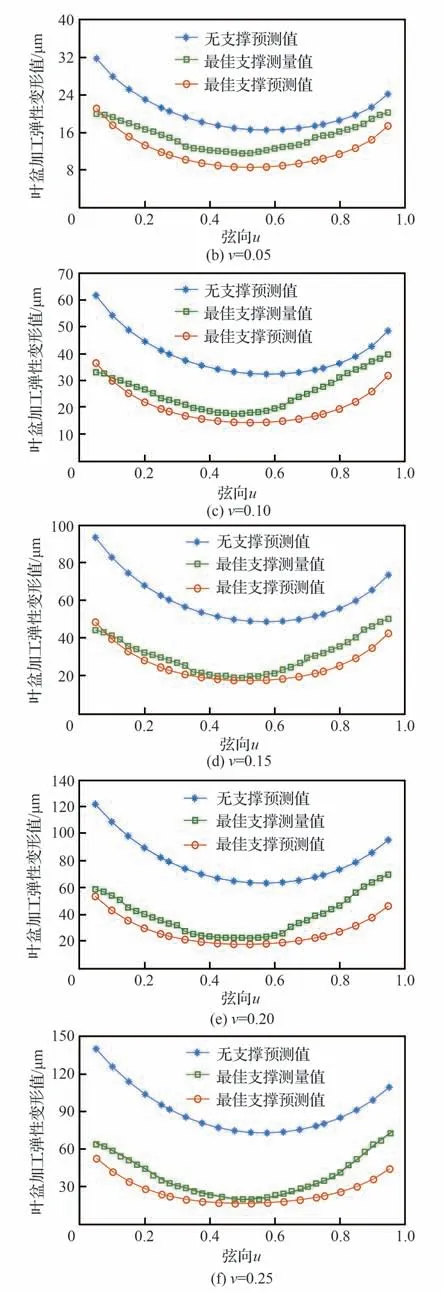
圖19 葉盆加工彈性變形預測Fig. 19 Deflection error prediction of blade concave

1） 在最佳輔助支撐下，薄壁葉片加工彈性變形的預測趨勢與測量趨勢基本一致。

2） 在增加輔助后，薄壁葉片的加工彈性變形得到了顯著的抑制，而且變形趨勢更加均勻。

為探究輔助支撐對于薄壁葉片加工彈性變形的抑制程度，定義節點的加工彈性變形抑制效果指標為

式中：zs和z's分別為節點s處的加工彈性變形預測值和實測值；ηs為節點s的加工彈性變形抑制效果指 標；num 為預測點數 目為預測節點的變形抑制效果平均值，也即平均抑制效果。

計算5 條參數化曲線整體加工彈性變形的最大、最小、平均預測誤差，以及平均抑制效果指標如表7 所示，可以看出：

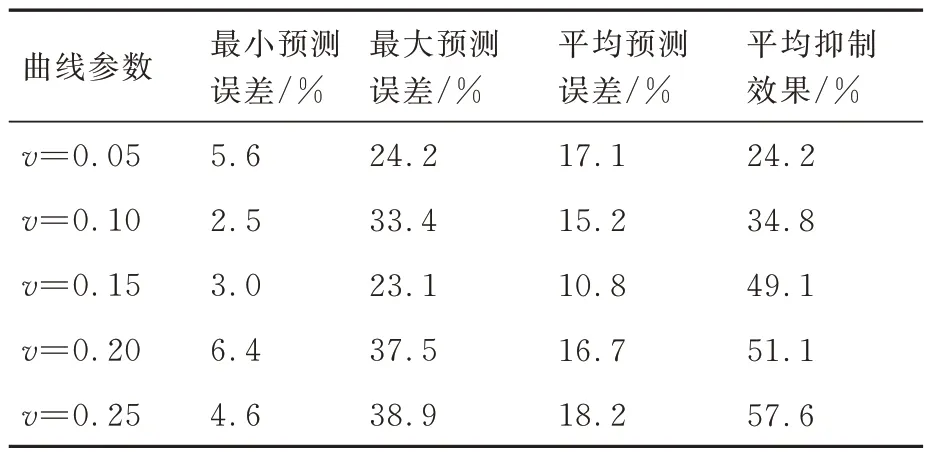
表7 葉盆加工彈性變形預測誤差Table 7 Prediction error of blade concave deflection

1） 輔助支撐下薄壁葉片加工彈性變形的平均預測誤差均在20%以下。

2） 隨著v值的增長，也即切削區域越靠近輔助支撐區域，輔助支撐對于加工彈性變形的平均抑制效果愈發顯著，在v=0.25 曲線處，平均抑制效果可達57.6%。

3） 在v∈[0.75，1.0]范圍內彈性變形預測值與實測值偏離較為明顯，導致最大預測誤差較大，準確性稍差。經過分析，其原因在于設計的輔助支撐機構在y向也即弦向的支撐位置通過螺紋孔定位，無法做到弦向支撐位置連續可調，導致第2個支撐桿位置相對理論最佳位置有一定偏離。

以上結果表明，薄壁葉片的銑削加工采用輔助支撐并對支撐布局進行優化，對于抑制葉片加工誤差，提升葉片加工精度效果十分顯著。

5 結 論

1） 綜合考慮切削過程中的材料去除以及銑削力與彈性變形的耦合效應，提出了一種薄壁葉片銑削加工彈性變形迭代預測方法，實驗結果表明，最大平均預測誤差為17.6%。

2） 采用支持向量機回歸訓練得到了葉片最大加工彈性變形以及整體彈性變形均方差的快速代理預測模型，測試結果表明回歸模型的判定系數R2接近于1，具有較高的預測準確性。

3） 建立了薄壁葉片輔助支撐布局優化模型，并基于精英策略遺傳算法和代理預測模型對葉盆型面的兩點輔助支撐布局進行了優化，實驗結果表明優化后的輔助支撐布局對于葉片加工彈性變形的抑制效果顯著，最高降幅可達57.6%。